基于支持向量机的高速滑行艇航态优化

(大连理工大学 a.船舶工程学院;b.工业装备结构分析国家重点实验室，辽宁 大连 116024)

高速滑行艇稳定滑行时，当航速过高或重心位置过于靠向船艉时，滑行艇很可能纵向运动失稳而发生“海豚运动”。在滑行艇纵向运动稳定性研究方面，主要采用Routh-Hurwitz判据法，通过计算各项水动力系数，判定滑行艇在某工况下是否会发生“海豚运动”。本文的研究目的是优化“航速-重心”组合，在保障高速滑行艇纵向运动稳定性的同时获取更佳的水动力性能。以一艘高速滑行艇为研究对象，以体积弗劳德数Fr▽及重心纵向位置lcg为设计变量进行实验设计(design of experiment，DOE)，采用经过验证的CFD计算法对样本点进行数值计算，随后引入支持向量机(SVM)法拟合各个航态之间的分界线，并提出基于“偏离度约束”的SVM，通过引入偏离度打分及距离约束改进边界的拟合方法。

1 数值计算方法及验证

为确保CFD数值计算的可靠性，需要对计算方法进行验证，流程见图1。

1.1 数值计算方法

笛卡尔坐标系中不可压缩黏性流体的控制方程包括连续性方程和动量守恒方程[1]。采用有限体积法(finite volume method，FVM)对控制方程进行空间离散求解。

(1)

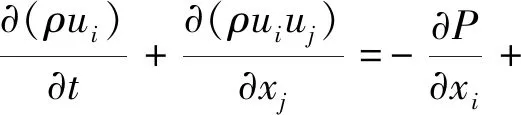
(2)

引入Realizablek-ε湍流模型使控制方程封闭可解[2]。使用壁面函数法求解壁面区域湍流发展还不充分的低雷诺数Re流动区。第一层网格距无滑移壁面的量纲一的量距离y+值应处在30～500之间。

使用多相流体积分数法(volume of fluid，VOF)对自由液面处进行捕捉，体积分数Cq可由控制方程(3)求得[3]。

(3)

采用重叠网格(overset)法将计算域划分成背景网格区域及重叠网格区域，只有重叠网格区域发生运动，大量减少了由于物体大幅运动而造成的网格加密及流域变形[4]。通过求解流体外力作用在运动刚体上的合外力及力矩(式(4)、式(5))、以及垂荡及纵摇的运动控制方程(式(6)、式(7))，获取刚体运动的新位置。

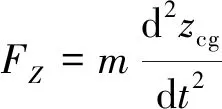
(4)

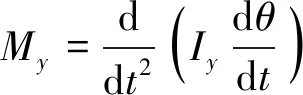
(5)

(6)

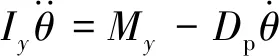
(7)

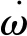
1.2 数值计算验证算例

1.2.1 计算对象

选取Fridsma系列滑行艇之一为数值计算对象，并将计算结果与公开数据进行对比[5-7]。所选滑行艇的主尺度信息见表1，型线见图2。

表1 Fridsma滑行艇主尺度及参数

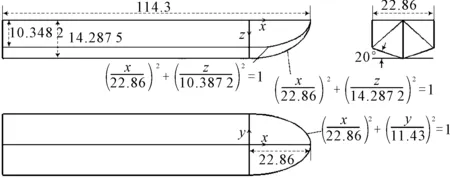
图2 Fridsma滑行艇型线

模型与数值计算均服从右手坐标系，坐标原点在尾垂线与自由液面的相交处。

1.2.2 计算域及边界条件

对于在静水中航行的船舶，其航速V与船行波波速u相等，则可根据水波理论计算其最大兴波波长λW(式8)。在不考虑流体黏性以及自由液面时，可根据伯努利方程计算最大兴波波高ZA(式9)。同时，可根据开尔文波半张角φ(约为19.47°)估算中纵剖面到船侧池壁的距离。综上所述，同时参考计算域的可视性，确定计算域的大小及边界条件的设置，见图3、4(由于滑行艇计算域尺寸较船长相比过大，为方便观察，此处用一艘低速船来解释计算域的设置)。

λW≈0.641V2

(8)

(9)

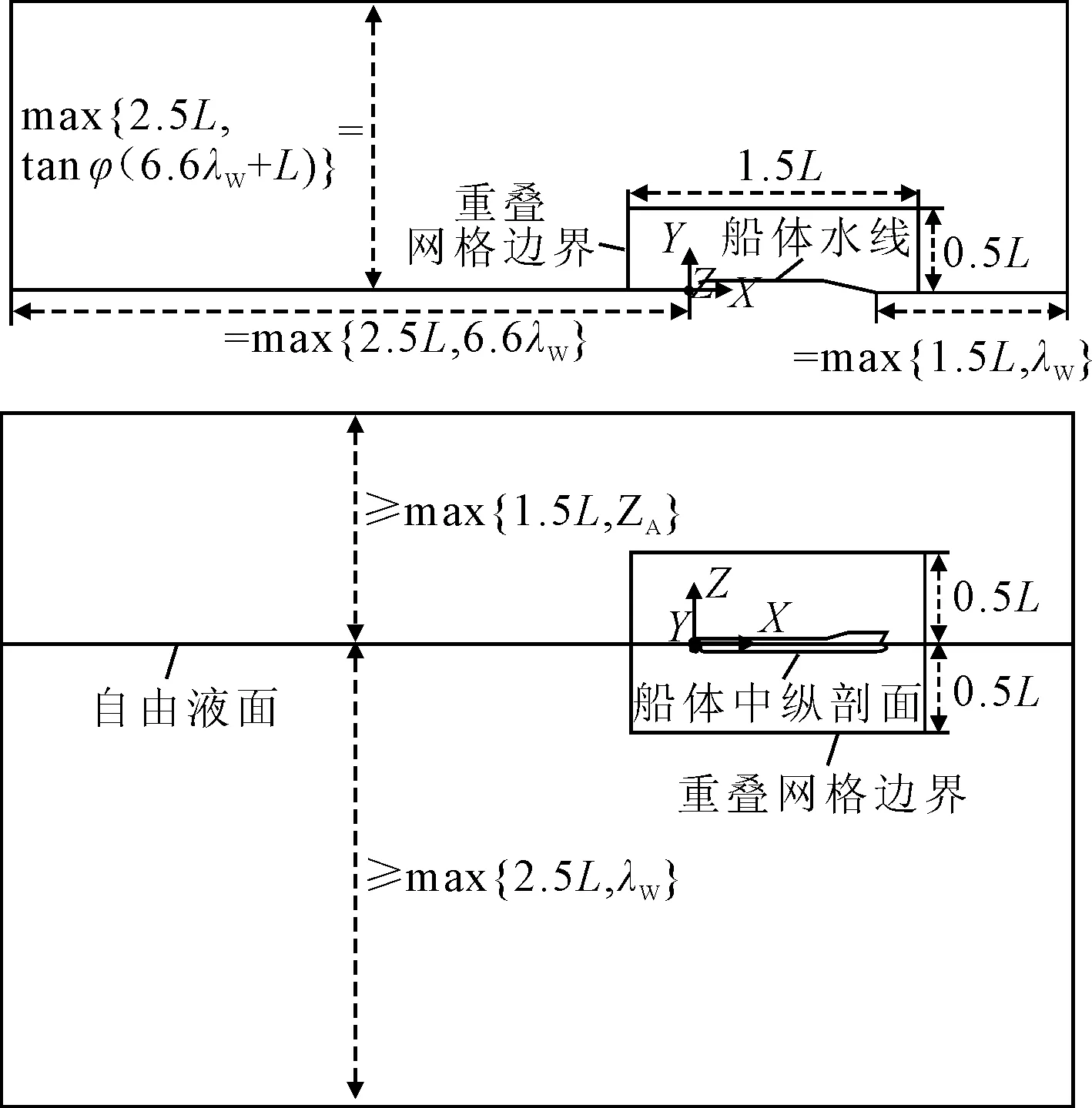
图3 计算域的确定

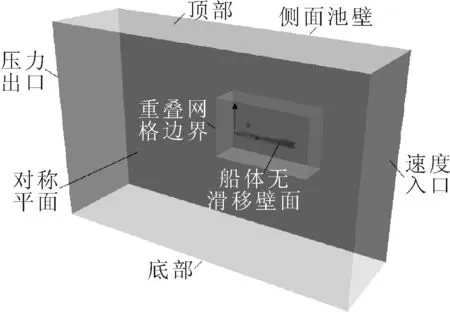
图4 边界条件

1.2.3 网格划分及网格独立性验证

采用切割体网格法对计算域进行网格划分，分别对自由液面、兴波区域、船体周围以及重叠网格区进行网格加密，在船体无滑移表面划分6层边界层，边界层区域内网格增长率为1.5，第一层网格高度Δy根据y+经验公式(10)计算[8]。

(10)

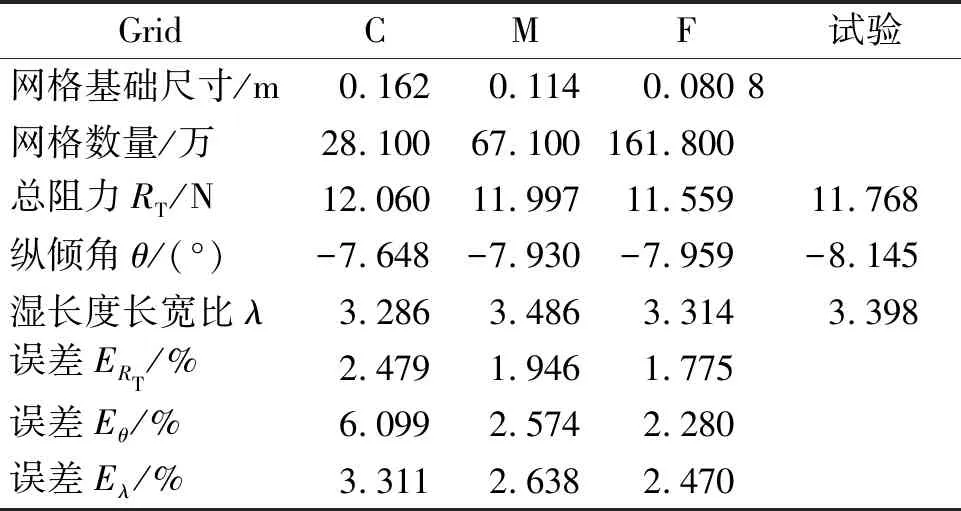
表2 网格信息及网格独立性验证计算结果

1.2.4 计算工况与验证结果

采用Grid-M对Fridsma滑行艇在Fr分别为0.595、0.892 5、1.19的3个工况进行数值计算，总阻力、纵倾，以及湿长度长宽比的计算值与试验值及文献计算值的对比情况见图5。可见采用本文提出的网格划分方式及数值计算方法可以对滑行艇总阻力及运动情况进行估算及模拟。

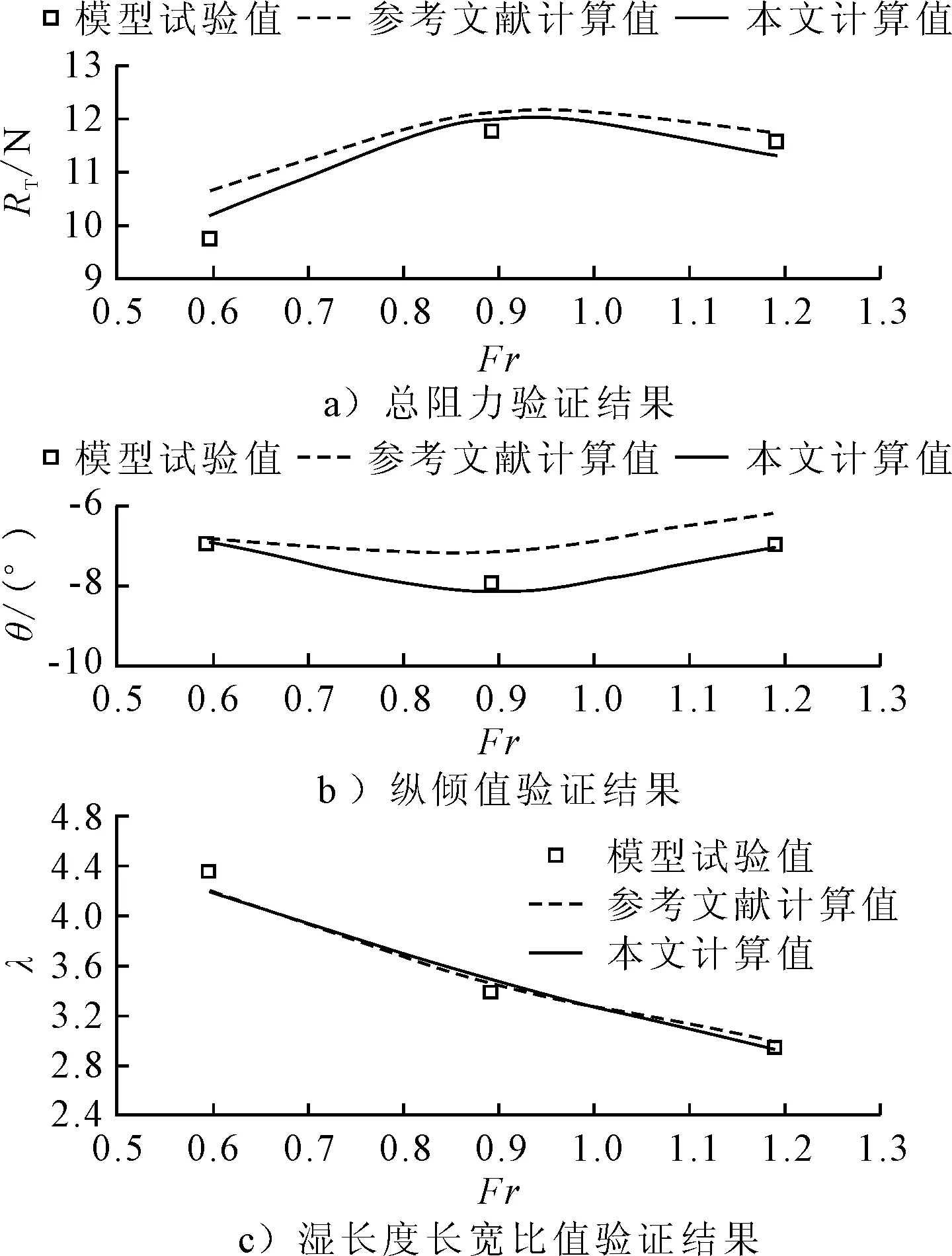
图5 Fridsma滑行艇CFD计算验证结果(β=20°)

2 高速滑行艇CFD计算

2.1 研究对象

选用由大连理工大学设计的高速滑行艇为研究对象，选取缩尺比α=2的模型进行计算。实船及模型主尺度信息见表3，三维模型见图6。

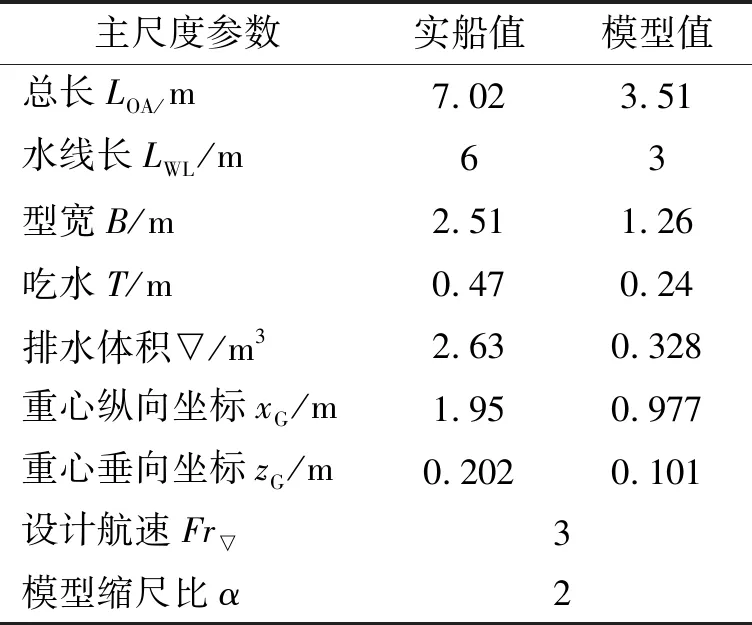
表3 高速滑行艇主尺度

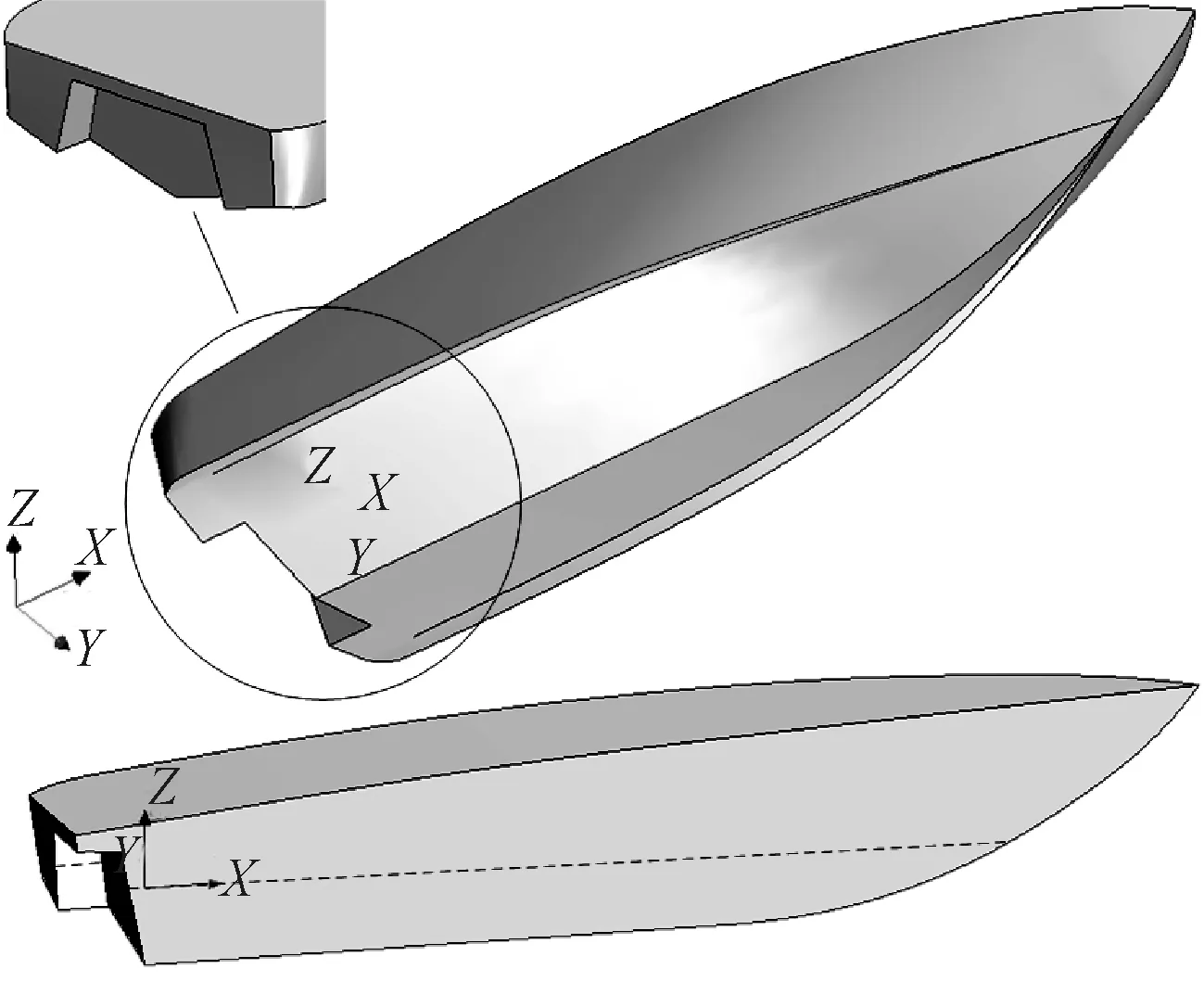
图6 高速滑行艇三维模型

2.2 数值计算

对于相同的重心位置，航速越高越容易纵向运动失稳；对于相同航速，重心位置越靠向船尾越容易纵向运动失稳。同时重心垂向坐标变化空间较小，故选取重心纵向坐标来代表重心位置。因此选取体积弗劳德数Fr▽(式(11))及重心纵向坐标xG与计算船长L之比lcg为设计变量(其中L即为LWL)。体积弗劳德数Fr▽的取值范围为[2.5,5.5]；重心纵向位置lcg的取值范围为[0.2,0.7]。使用最优拉丁超立方抽样方法(optimal latin hypercube sampling method，OLHS)[9]在设计空间选取26个样本点进行数值计算，样本点在设计空间的分布见图7。

(11)

式中：V为航速；g为重力加速度；▽为排水体积。

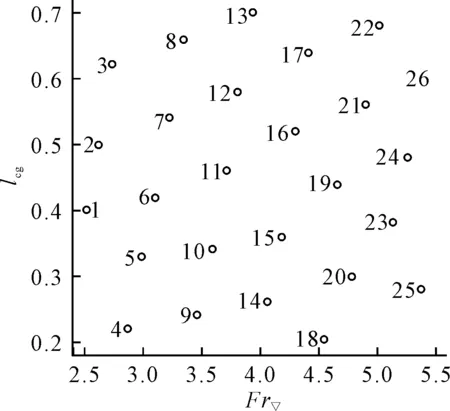
图7 高速滑行艇CFD计算样本点分布示意

2.3 数值计算结果

以样本点16为例。根据经验公式，样本点16的第一层边界层高度选取0.6 mm，预计y+值约为200。数值计算收敛结果见图8。

图8 样本点16数值计算结果

其中Sinkage为正代表船舶沿Z轴向上运动；纵倾角为负代表艉倾。计算从物理时间4 s左右开始达到平衡稳定状态，全船总阻力约为650 N。结合自由液面纵剖图(图9)及兴波图(图10)，艇身在流体动升力的作用下被抬出水面0.135 m，并艉倾2°。全船y+分布见图11，艇底y+值约为200，符合预计值。

图9 样本点16的自由液面纵剖图

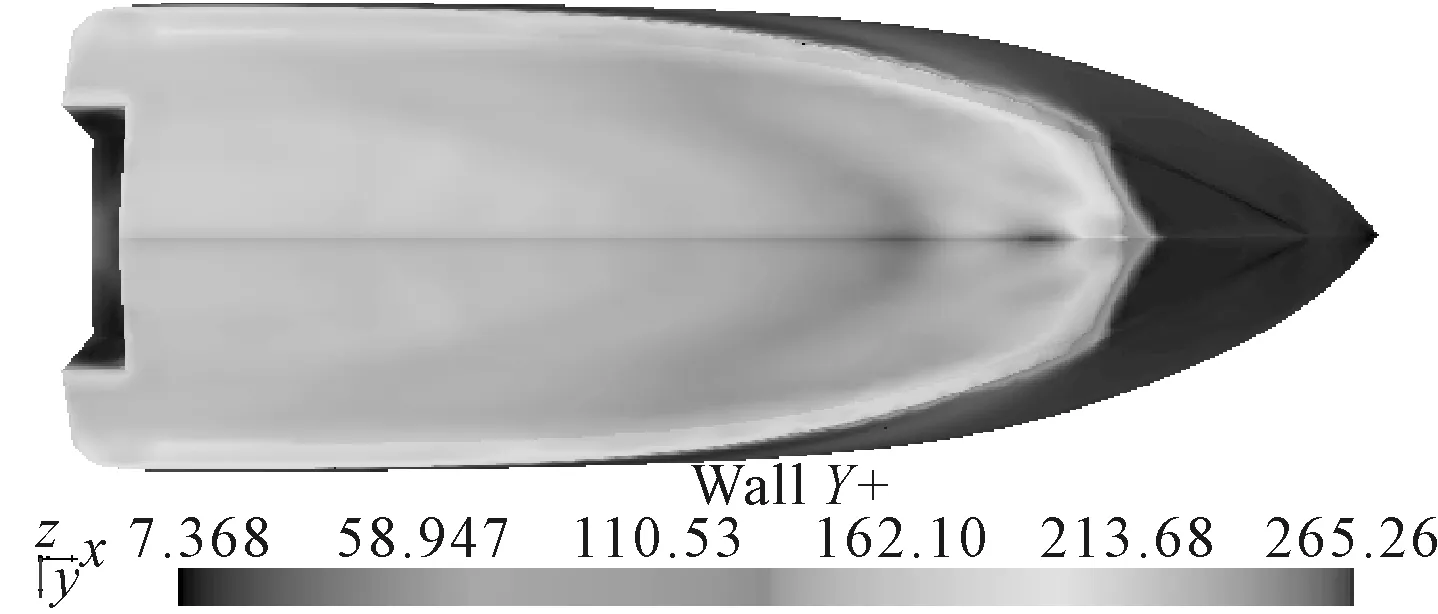
图11 样本点16的船底y+分布

3 高速滑行艇CFD计算结果及航态优化

3.1 样本点CFD计算结果

采用上述方法对全部26个样本点进行数值计算，根据对计算结果的观察，当航速相同时，可根据lcg从大到小的变化将滑行艇的航行状态分为4类。

I-排水艏倾航行(滑行艇艏倾，艇体下坐，阻力十分大，甲板或上浪，见图12)。

II-排水艉倾航行(滑行艇艉倾，艇体的一部分浸没在水中，阻力较大，见图13a))。

III-稳定滑行(滑行艇艉倾，艇体几乎完全被抬出水面，阻力大幅减小，见图13b))。

IV-纵向运动失稳(滑行艇纵向运动失稳，由于重心过于靠后，经过滑行状态后艇身飞出水面，后在重力作用下又落入水中，然后继续往复上述运动，见图14)。

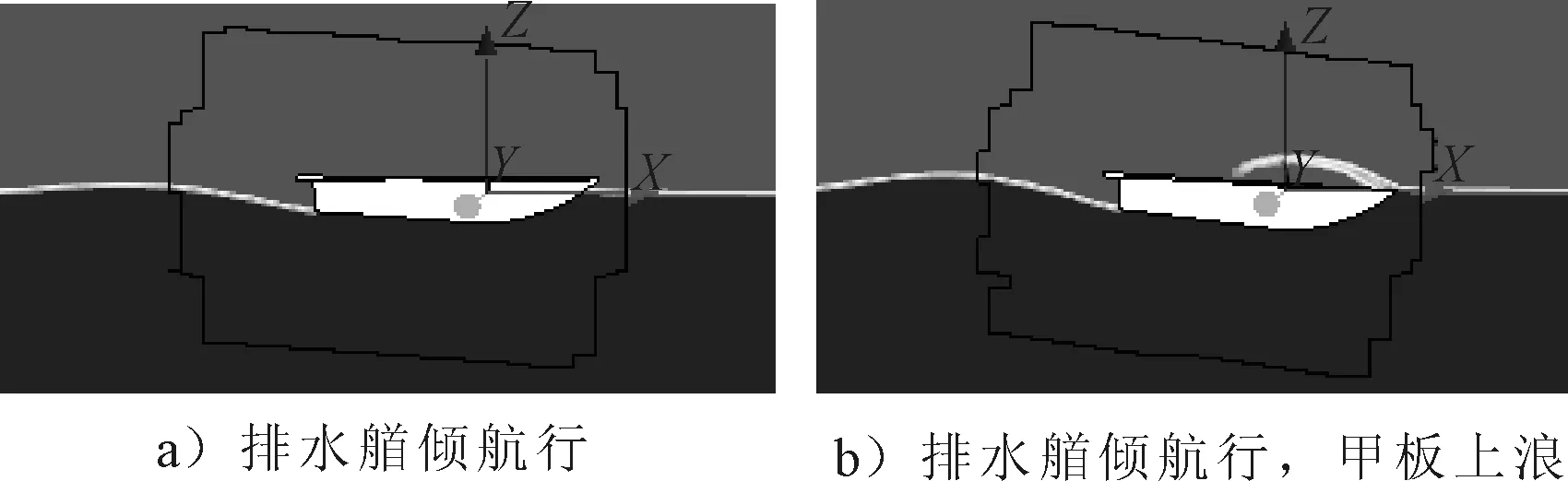
图12 航行状态I

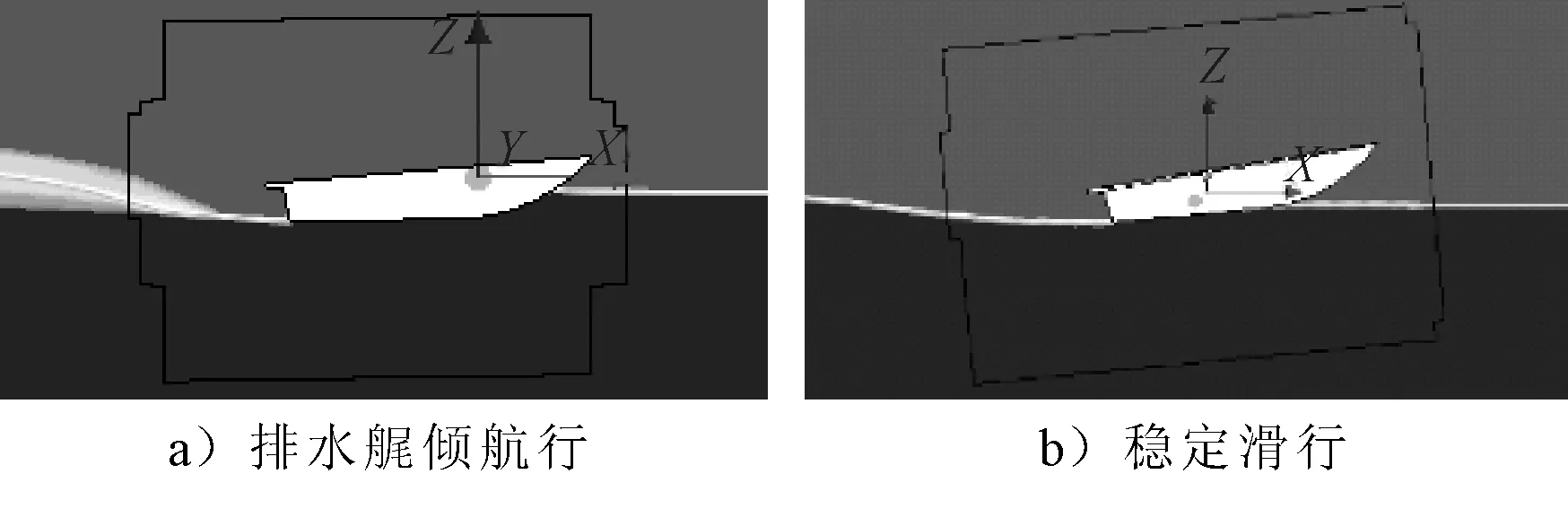
图13 航行状态II、III

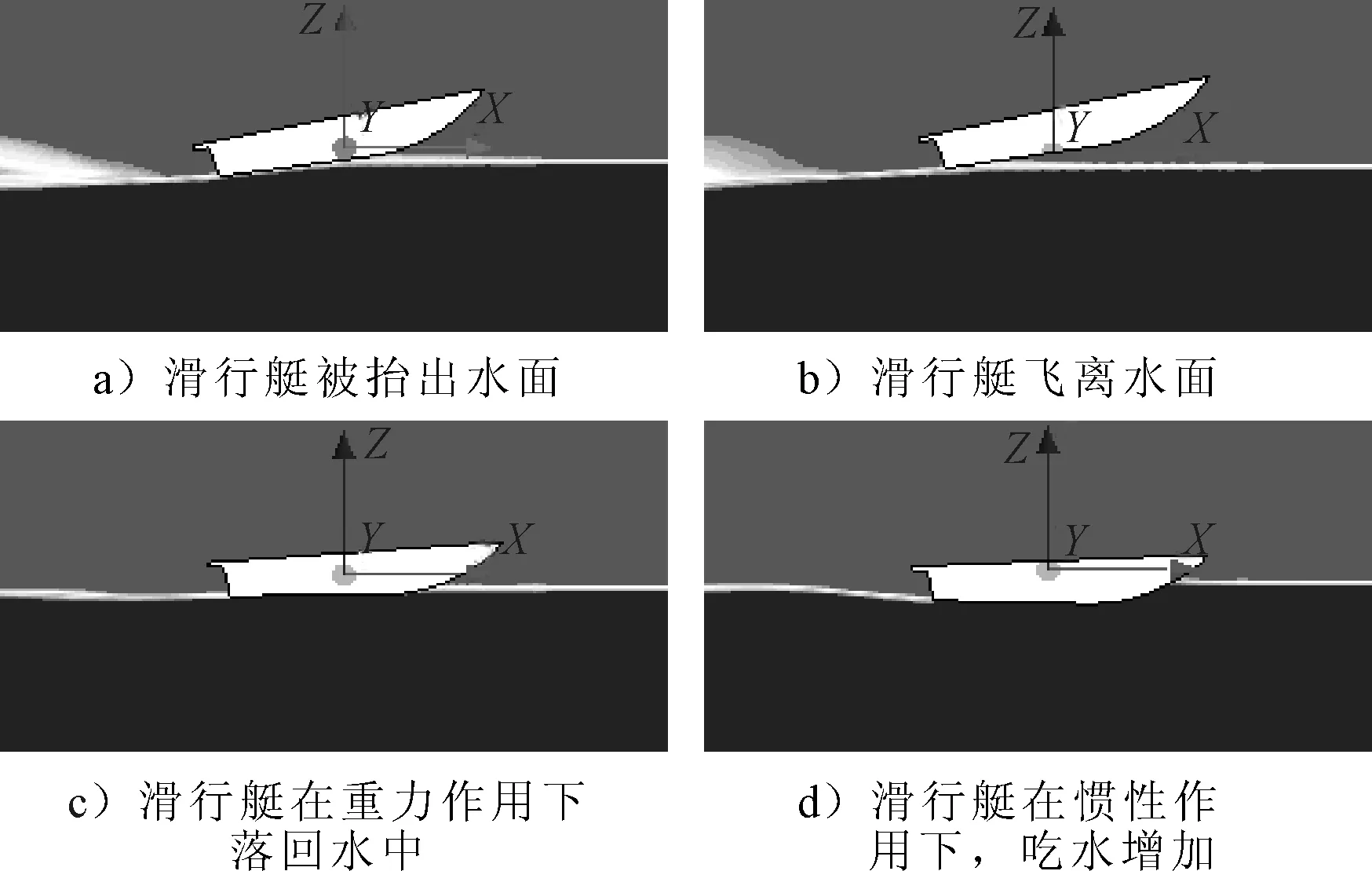
图14 航行状态IV

所有样本点的航行状态在设计空间中的分布情况见图15，其中由于处于艏倾航态的只有样本点3一个，为点3与周围样本点2、7、8之间增加加密点e1、e2与e3。

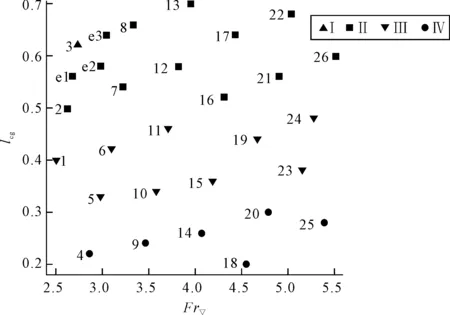
图15 样本点航态计算结果

3.2 基于SVM的航态分类

3.2.1 SVM分类原理

以样本点线性可分的情况为例，SVM的分类原理即找到一个N维最优分类超平面，在能够正确的将±1两类数据分割到超平面两侧的同时，保证两侧到该超平面距离最近的两类样本点的间隔最大化。当N=2时，超平面是一条二维直线，见图16，其中：H：ω·x+b=0为分类超平面；·为向量内积；ω为平面法向量；b为平面截距。

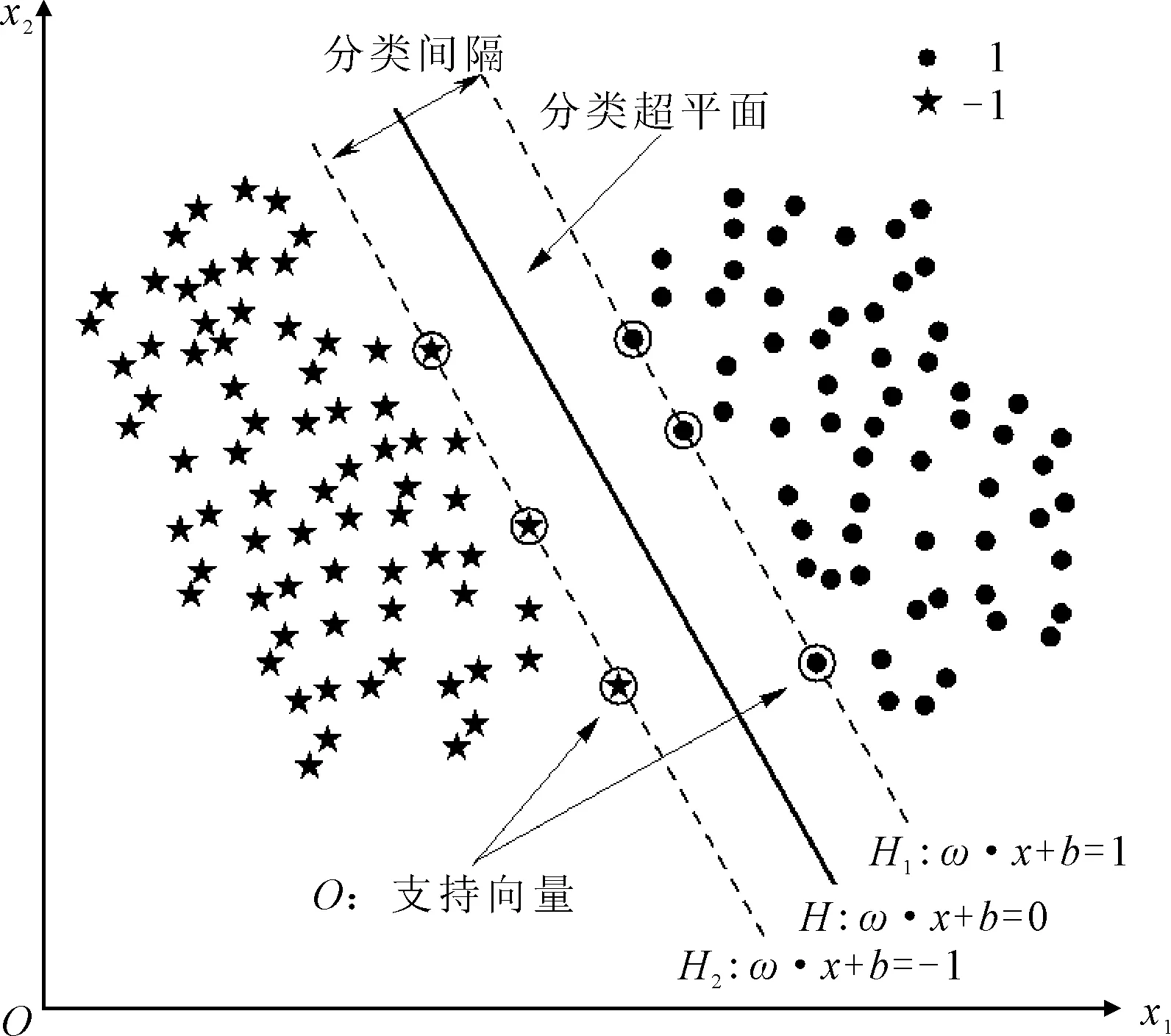
图16 最优分类超平面示意

引入Lagrange参数α=[α1,α2,…，αi,…，αn]，其中αi为每个样本点对应的Lagrange算子，将求解分类间隔最大化的优化问题转换为求解Lagrange参数向量α的优化问题(式12)。最后通过序列最小最优化算法(sequential minimal optimization，SMO)求解Lagrange参数α*。

当样本数据线性不可分时，通过引入核函数将样本数据转换到高维线性空间。

3.2.2 基于偏离度约束的SVM

将一个样本点距离最优分类超平面的远近称为偏离度。在实际计算中，即便是同一类型的数据，其偏离度也有所不同。例如，同为III型运动的样本点5与样本点23相比，更难以收敛，其运动状态更接近IV型运动，偏离度更小。然而受样本点分布的影响，在不考虑数据的偏离度时，容易出现原本应该离最优分类超平面更近的样本点反而离得更远的情况发生，为消除这种影响，在此提出基于“偏离度约束”的SVM(SVM based on deviation constraint，DC-SVM)，引入“偏离度打分”及“距离约束”。

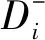
(13)

αi≥0,i=1,2,…,n+l+m-2

(14)

3.2.3 航态优化设计曲线

为指导高速滑行艇航行姿态的调整，以达到减阻提速的目的，III型与IV型航态之间的分类边界曲线C至关重要。图17中曲线A、B与C为按照基本SVM算法及二次多项式核函数拟合时的分类结果，圆圈标记的样本点为支持向量。然而分类边界曲线C的支持向量为样本点23，并不符合实际计算情况。在此使用基于偏离度约束的SVM算法，将III型运动样本点的距离约束添加到计算中，求得修改后的分类边界曲线C，此时样本点5为支持向量，各个样本点到分类边界的距离也符合偏离度排序。

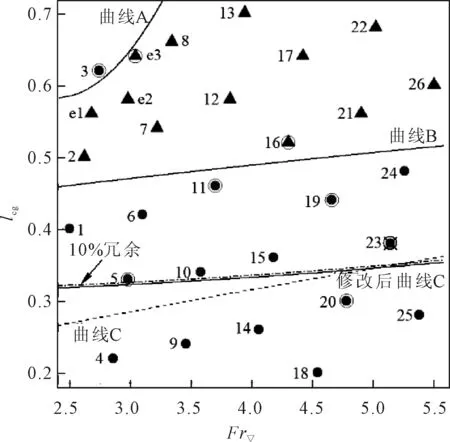
图17 样本点分类结果

由于无法直接判定处在分类边界上的设计点(Fr▽，lcg)的航态属性，需要将修改后的分类边界线曲线C向III型航态区域“推进”一定的距离，以得到相对优化的航态设计曲线。“推进”方法见图18，点P0为分界线的支持向量，点M为点P0在分界线上投影，设冗余量为c∈[0,1]，则将分界线沿向量MP0方向移动c|MP0|后，可得到带冗余度的优化航态设计曲线。当c=1时，优化分界线通过支持向量点P0，为一条保守的航态设计线；根据经验选取冗余量c=10%时，得到的带冗余的航态优化设计线。

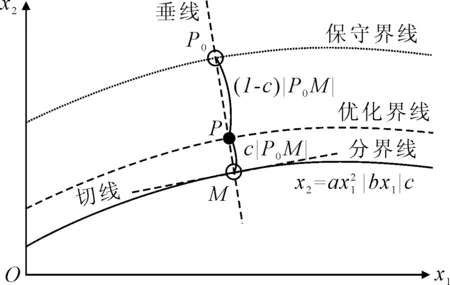
图18 分类边界、保守边界及优化边界

最终的拟合结果为式(15)～(19)。

1)分类曲线A。

(15)

2)分类曲线B。

406.83)×10-3

(16)

3)分类曲线C。

185.5)×10-3

(17)

4)基于偏离度约束的SVM求得分类曲线C。

5)带10%冗余的优化结果。

式中：x1代表Fr▽，x2代表lcg。

3.2.4 优化曲线验证

初始设计方案为Fr▽=3、lcg=0.384。由航态优化曲线(5)可知，当Fr▽=3时，优化后的重心分布lcg=0.326；当重心分布取lcg=0.384时，优化后的航速Fr▽=7.16。对初始设计点及两个优化设计点进行CFD计算，以验证航态优化曲线在减阻提速上的成果，见表4。

表4 优化结果验证

当优化设计点与原设计方案航速相同时，按照航态优化曲线的计算，将重心沿X轴向后移动5.88%，获得5.15%的减阻效果；当优化设计点与原设计方案重心位置相同时，设计航速可以大幅提升至Fr▽=7.16。

4 结论

使用具有公开试验数据的Fridsma滑行艇，验证在CFD计算中采用重叠网格法对船舶自由升沉及纵倾有较好的模拟；以体积弗劳德数Fr▽及重心纵向坐标船长比lcg为设计变量，研究高速滑行艇的纵向运动稳定性，计算结果可以较好地模拟滑行艇的4种航行姿态；采用SVM法，拟合不同航态之间的分类边界，并提出基于“偏离度约束”的SVM方法(DC-SVM)，使分类边界的计算不受样本点分布的影响，更贴近工程实际；与初始设计相比，重心优化点得到5.15%阻力降低；航速优化点的体积弗劳德数Fr▽从3提升至7.16；后续工作可以使用样本点数据，搭建近似模型，实现对高速滑行艇的阻力及纵倾角的预报。