突发事件下大规模空中交通流量管理的组合优化模型

王莉莉，王航臣

中国民航大学 天津市空管运行规划与安全技术重点实验室,天津 300300

民航局空管局近些年对“通行能力”的研究十分关注，其核心问题是可用高度层如何分配，从而达到满足交通需求、最优配置空域资源的目的。通行能力的研究体现了空域管理者对空域中运行交通流的优化调配，是空中交通流顺畅运行的重要保障。目前容量评估的理论已趋于成熟[1]，但通行能力常常达不到评估出的容量。究其原因，一方面中国空域辽阔，各地天气情况复杂多变，特点不同；另一方面，中国的两大空域用户——军航和民航在对于空域时空资源利用方面，需求存在重叠。因此有必要研究空域在危险天气与军航活动下的通行能力，从而使得军民航能够高效、公平地得以利用空域资源，达到提升空域运行效率的目的。

在空中交通流调度与通行能力的研究中，很多学者从网络流优化的角度进行建模。1992年，Helme[2]首次在空中交通流量管理(Air Traffic Flow Management,ATFM)中引入了航路容量限制约束。在时间-空间网络上使用多品种流理论(Multicommodity Flow,MCF)与最小费用流理论来解决航班的空中与地面等待问题，虽然模型简单且是连续的，但求解较为困难。2000年，Bertsimas和Patterson[3]针对文献[2]中计算时间复杂度过高的问题从另一个角度——使用动态网络流理论，构建了一个动态天气条件下延误成本最小的数学模型，并使用拉格朗日松弛与拉格朗日生成算法，将MCF问题中的难约束吸收到目标函数中，从而使模型易于求解。程朋等[4]通过动态网络流理论描述空中航路航线网络，并通过华北管制区的实际数据进行验证，该文献将机场以及与双向航路相连的管制移交点建模为一对源点和汇点，将航路段之间的中间节点视为没有流量需求和输出的导航台节点。而在实际运行中，中间节点中包括机场节点，这些节点常常有飞机起飞与降落，需要进一步的对这些节点进行刻画。2009年，赵嶷飞[5]以《图论》中的网络优化方法抽象了空中交通网络，建立了短期ATFM的动态网络流模型，首次提出了流量控制事件的概念。Odoni等[6-7]结合整数规划的方法，以扇区容量、机场节点容量和扇区连接度等因素为约束，并以欧洲空域作为算例进行仿真。2014年，Nosedal等[8]针对ATFM计算规模大、计算耗时长所造成的诸如危险天气等突发事件对航班计划影响大的缺陷，提出了一种高效率的算法，通过调整局部的航班计划从而减少空域的延误与拥挤，提升运算效率。2016年，Kicinger等[9]将危险天气视为一种随机因素，探讨了固定机场容量在不同天气输入下的通行能力。在MCF模型的求解方面，寇玮华等[10-11]做了一系列工作，通过构建复合参数和复合指标，分别讨论了容量有差异与容量无差异下的求解方法，但设计的求解算法都是针对单目标的。

综上，已有的文献主要存在以下不足：① 将航路航线网络抽象为图后，对中间节点的刻画存在不足。一方面，如果中间节点是机场则有流量进入和流出，不能单纯的将中间节点都抽象为没有流量进出的导航台点；另一方面，通行能力受限于空中交通态势，所以中间节点不能仅包括导航台点，也需要考虑航路交叉点(如某些强制报告点)。② 只考虑了单一突发事件下的流量调配，且不能很好地反映空域航路网路的拥挤程度随时间和流量变化的特点。③ 空中交通网络与《运筹学》中高度抽象的网络及其他运输方式的网络存在明显差别，主要体现在4个方面：一是模型复杂，由于空中交通流调度是在不同高度层进行的，空中交通网络是个多层次的网络；二是缺乏成熟理论的支撑且航路网出现拥挤时产生的费用(即飞行成本)考虑的因素与其他交通网络不同[12]，为贴近民航运输的情况，在构建优化模型时需要用到网络流理论、动态规划理论等；三是数据量大，许多繁忙空域日流量过千，如中国的航路枢纽——周口(ZHO)日均流量在1 200架次以上；④ 计算复杂度高，许多空中交通网络的建模是非线性的[12]，求解算法很难找到多项式时间的解，如何在可接受的时间求得符合要求的解，也是空中交通网络流优化的难点之一。

针对前面提到的4点不足，做出了以下改进。

1)针对第①点，将存在交叉的航路点都考虑进中间节点中，并将中间节点分成有流量进出的节点(机场节点)和无流量需求的节点，对有流量进出且具有中间节点性质的点进行拆分处理：分为3个子节点，分别是作为源发出流量的节点，作为汇接收流量的节点，以及转运流量的中间节点。并分别对源节点和汇节点进行建模，刻画了两种节点空域出现拥挤时的空中等待与地面等待。

2)针对第②点，建立了多目标规划模型，将航空危险天气和军航活动都考虑入模型中。

3)针对第③点，使用MCF对空中交通网络进行建模，将多高度层抽象为两节点间的多条边，通过费用函数动态反映航路相对拥挤程度，并通过设计近似算法降低算法求解的时间复杂度，从而满足流量调配的时间约束。

1 突发事件下交通流量管理的问题描述

1.1 空域的数学描述

由于中国空域现行的高度层配备原则是“东单西双”，所以可以将中国的空域网路抽象为连通有向图G=(V,E,S，Costij)[13]，其中：V为机场、导航台点和航路交叉点的集合;E为航路和航线的集合;S为扇区集合，飞机经过的扇区Sf∈S；Costij为两点间的费用。

但空域网络与网络流理论中高度抽象的网络不同，有许多自己的特点，如拥挤程度随流量变化，中间的机场节点有流量进出，存在高度层变化，空中与地面等待需要在网络中进行刻画等。

1)航路和航线

每一段航路和航线都可以用有向弧表示，如图1表示节点i,j之间的双向航路。由于拥挤程度(随流量变化情况)和可靠程度(随危险天气变化情况)不同，各航路的费用会存在差别，所以这是一个费用有差异的问题。

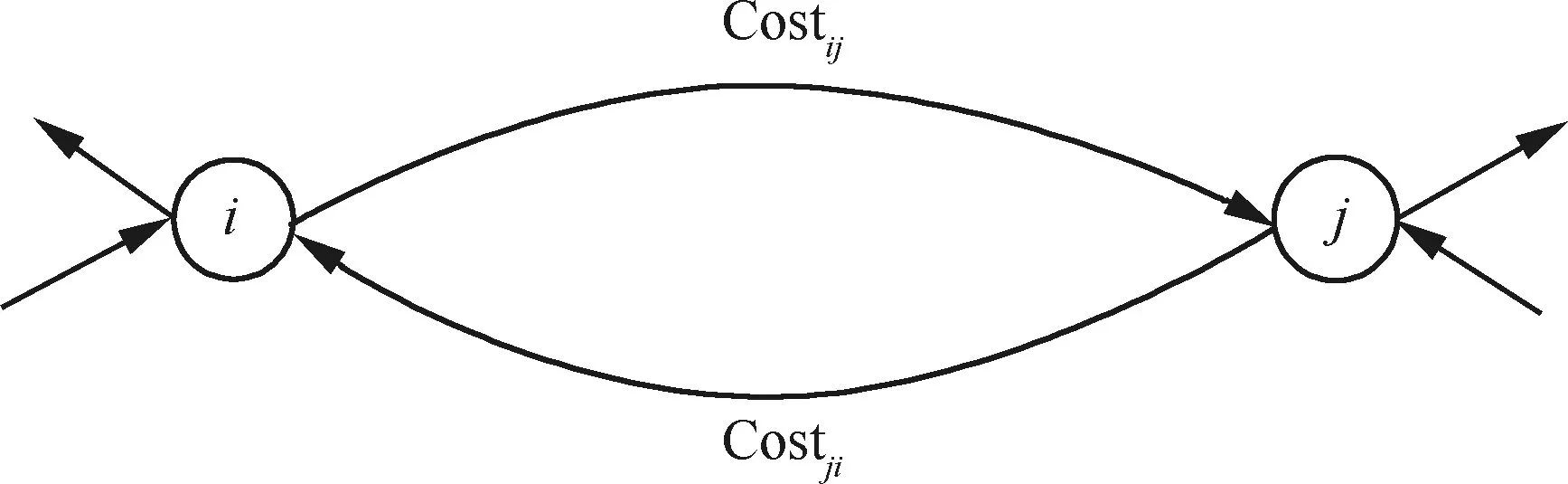
图1 航路和航线的抽象描述Fig.1 Abstract description of air route and air way

2)机场节点和航路交叉点

文献[4]将航空网络中节点分为源节点、汇节点和中间节点。在实际的管制运行中，中间节点中的机场节点有流量发出和进入的情况普遍存在，这类情况用简单的源、汇和中间节点概括会使得模型不满足实际运行的要求，同时也会违背流量守恒约束，因此有必要对中间节点进行划分。本文划分为有流量需求的中间节点Ea∈E和无流量需求的转运节点Enav∈E。这种划分能够去除文献[4]中假设2，即“正常情况下飞行流量从源点传送到汇点的过程中总流量值没有损耗”。

除此之外，航路的容量受限于航路交叉汇聚情况和空中交通态势，所以建模时中间节点的选取的节点不再仅是文献[4]中的导航台点，还包括航路交叉点(如某些具有交叉和汇聚的强制报告点)。

机场节点是有流量进出的中间节点，但很多机场节点又具有中间节点的性质，不能简单地使用拓扑结构进行抽象。故可根据以上特点，将机场节点分为3个子节点，分别是作为源发出流量的节点，作为汇接收流量的节点，以及中间节点转运流量。原理如图2所示，将有流量进出的机场节点A拆成了源节点A1、中间节点A2和汇节点A3。

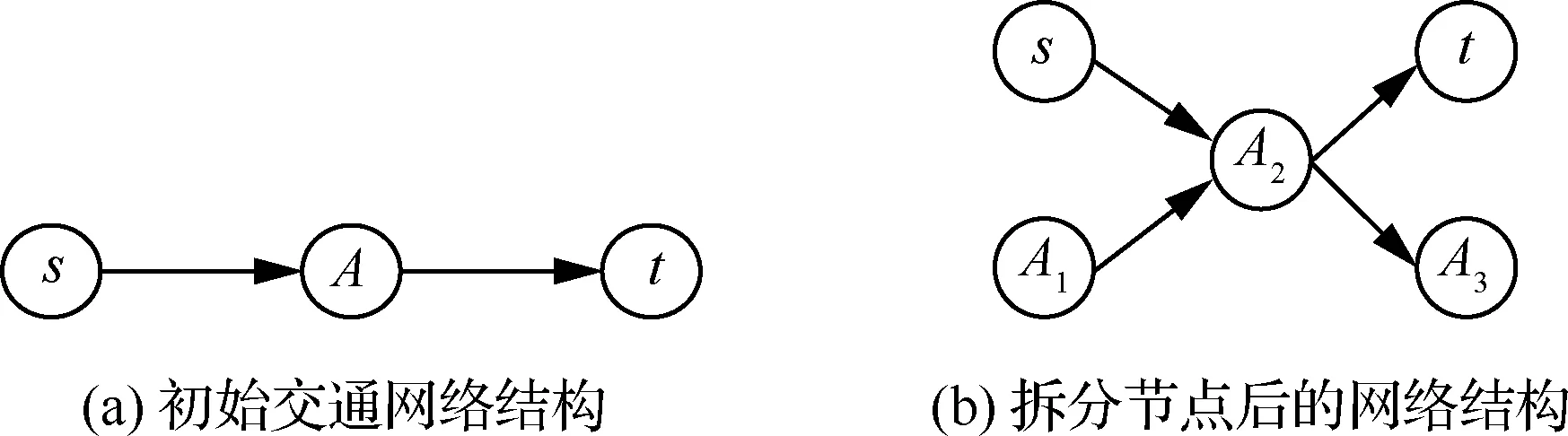
图2 有流量需求节点的处理Fig.2 Processing of traffic demand nodes

无流量需求的中间节点满足流量守恒约束，不需要做特殊处理。对于多起讫点与拆分后造成的多起讫点可以使用《运筹学》中的经典方法，添加虚拟节点转化为单起讫点问题。

3)高度层

文献[5]将同一航路上m个不同高度层的航路抽象成网络图中m条边，原理如图3所示。本文使用同样的方法构建航路航线网络的高度层。

4)空中与地面等待

在空域发生严重拥堵时，飞机抵达机场，而机场容量不足，将会出现飞机在空中的盘旋等待。通过推迟飞机起飞时间，将成本较高、风险较大的空中等待(Air Holding,AH)转变为地面等待(Ground Holding,GH)，是短期ATFM中常用的策略[14]。无论是空中还是地面等待，都会发生在机场节点，故可将源节点与汇节点做进一步的细化。原理如图4所示，由于2)中已将网络中所有节点拆分成源节点、汇节点和中间点，所以可以分别对其进行建模。源节点只存在离场交通流，若不存在延误，可以直接由节点i至节点j；若存在拥挤，需要进行地面等待，则从i至GH，再进入节点j。同理，对于汇节点，若可以直接降落，则从节点i到节点j，若需要空中等待，则从节点i至节点AH，再至节点j。

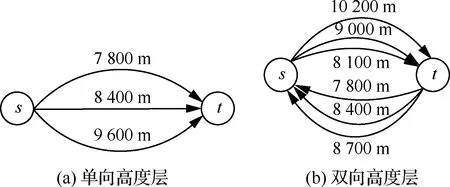
图3 不同高度层航路的简化表示Fig.3 Representation of routes at different height levels

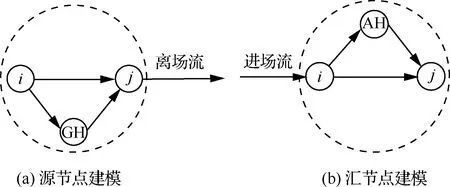
图4 机场模型Fig.4 Airport model

5)机型差异问题

跑道上前后机型组合的不同会对跑道的容量和安全间隔产生影响，本文将机型划分为大型机(H)、中型机(M)和小型机(S)来计算机型成本，3种 机型对机场节点的影响差别较大，有必要针对以前的研究中将空中交通流视为一种流的假设做出改进，使用MCF分别描述3种机型。

由于仪表间隔的限制，任一时间各机场节点能降落和起飞的飞机数量都是有限制的，机型的分布对这些机场节点的通行能力有较大的影响，为了描述这一问题，建模时应考虑机型分布的影响。机型分布建模中，由于到达某机场的飞机机型是随机分布的，可采用离散概率分布建模。用大型机、中型机和小型机占所有航班计划的百分比，表示该机型到达的概率，设空中交通流中大型机、中型机和小型机所占百分比分别为p1、p2和p3，且p1+p2+p3=1。

1.2 ATFM中航路航线选择的费用问题

经典运筹学方法在研究流量分配时，将交通网络理想化，即假设网络上不存在阻塞现象，每条边的费用固定，这种假定适用于小流量下的交通网络，但对于大流量且存在阻塞现象的交通网络，计算的结果不符合一线运行。在实际的管制运行中，∀i,j∈V,航路航线的费用Costij随着流量的增加递增，管制员分配流量时也会在“多条航路和航线”之间权衡选择。影响管制员路径选择的因素主要有航路航线的运行费用(衡量各时段流量变化带来的影响)、空中与地面等待的成本、危险天气带来的影响和军航活动。

1.2.1 航路航线运行费用

由于国内外文献缺少对航空网络“拥挤程度”的定义，所以引入“相对拥挤”这一概念来平衡和分配空中交通流量，即在向最小费用的通路分配流量后，其路径费用会由于新增流量而不再是最小的，下一次迭代要重新衡量“相对拥挤”的程度。文献[15]首次针对航路和航线的费用函数进行建模，本文使用相同的费用函数来表示航路航线网络“相对拥挤”的程度变化情况：

(1)

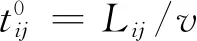
除了航路航线的费用，由1.1节中所述，航路航线网络中的机场节点还存在AH节点与GH节点，对于两种等待也应赋予费用函数。在空域出现拥挤时，通过比较从源节点到汇节点的总费用与地面等待、空中等待的费用，从而决定是否采用地面等待策略。AH每单位时间的成本远比GH的高，假设每架航空器的延误应该是“平等的”。因此，可在目标函数引入成本系数ε，使之变为一个略微超线性函数。引入成本系数将有利于航班延误分配的适度性与公平性，从而不会出现延误分配严重不均的情况。空中等待亦然，引入空中等待的成本系数ε2，并令其大于地面等待系数ε1，从而实现AH每单位时间的成本远比GH的高的约定。引入两个参数的原因是使目标函数进行近似变换，整体考虑空中等待与地面等待，从而克服Lulli和Odoni(2007年)提到的流量管理模型“公平性不足”的问题[6]。

(2)

式中：TDf=AHf+GHf为航班f的总延误。

如果目标函数仅表示为最小化AH与GH之和，则与已有文献分开考虑并计算AH与GH没有区别。经过式(2)的变换，目标函数考虑到了总延误TD。使用总延误作为目标函数不仅具有能够有效区别空中等待与地面等待费用的优点，还能够克服引言中提到的大多数模型将空中延误费用和地面延误费用分开计算的缺陷，这样设置目标函数求得的结果是从系统的角度进行考虑的，充分地考虑了两者之间的相互影响。

综上，等待费用由两部分组成，第1部分考虑航班的总延误，第2部分则是起飞前采用地面等待所节省的费用。故针对每个时刻t，设af为航班f的计划到达时间，df为航班f的计划离场时间，定义下述费用系数：

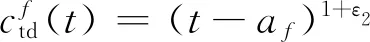
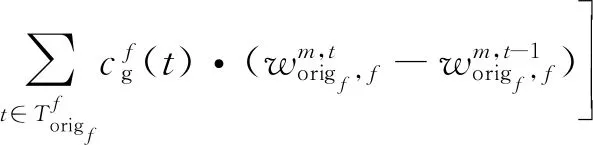
(3)

(4)

1.2.2 突发事件费用

1)危险天气

1.2.1节中的费用函数没有考虑天气因素带来的可靠性变化。天气是对民航运输影响最大的因素之一，表现在终端区航空器进离场受到延误和航班取消等、空域扇区内航空器为避开危险天气改航，从而导致航路通行能力降低。为了给空中交通网络流提供最可靠的路径，需要考虑航路和机场节点两个方面的重要度。

衡量路径可靠性主要有两种准则：链条准则和串联准则[18]。两种准则表现在航路网络中有不同的意义：在链条准则下，如果航路都经过某一机场节点，并且它的可靠度在航路集合的所有节点中是最低的，则这些航路具有同样的可靠度，故以链条准则表示航路可靠度难以区分各航路的差别；而在串联准则下，考虑到连接航路的各机场节点对航路可靠性都有影响，则能以可靠度串联的乘积形式表现出各航路的区别。为了描述航空危险天气的随机性，航路的可靠度可定义为

(5)

式中：RPa为整条航路a的可靠度；Rij为航路(i-j)∈Pa的可靠度，Pa表示由源节点到汇节点的一条由航路组成的通路。为了便于求解，可将式(5)两边取以e为底的对数，得

(6)

若以-lnRij作为中间机场节点(i-j)费用的一部分，则可将天气因素考虑到实际运行中。

2)军航活动

随着中国国防建设与民航事业的持续发展，军民航防撞的任务日益艰巨，军航活动对于民航飞行与空管保障会带来一系列影响，如部分航路航线的关闭、民用机场短时禁航、改变民用飞机计划航路和航线等。军航活动与危险天气带来的影响不同，危险天气会造成通行能力的下降问题，但军航活动会造成一切飞行活动的避让，一旦发生，将会出现部分节点和航路航线不可使用的问题。所以在建模过程中，军航活动不体现在费用函数上，而是体现在最短路径的选择上。

在对各航路进行配流时，需要先迭代计算最小费用，搜索最短路，所以军航活动带来的影响具体可以表征为

情况1计划最短航路航线时，必须飞越某节点。

情况2计划最短航路航线时，不能飞越某节点。

情况3计划最短航路航线时，必须经过某节点但不能经过某节点。

情况4计划最短航路航线时，经过某节点就不能经过另一节点。

情况5计划最短航路航线时，经过某节点就必须经过另一节点。

综上所述，在搜索最小费用的航路分配流量时，需要充分考虑这些因素，从而得到军航活动下民航飞机的调度方案。

2 短期流量管理模型

短期流量管理模型中的变量如表1所示。

表1 模型中所用变量Table 1 Parameters in model

2.1 目标函数

短期流量管理的目标通常是使空中等待与地面等待的损失成本总和最小，但由于实际管制运行中出于安全和成本考虑，只将地面等待作为目标函数。但由1.2节的分析，航路的费用、空中等待与地面等待的费用和危险天气带来的费用都需要考虑，有多于一个要追求最优的目标。

第1个优化目标是使航路网络总费用最小，可表述为各航路费用之和最小，则优化目标可表示为

(7)

式中：为了区分飞行任务的重要程度，引入一个非0的权重系数λm，大型机活动的重要系数大于1，中型机和小型机的重要系数小于1。

第2个优化目标是使空中等待与地面等待的成本最小。目标函数可写为

min:Zh(x)=CostH

(8)

第3个目标是使危险天气对航路航线网络的影响最小，即飞行计划与调度飞机时路线的可靠性最好，可表示为

(9)

2.2 约束条件

1)机场的进离场容量约束

不同的跑道使用策略下机场容量不同，机场的进离场约束可表示为

(10)

(11)

式(10)表示时刻t起飞的航空器架次小于机场的离场容量，式(11)表示时刻t起飞的航空器架次小于机场的进场容量。跑道容量的确定方法在很多文献里已有详细的介绍，如文献[19]，在此不再赘述。

2)扇区容量约束

文献[4]的容量约束是航路容量约束，但空中交通与地面交通不同，空中交通航路/航线的容量是以扇区为单元表述，故可将容量约束表述为扇区容量约束：

(12)

虽然表述改为扇区容量约束，但第1个目标函数，即式(7)中需要使用各航路流量衡量费用函数的变化。可表示为

(13)

3)航班的连续性约束

(14)

(15)

(16)

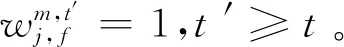
4)扇区的连续性约束

(17)

(18)

(19)

式(17)～式(19)表明扇区的连接性，式(17)约定一架航空器如果截至时刻t-lfj′j没有抵达扇区j之前的某一扇区，那么截至时刻t，航空器也无法到达扇区j；式(18)和式(19)对航空器到达扇区的时间做了约束。

5)非负与整数约束

(20)

截至t时刻，空中交通流量是一个非负整数变量，即

(21)

3 求解算法设计

3.1 算法设计思路

在求解MCF这一问题上，经典算法主要有拉格朗日松弛法、列生成法和Dantzig-Wolfe分解等，其他常用的算法还有将MCF问题视为容量指派问题[20]。这些算法面临的一个重要问题是算法求解的时间复杂度高，而短期ATFM的时间敏感度高，在大流量的调度问题上难以满足短期ATFM的需要。前面提到的文献不能满足上文中提到的网络费用随时间和流量变化的特点，也不能准确描述军航活动给网络带来的影响。

由于危险天气具有随机性，各地气象台能对危险天气做出概率预测，故以其为输入数据之一；航路费用随流量的变化而改变，而流量又有明显的时变性，故各时段的流量也是输入数据之一；一切飞行活动都要避让军航活动，所以军航活动会造成部分点和边不可用，本文通过修改最短路算法来描述军航活动带来的影响。

3.2 军航活动下的最短路算法

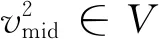
对于情况3，是情况1和情况2的组合。

对于情况4，主要包含3个过程：第1个过程是将G转变为不包含经过某节点的新图，搜索其最短路；第2个过程是将G转变为不包含不能经过某节点的新图，计算出必须经过某节点的最短路径；第3过程是对两个求解出的最短路取最小。

对于情况5，主要包含3个过程：第1个过程是将G转变为不包含经过某节点的新图，计算其最短路径；第2个过程是对G计算出起点到经过某节点的最短路，计算出经过某节点到必须经过某节点的最短路径和必须经过某节点到终点的最短路径，再将3个最短路合并；第3个过程对比第1和第2过程，取其小。

3.3 模型的求解算法

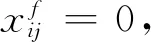
步骤2更新费用。将分配得到的流量加载进航路网络，根据流量分配结果更新式(1)的费用，根据气象报文MATAR更新式(6)的费用，从而得到新的航路费用。

步骤3判断是否有军航活动。如有则进行步骤4，否则进行步骤5。

步骤4根据3.2节中情况，调用对应的改进Dijkstran，n=1,2,3,4,5，计算最短路。

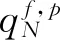
步骤7列出目标列表。建表过程参见文献[21]。

步骤8给定初始约束集。令x1=x。

步骤9计算权系数δp。

步骤10求解辅助问题，辅助问题的构造参见文献[21]，可得辅助问题的最优解(xp,λp)。

若对所有目标均满意，则输出Z*=ZM。

若对所有目标都不满意，或M=3时仍有一些目标不满意，则无满意解，停止迭代。

若M<3，对目标Z表示满意，进行步骤12。

步骤12由管制单位根据天气与空域拥挤程度，给出最大宽容量，作新的约束集合。

4 仿真算例

将西南空管局所管制的空域作为算例对模型与算法的可行性和求解效率进行分析。先以2016年11月28日的实际数据为例进行初步验证。仿真选取该区域的6个机场节点，包括成都双流机场(ZUUU)、重庆江北机场(ZUCK)、绵阳南郊机场(ZUMY)、昆明长水机场(ZPPP)和丽江三义机场(ZPLJ)和贵阳龙阳堡机场(ZUGY)。该空域除了机场，包含23个扇区，973条边，88个节点(没有交叉的不计入)，日均流量超过300架次的繁忙节点有10个，如图5所示。这些节点对网络的通行能力有较大影响，应重点分析。

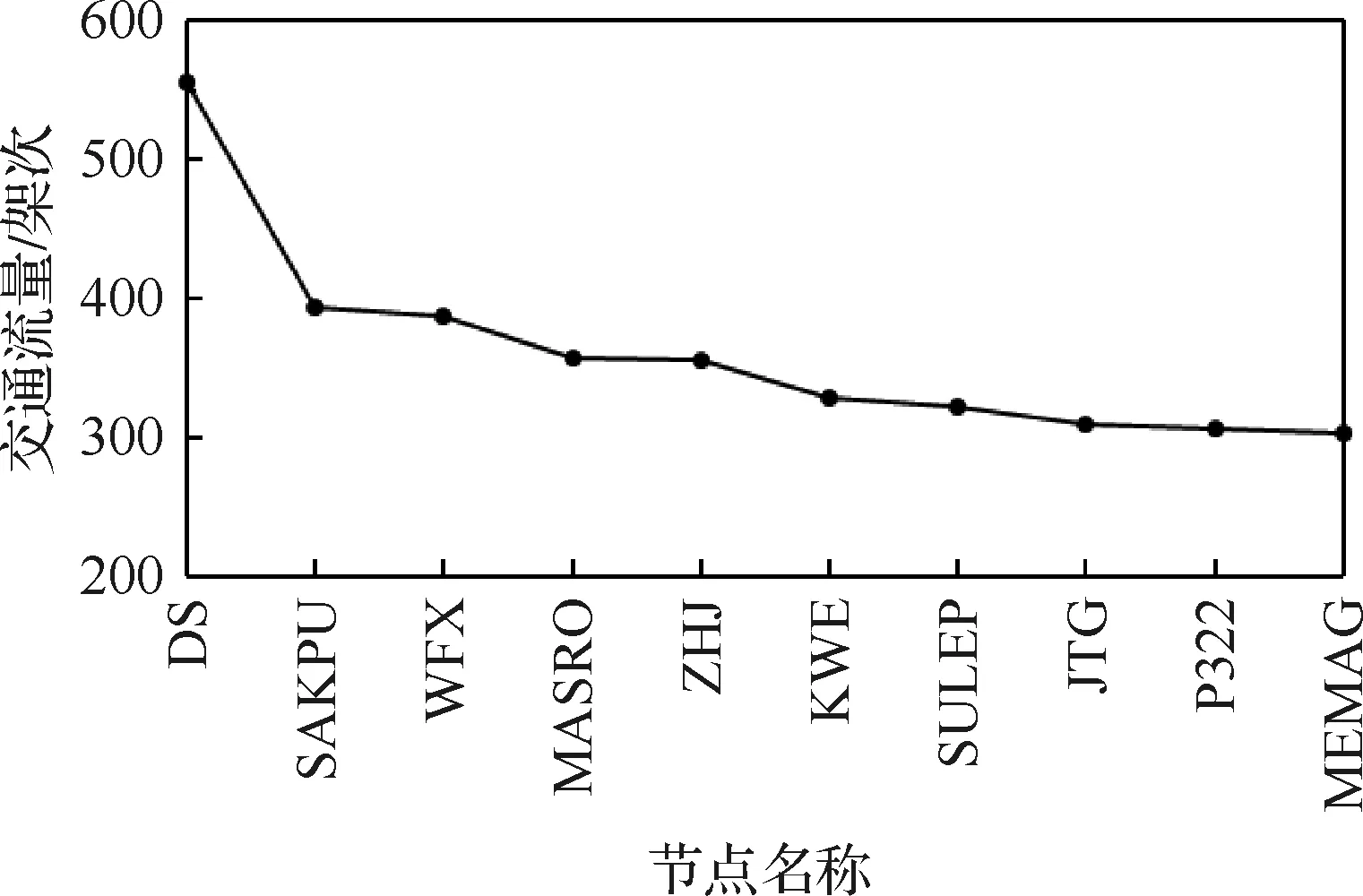
图5 流量超过300架次的节点Fig.5 Nodes with more than 300 flights

为了验证不同情况下模型的运算效果，分别构建3种不同的场景进行仿真。

场景1西南地区空域不受天气和军航活动影响，正常运行，即所有路径可靠度均为1，没有节点禁航。

场景2由于航空危险天气的出现，导致通行能力下降，将扇区的通行能力分为5档，即20%、40%、60%、80%和100%，分别计算不同通行能力下模型对AH与GH的分配，气象条件见参数设定段。

场景3由于军航活动的出现，导致部分节点短时间禁航，分别选取大流量节点(日均300架次以上)和小流量节点(100架次以下)，在考虑天气影响的情况下，分析不同流量级别节点禁航下对网络通行能力的影响。时间采样以min为单位。

模型参数具体设定为，在可接受离场延误为 15 min、进场延误为10 min时，设各个扇区的容量均为10架次，ZUUU和ZUCK高峰小时保障架次为40架，其他机场均为25架，流的品种数m=3。为了模拟气象条件的动态变化，使用计算机生成随时间变化的气象信息，且其在同一时间窗内不发生变化，在实际的运行可根据该地区历史天气数据进行标定，设3种机型进近着陆所占的比例分别为40%、35%和25%。

1)场景1的实现与验证

任何一个ATFM模型的重要原则都是保证延误分配的公平性[7]，但过于保证公平性会导致系统运行效率的降低。本文提出的引入参数ε1和ε2从来整体考虑到总延误TD，能有效克服这一矛盾。模型中使用的目标函数，其略微超线性的成本系数和对于总延误的考虑，使得模型可以相对均匀地分配延误，从而避免大量延误“堆积”，由后续航班承担的情况，从而保证了模型的公平性。

作为说明，图6比较了延误的分配。横坐标表示受影响的航班编号，按延误时间(纵轴)升序排列。实线表示本文设定的目标函数分配得到的延误，虚线段表示GH与AH简单线性求和作为目标函数时延误的分配。可见，考虑总延误时，受影响的31架航空器延误可以更加均匀地进行分配。

在完成实际数据初步验证后，通过改变输入流量，验证固定容量但不同的通行能力下的仿真。

2)场景2的实现与验证

由表2可知，两个机场每架飞机的平均延误随着通行能力的下降，逐渐升高。但由于模型中将空中等待的成本设置的比地面等待成本高很多，故在延误分配中，地面等待分配的时间也高于空中等待。

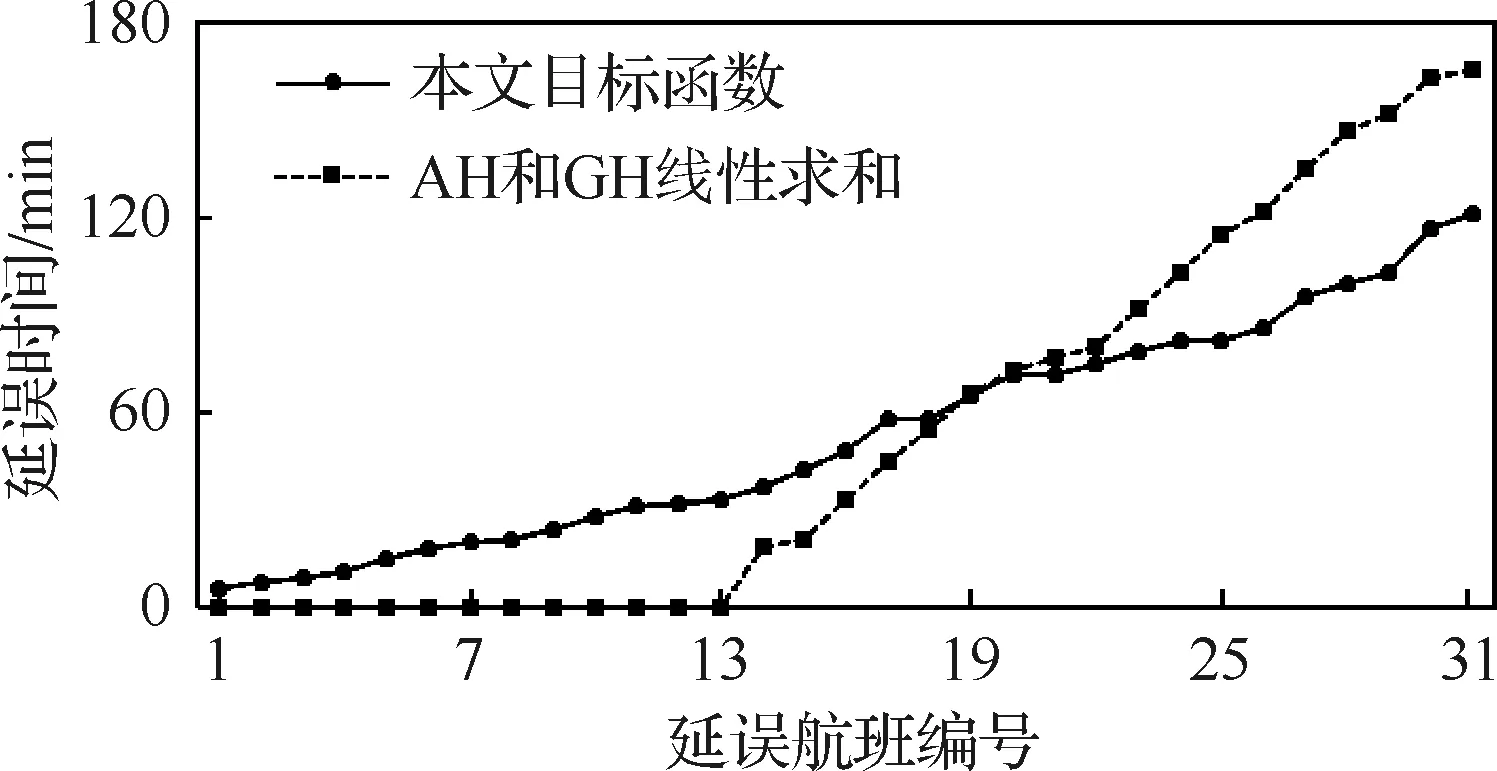
图6 延误分配Fig.6 Delay distributions

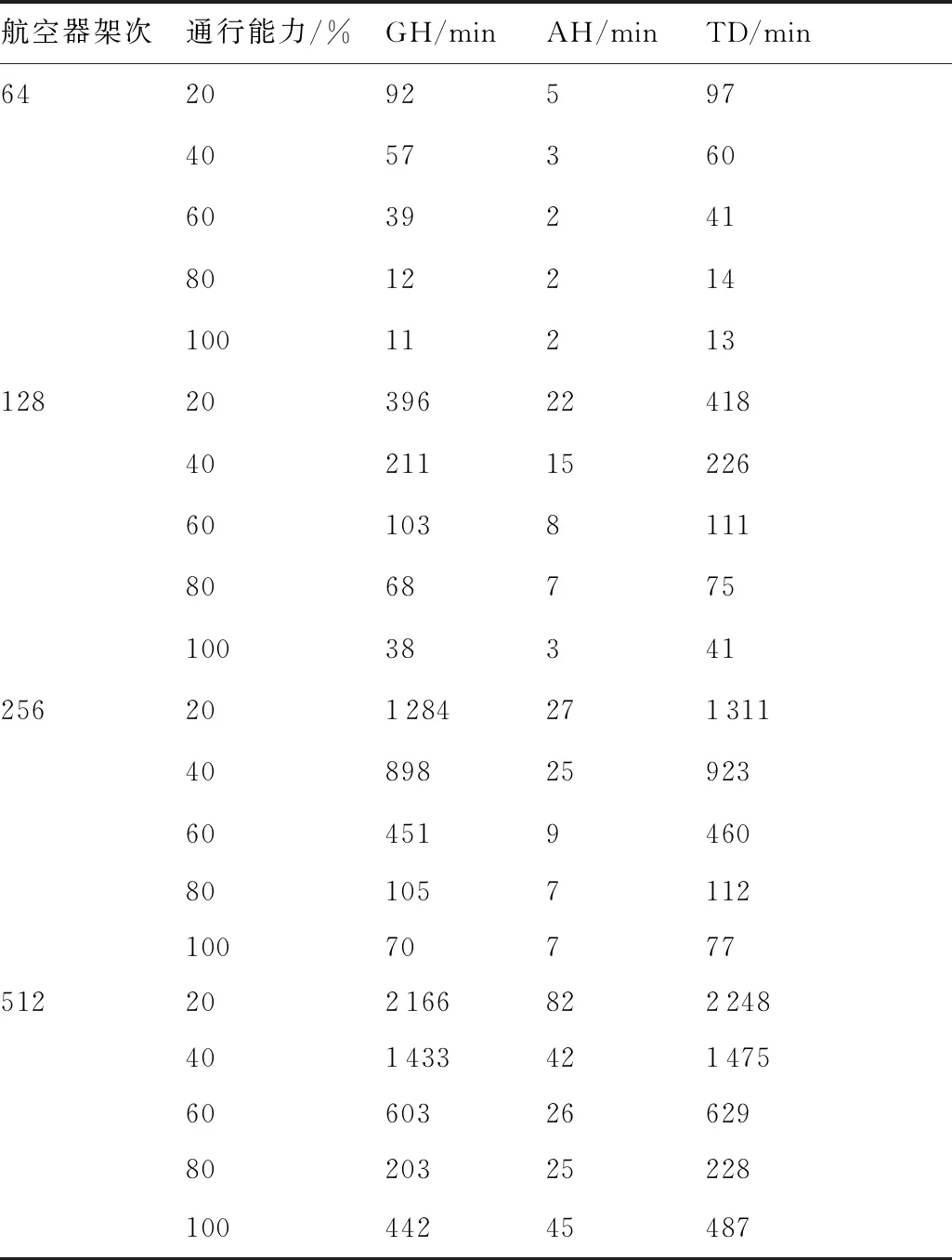
表2 延误分配结果Table 2 Results of delay assignment

如果按照传统方法，简单的将AH与GH线性求和作为目标函数，将延误飞机的延误时间按升序排列后，会出现类似图7的结果，出现延误的“堆积”，这一点流量越大越明显。以大流量低通行能力进行分析，即512架次与1 024架次，通行能力20%为例，如图7所示，如果以传统的AH与GH简单线性求和作为目标函数，后续的航班的等待时间较长，这将导致大量航班取消。以240 min为限，超过此时限航空公司需要向乘客支付延误补偿。可见，相比于以往很多文献将AH与GH加权求和，所提目标函数能均匀地分配延误，提升流量调配的公平性。

图7 延误超过240 min的飞机数量对比Fig.7 Numbers of aircraft delayed more than 240 min

在算法效率方面，通过CPLEX软件求解模型，算法运行环境为1台CPU为Intel Core i5-4590 3.30 GHz*2，4 GB内存的台式计算机。在算例给出的空域结构下进行仿真，短期ATFM时间敏感度高，要求在短时间内得到可靠解。算例设置的总求解时间长度为120 min，流量管理阶段的时间窗为0～120 min，通过求解的时间与迭代次数对本文提出的算法与经典算法进行比较，分别将其他几种算法与逐步宽容算法相结合。

由于列生成算法和Dantzig-Wolfe分解算法通常针对的是单目标而且有特殊结构的优化问题，故仅在算法步骤5中使用这两种算法求解第一个目标函数，且令λf=0，列生成算法以最短路算法为子问题。运算结果见表3。

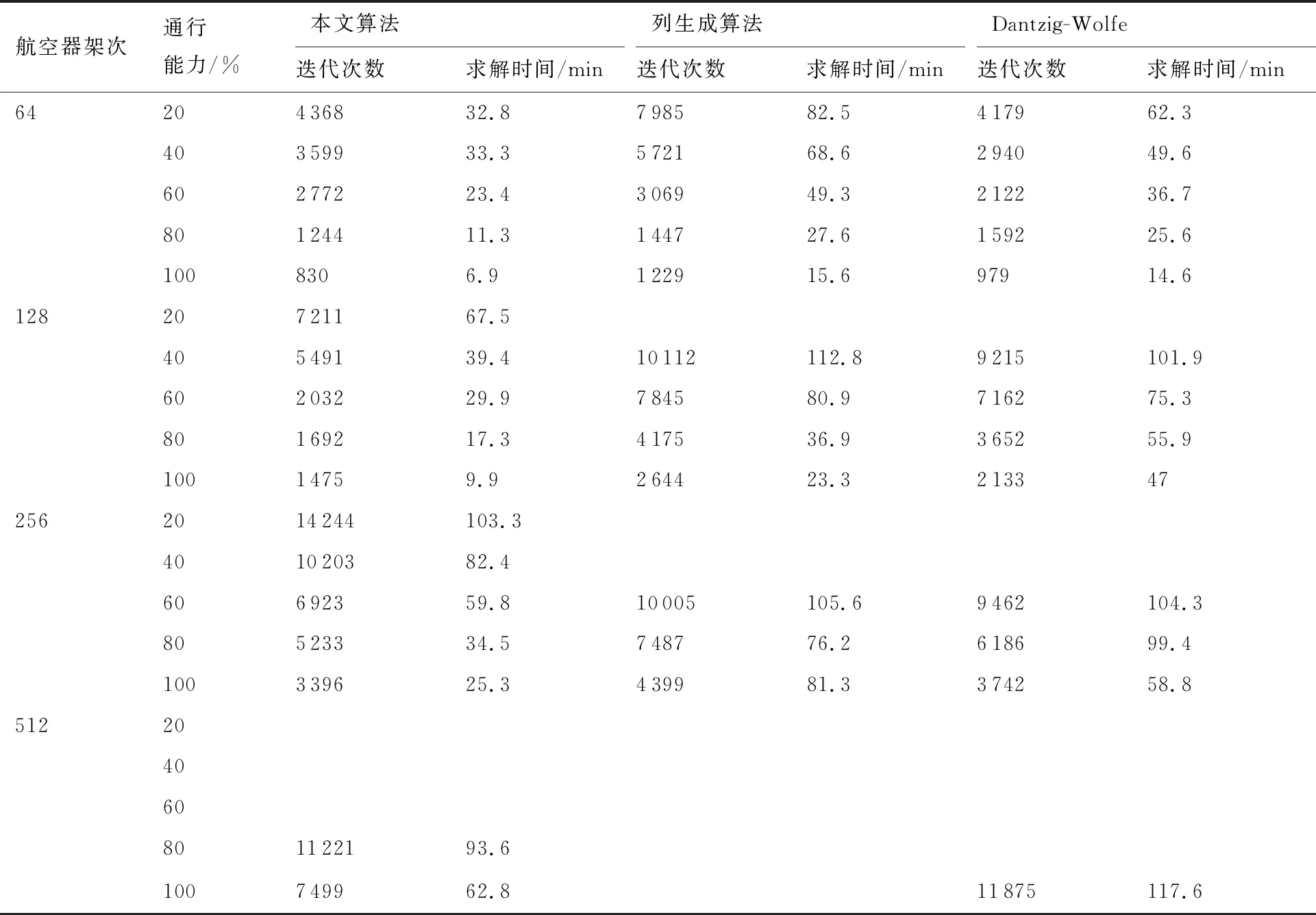
表3 算法求解性能分析Table 3 Algorithm performance analysis

3)场景3的实现与验证

由图5可知，算例空域的关键节点有10个，这10个关键节点有不同的特点。主要分为以下2种情况。

1)大流量节点和小流量节点相邻，MASRO和KHP就属于这种情况，其中MASRO的日流量达到357架次，而KHP的日流量只有58架次。

2)大流量和大流量节点相邻，如WFX和JTG，两者日流量均在300架次以上。

前文提到的参数w表示飞机是否经过某一航路，也可以之判断飞机是否改航。以MASRO、KHP、WFX和JTG为例，使用改航的飞机数来衡量这两种情况对航空网络运行造成的影响。如图8所示，当大-大流量节点相邻时，一旦节点禁航，改航的飞机数最多；大-小节点相邻大节点禁航次之，小节点禁航改航的飞机最少。

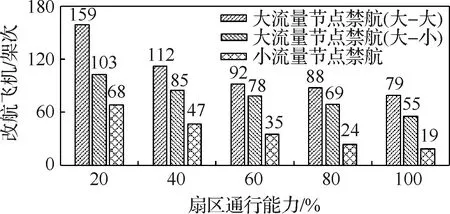
图8 不同关键节点造成的改航飞机数Fig.8 Number of aircraft rerouting caused by different key nodes

5 结 论

根据中国民航管制运行特点，对容量与通行能力的概念进行了界定，并使用MCF理论，建立了突发事件下空中交通流调度的动态网络流模型，并针对多品种动态网络流模型求解时间复杂度高的特点，改进了逐步宽容约束法，设计了一种阶段式求解的逐步宽容算法。

在模型建立方面，通过引入0-1变量衡量航路网的连通程度与航空器的改航问题；考虑了大型机、中型机与小型机交通流的尾流差异，将飞机性能问题转变为一个MCF问题，并对各品种流量引入权重系数，从而在优化中体现优先大型机活动、保障中型机正常运行的宗旨。在目标函数方面，针对危险天气的随机性、网络拥挤程度随流量和时间变化的特点、空中等待和地面等待建立了多目标规划模型；在约束条件方面，考虑了机场容量、航路容量和时间上的连接性。

在模型求解方面，针对军航活动的特点，改进了最短路算法，针对传统算法求解MCF时间复杂度高的问题，改进了逐步宽容约束法，提出一种阶段式求解的近似算法。

算例结果表明，所改进的模型与提出的算法能够在危险天气和军航活动下，高效地求解多品种流下大规模空中交通流量分配问题，相比于传统算法在大流量下更具效率优势。优化的效率与结果更符合航路网络的运行特点。

致 谢

感谢崔德光教授，作者从崔老师处获益良多。