反向交叉眼对单脉冲雷达干扰效果分析及仿真验证

周亮，孟进，吴灏，刘永才，刘伟

海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033

导弹是飞机、舰船等作战平台生存的重要威胁，目前导弹末端跟踪制导主要以单脉冲雷达为主。由于导弹使用频率低、使用时间极短，平时搜集积累的信号特征数据少，使得导弹末端防御成为当前作战平台自我防御的重难点。

交叉眼干扰被认为是对单脉冲雷达最有效的干扰方式之一[1-3]。随着数字射频存储器(Digital Radio Frequency Memory，DRFM)技术的出现，交叉眼干扰工程实现成为可能，对此，国内外学者对交叉眼干扰进行建模并展开了大量的研究。文献[4]对交叉眼干扰角度欺骗的有效性进行了暗室实验证明。文献[5-6]对不考虑目标回波下的交叉眼干扰进行了建模，对交叉眼干扰和反向交叉眼干扰在单脉冲雷达和差通道特征差异进行了分析；文献[7]对考虑平台回波和隔离平台回波的情况，分别研究了两点源反向交叉眼干扰对幅值比、相位差的参数容限。针对两点源反向交叉眼干扰参数苛刻的问题，不少学者对两点源交叉眼干扰为基本干扰单元进行组阵，具体研究为：文献[8-10]对正交旋转反向交叉眼干扰下单脉冲雷达指示角进行推导，研究了正交旋转反向交叉眼干扰的参数容限；文献[11-13]分别对考虑平台回波和隔离平台回波下的线性阵反向交叉眼干扰机参数容限展开了研究;文献[14-15]对多源环形阵反向交叉眼干扰的参数容限展开了研究。文献[16]针对多点源反向交叉眼干扰基线长度差异引起相位误差而抵消其宽松的参数容限问题，对相位补偿方法展开了研究。文献[17-18]对交叉眼干扰收发天线阵的互易性设计展开了研究。文献[19]从雷达天线极化的角度对减轻交叉眼干扰进行了研究。综上所述：当前研究主要集中于反向交叉眼干扰苛刻的幅值比和相位差等参数容限问题，较少对干扰机天线间距、雷达与干扰机距离以及干扰机相对雷达的转角等参数变化对干扰效果的影响进行研究，且未从单脉冲雷达信息处理的角度对模型的正确性进行分析。

依据国外交叉眼干扰技术应用于电子战装备的相关文献[20-21]，交叉眼干扰与距离波门拖引干扰结合使用，使得交叉眼干扰为隔离平台回波下的场景使用，从而形成较为稳定的欺骗角。对此，本文以比相单脉冲雷达为干扰对象，在不考虑平台回波的情况下，基于雷达方程、单脉冲雷达测角原理，建立隔离目标回波下的两点源反向交叉眼干扰数学模型，研究了干扰机相对雷达的偏转角变化、干扰机与雷达间距离的变化、信号幅值比和相位差变化对反向交叉眼干扰效果的影响，并依据单脉冲雷达接收机角度信息处理流程，建立单脉冲雷达接收机仿真模型，对反向交叉眼数学模型的正确性和局限性进行了验证和分析。研究结果可为机载和舰载交叉眼干扰设计提供参考。

1 反向交叉眼数学建模

交叉眼干扰机一般搭载于飞机、舰船平台，保护平台不受以单脉冲雷达跟踪的精确制导武器袭击，交叉眼干扰机与单脉冲雷达的相对位置如图1所示，其反向天线结构如图2所示。单脉冲雷达在受到交叉眼干扰后，单脉冲雷达角度指向图1中黑色方块部分。图1中：θr为雷达视轴相对于干扰机中心的转角，θe为干扰机天线与雷达天线中心连线的夹角，θc为干扰平台旋转角，θ1、θ2分别为Antenna-1和Antenna-2与雷达视轴线的夹角，θs为干扰机引起的单脉冲雷达测角误差大小，r1为雷达中心至干扰机天线1的距离，r2为雷达中心至干扰机天线2的距离,x为Antenna-1到干扰机天线与雷达天线中心连线的垂直距离，y为Antenna-1到干扰机天线与雷达天线中心连线的垂直点与其中心点的距离，r为干扰机天线与雷达天线中心连线的距离，dp为雷达孔径距离，d0为干扰机天线与雷达天线中心连线点到假目标的距离。图2中：dc为干扰机天线之间的间距，J1、J2分别为干扰机的两发射天线,R1、R2分别为干扰机的两接收天线,φ为改变的相位。

图1 单脉冲雷达与干扰平台的相对位置Fig.1 Relative position of monopulse radar and jamming platform

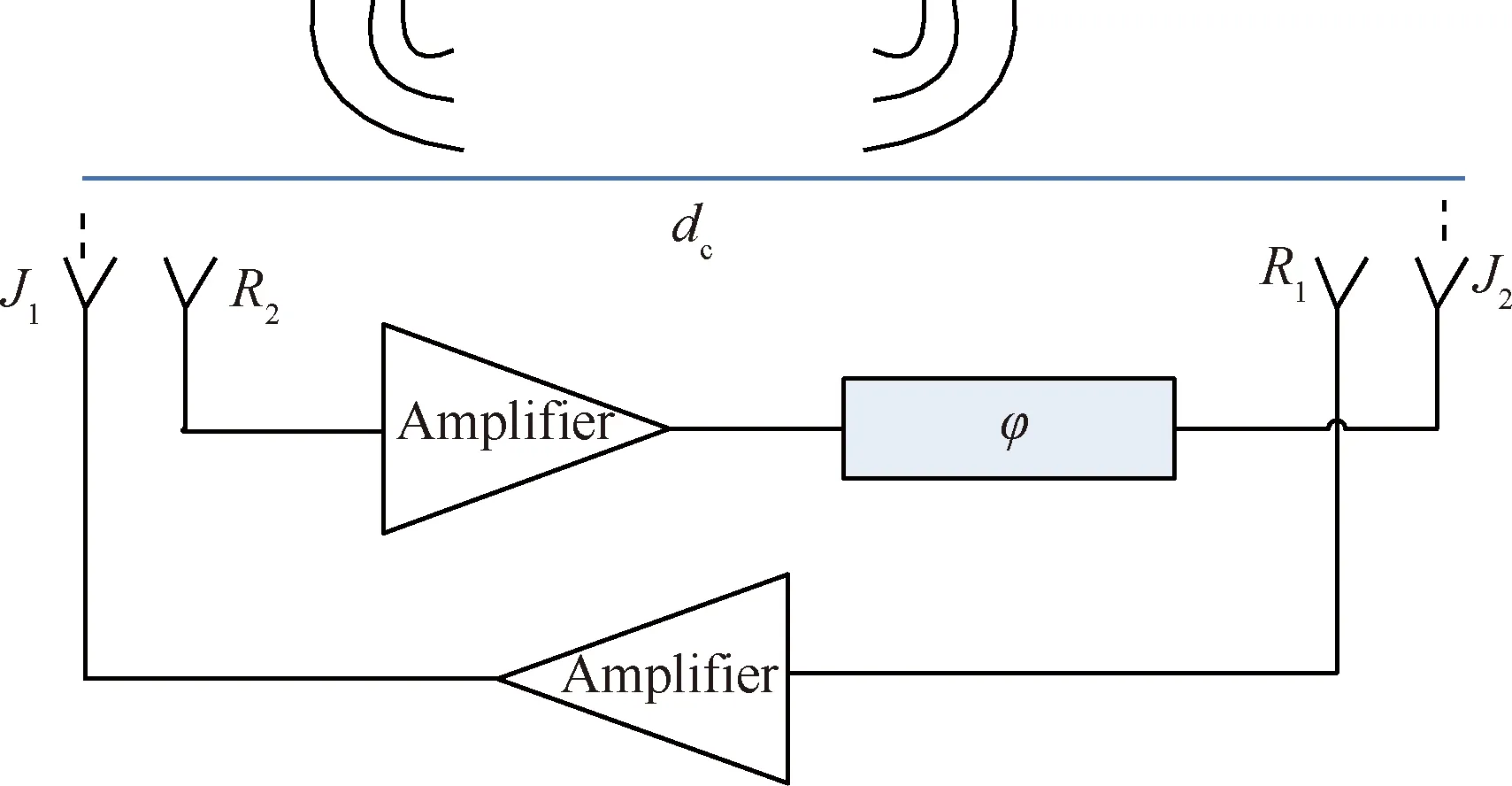
图2 交叉眼干扰机的反向天线结构Fig.2 Reverse antenna structure of cross eye jammer

假设单脉冲雷达发射的信号为ε(s)，θ1方向增益为FΣ(θ1)、在θ2方向增益为FΣ(θ2)，则依据雷达方程，干扰机接收天线R1和接收天线R2处接收到的雷达信号分别为

(1)

式中：G为单脉冲雷达发射和信号的增益；r1、r2分别为单脉冲雷达和信号达到干扰机接收天线的距离；λ为信号ε(s)对应的波长。

经过干扰机信号调制后，干扰机发射天线J1和干扰机发射天线J2发射的雷达信号分别为

(2)

式中：G1、G2分别为信号经天线R1、R2接收后至发射天线J1、J2的功率增益；L为信号经天线接收至发射的电缆长度，假设从天线R1、R2接收的信号至发射天线J1、J2的线缆长度通常保证相等。

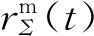
(3)

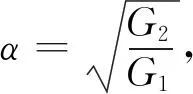
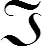
(4)

从图1得知，θ1、θ2与θr、θe之间的关系为

(5)

而根据文献[2,8]可知，单脉冲雷达的和通道与差通道增益分别为

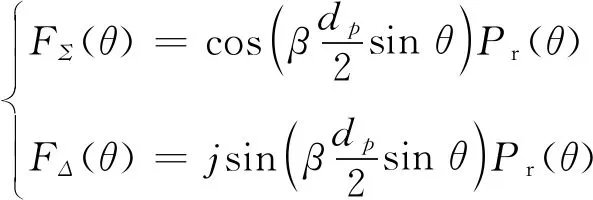
(6)

式中：β为玻尔兹曼常数，β=2π/λ；Pr(θ)为单个波束的增益方向图。

结合式(5)和式(6)，对式(4)中差信号与和信号比值进行化简，可得

(7)

依据三角积化和差公式2sinxcosy=sin(x+y)+sin(x-y)，对式(7)化简，并令

(8)

将式(8)代入式(4)，得到雷达的单脉冲比为

(9)

(10)

而依据式(6)，计算的得到的单脉冲雷达的单脉冲比为

(11)

联合式(9)～式(11),可得

(12)

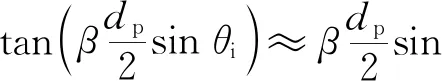
sinθi≈sinθrcosθe+Gccosθrsinθe

(13)

式(13)中三角函数中角度值均蛮小，因此可进一步简化，得到单脉冲雷达指示角为

θi≈θr+θeGc

(14)

根据图1，交叉眼干扰引起单脉冲雷达测角误差大小为

θs=θi-θr=θeGc

(15)

(16)

将式(10)和式(16)代入式(14)和式(15)可计算单脉冲雷达指示角θi、交叉眼干扰引起雷达测角误差大小θs。

2 反向交叉眼干扰效果影响因素分析及模型验证

2.1 仿真参数

以文献[22]中的反舰导弹搭载的单脉冲雷达为干扰对象，交叉眼干扰机与雷达的参数如表1所示。

表1 干扰机与雷达的参数Table 1 Parameters of jammer and radar

当干扰机与雷达相对位置固定时，根据式(14)可知，引起单脉冲雷达指示角偏差的主要因素是交叉眼干扰增益Gc和θe，Gc主要与交叉眼信号幅值和相位差相关，θe主要与R0、θc、dc等参数相关，而对交叉眼的幅值比和相位差等参数边界范围已有较多文献进行了研究，本文对影响交叉眼增益Gc和θe大小进而影响交叉眼干扰效果的相关参数进行分析和验证。

2.2 反向交叉眼干扰效果影响因素分析

2.2.1 幅值比和相位差对干扰效果影响

在干扰机两路信号幅值比α∈(0.7,1)、φ∈(160°,200°)时，采用本文数学模型计算得到单脉冲雷达测角误差θs的等高线如图3所示。

分析图3可知，幅值比越趋近于1、相位差越接近180°，θs的值越大，交叉眼角度欺骗效果越好。如当干扰机两路信号相位差为180°，干扰机发射信号幅值比分别为0.8、0.9和0.95时，θs的值分别为1°、2.3°、5°。这与文献[4]的暗室实验分析结果所得规律一致。

2.2.2 干扰平台旋转角对干扰效果影响

当干扰机两路信号幅值比为0.95、相位差为180°时，干扰机引起的雷达测角误差随转角变化如图4所示。

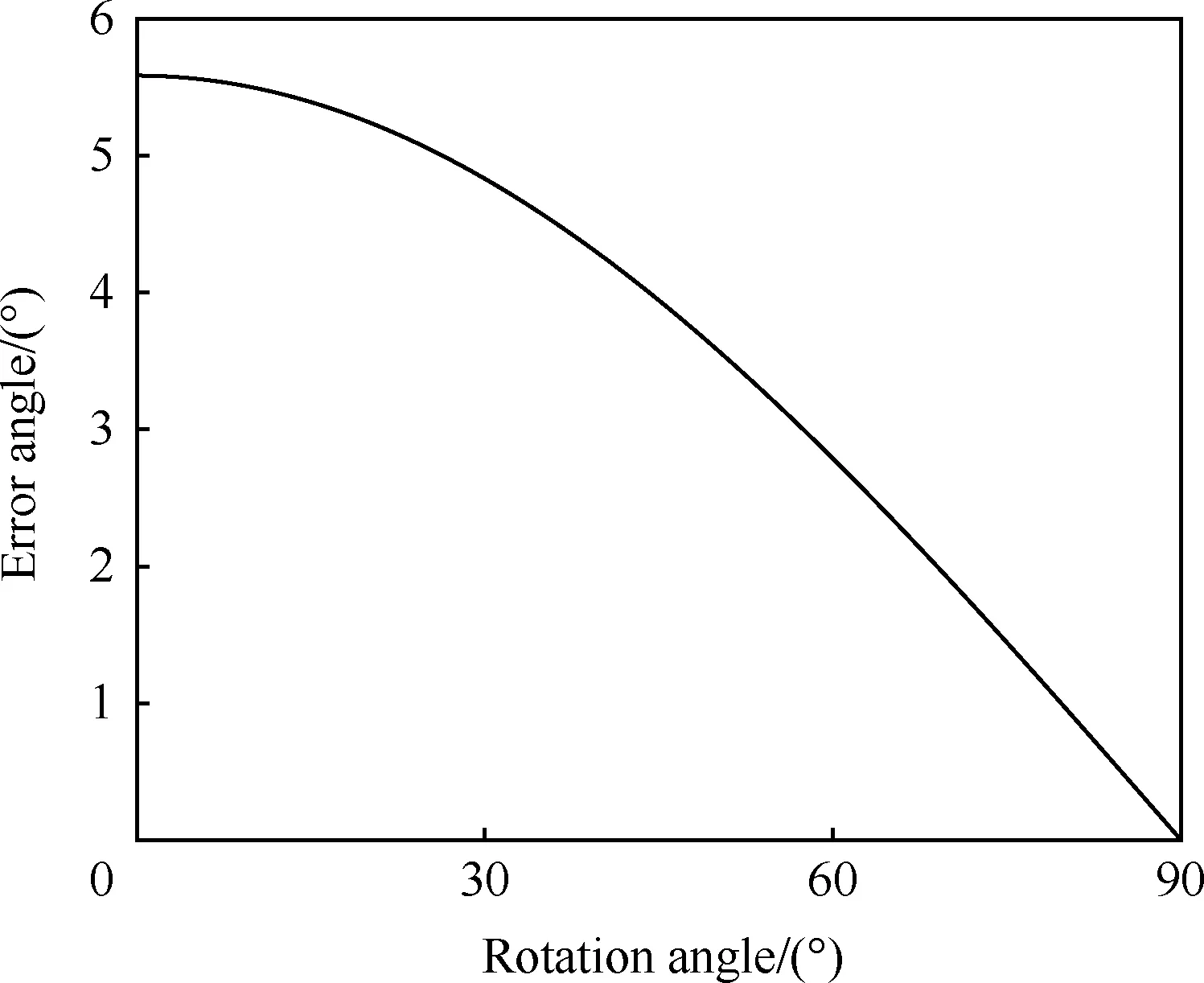
图4 误差角随干扰机旋转角的变化Fig.4 Variation of error angle with rotation angle of jammer

2.2.3 干扰机与雷达间距离对干扰效果影响

当干扰机两路信号幅值比为0.95、相位差为180°时，干扰机对雷达角度欺骗效果随两者距离变化的影响如图5所示。

从图5可知，随着雷达与干扰机距离的不断逼近，θs不断增大，交叉眼干扰的角度欺骗效果越好。如当雷达与干扰机距离r分别为1、4和6 km 时，θs的值分别为9.7°、2.8°和1.8°。

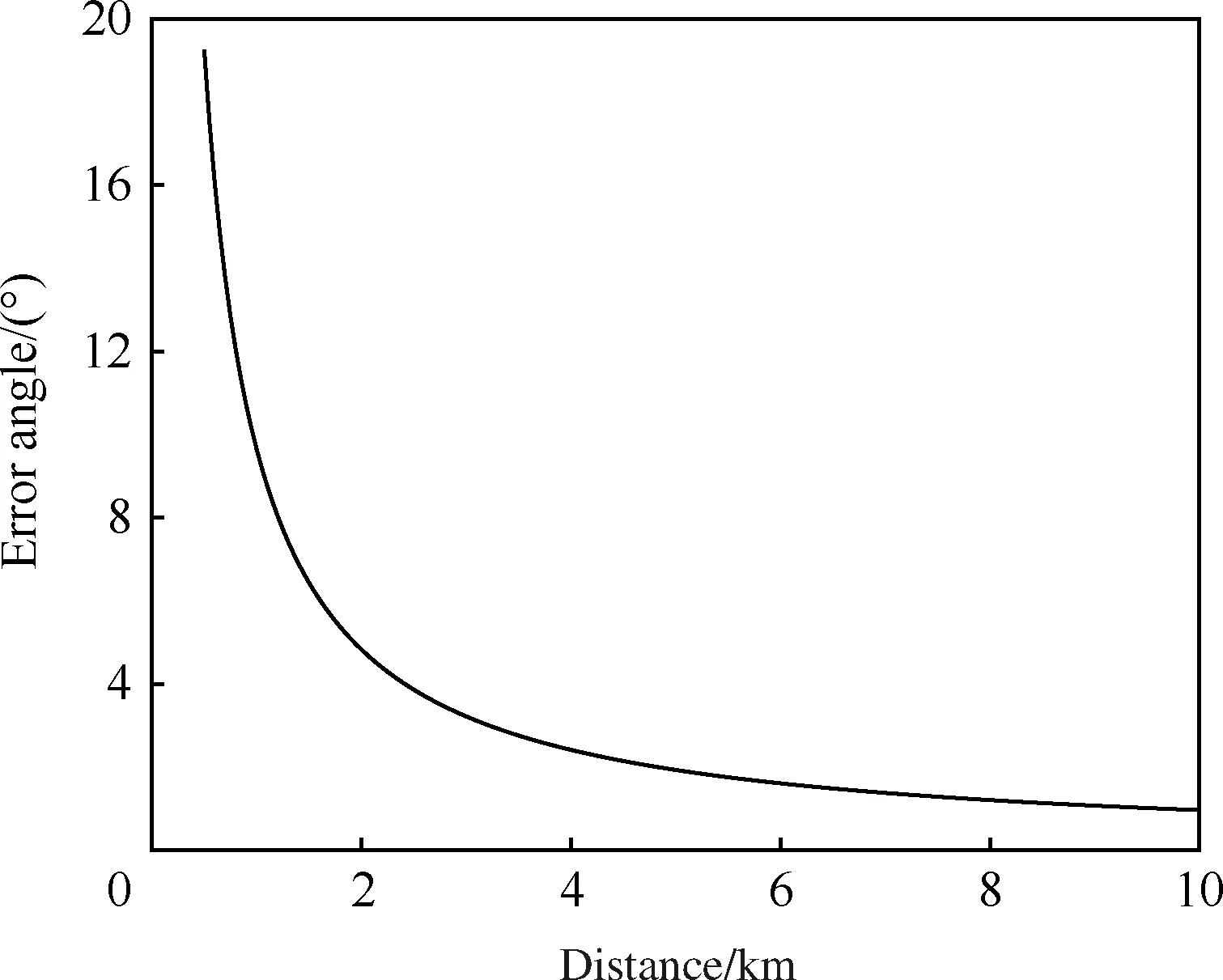
图5 误差角随干扰机与雷达之间距离的变化Fig.5 Variation of error angle with distance between jammer and radar

2.2.4 干扰机发射天线距离变化对干扰效果影响

当干扰机两路信号幅值比为0.95、相位差为180°时，干扰机对雷达角度欺骗效果随干扰机发射天线距离dc变化的影响如图6所示。

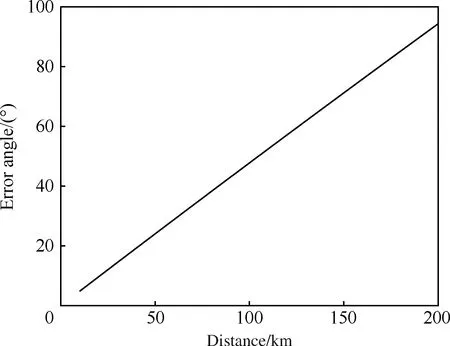
图6 误差角随dc变化Fig.6 Variation of error angle with dc

分析图6可知，当dc分别为20、100和200 m时，θs的值分别为9.9°、47.8°和92.9°，因此，在单脉冲雷达不可分辨干扰机单元的前提下，交叉眼干扰机的两发射天线间距越大，交叉眼干扰的欺骗效果越好。

2.3 交叉眼干扰模型仿真验证

2.3.1 不同幅值比和相位差

在3.1节仿真参数的基础上，当干扰信号幅值比分别为0.80、0.90和0.95时，数学模型计算得到单脉冲雷达指示角与仿真模型计算得到角度随信号相位差变化如图7所示。

从图7中可以得知，数学模型计算值与仿真模型计算值最大误差不超过0.2°，数学模型计算结果与仿真模型计算结果基本一致。

2.3.2 不同干扰机的旋转角

分析图8可知，在不同的θc值下，仿真模型与解析模型计算的结果一致，两者最大误差值不超过0.2°。

2.3.3 不同干扰机与雷达间距离

在2.1节仿真参数的基础上，取雷干扰机相对雷达视轴中心距离r分别为6、4、1 km时，仿真模型计算的角度与数学模型计算的角度随干扰机两路信号相位差变化曲线如图9所示。

分析图9可知，在不同距离下，数学模型输出结果与仿真模型输出结果一致。对比分析图9可知，这是因为随着距离的不断逼近，干扰机天线与雷达视轴中心的夹角θe不断增大，而交叉眼增益仅与交叉眼发射信号幅值比和相位差有关，因此交叉眼对单脉冲雷达的欺骗角会随距离的变小而增大。

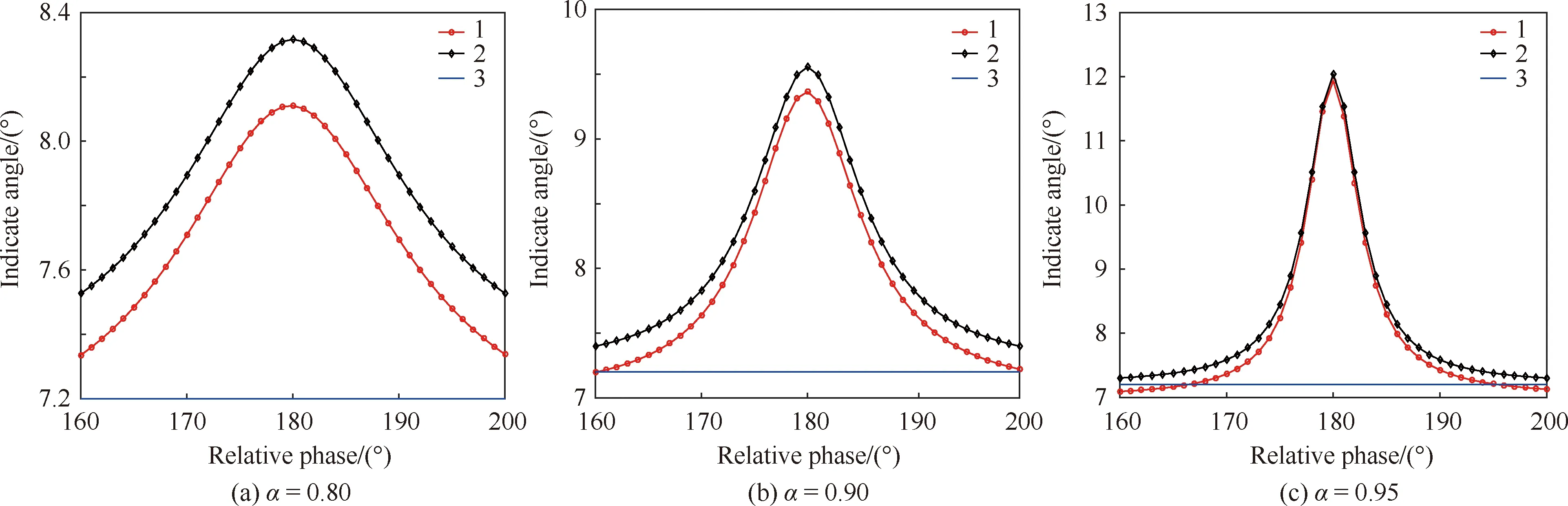
图7 解析结果与仿真结果对比Fig.7 Comparison of analytical results and simulation results

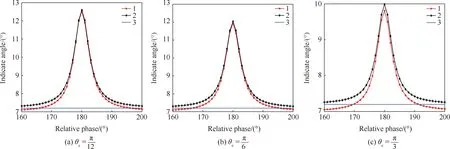
图8 不同转角下解析结果与仿真结果对比Fig.8 Comparison of analytical results and simulation results at different rotation angles

2.3.4 干扰机不同发射天线间距

在3.1节仿真参数的基础上,取r为2 km时，研究干扰机对雷达角度欺骗效果随干扰机两天发射天线间距的变化。当干扰机两发射天线间的距离dc分别为20、100、200 m时，仿真模型计算的角度与数学模型计算的角度随干扰机两路信号相位差变化分别如图10所示。

图10 不同dc下解析结果与仿真结果对比Fig.10 Comparison of analytical results and simulation results under different dc

对比分析图10可知，随着dc的增大，数学模型的误差越来越大，其原因亦是由于dc的增大而导致θe的增大，但正是由于θe的不断增大，导致数学推导模型在近似过程中与实际值的偏差亦在不断增加，如图10(c)中，在信号相位差为180°时，数学模型推导计算得到的单脉冲雷达指示角比仿真模型计算得到的单脉冲雷达指示角小150°左右，此时θe=2.4°，因此数学模型在dc过大时计算值与仿真值存在较大误差。

综上分析，引起数学模型与仿真模型差异的因素是θe，下面对θe大小变化引起仿真模型和数学模型的最大角度误差值进行分析，两者的最大误差值随θe变化如图11所示。

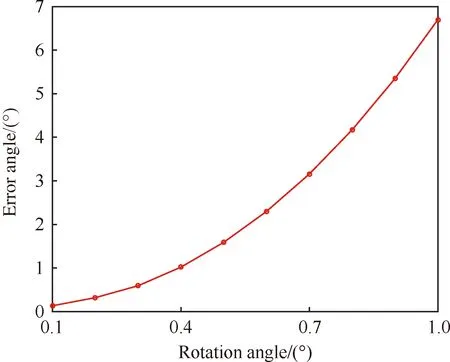
图11 角度误差值随θe的变化Fig.11 Variation of error angle with θe

分析图11可知，两模型输出的雷达指示角误差最大值随θe的增大呈指数化增大，目前已公开的弹载[24]单脉冲雷达波束宽度为5°，若以此为最大误差指标，则θe应小于0.9°。

2.4 参数敏感性分析

在交叉眼定型设计后，除影响交叉眼增益的幅值比、相位差等因素外，影响雷达指示角变化的因素有距离、干扰旋转角，现对雷达指示角随距离r、旋转角θc变化的敏感性开展分析。采取文献[25]中参数，分别采取文献[25]方法、式(14)以及单脉冲雷达仿真模型计算单脉冲雷达指示角，当θc=30°时，雷达指示角随距离变化如图12所示。当雷达与干扰机之间距离r=1 km时，雷达指示角随干扰机旋转角变化如图13所示。

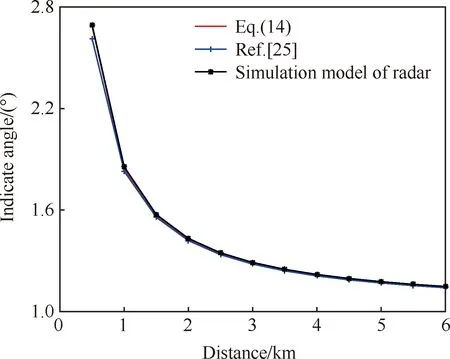
图12 雷达指示角随距离变化Fig.12 Variation of radar indicating angle with distance

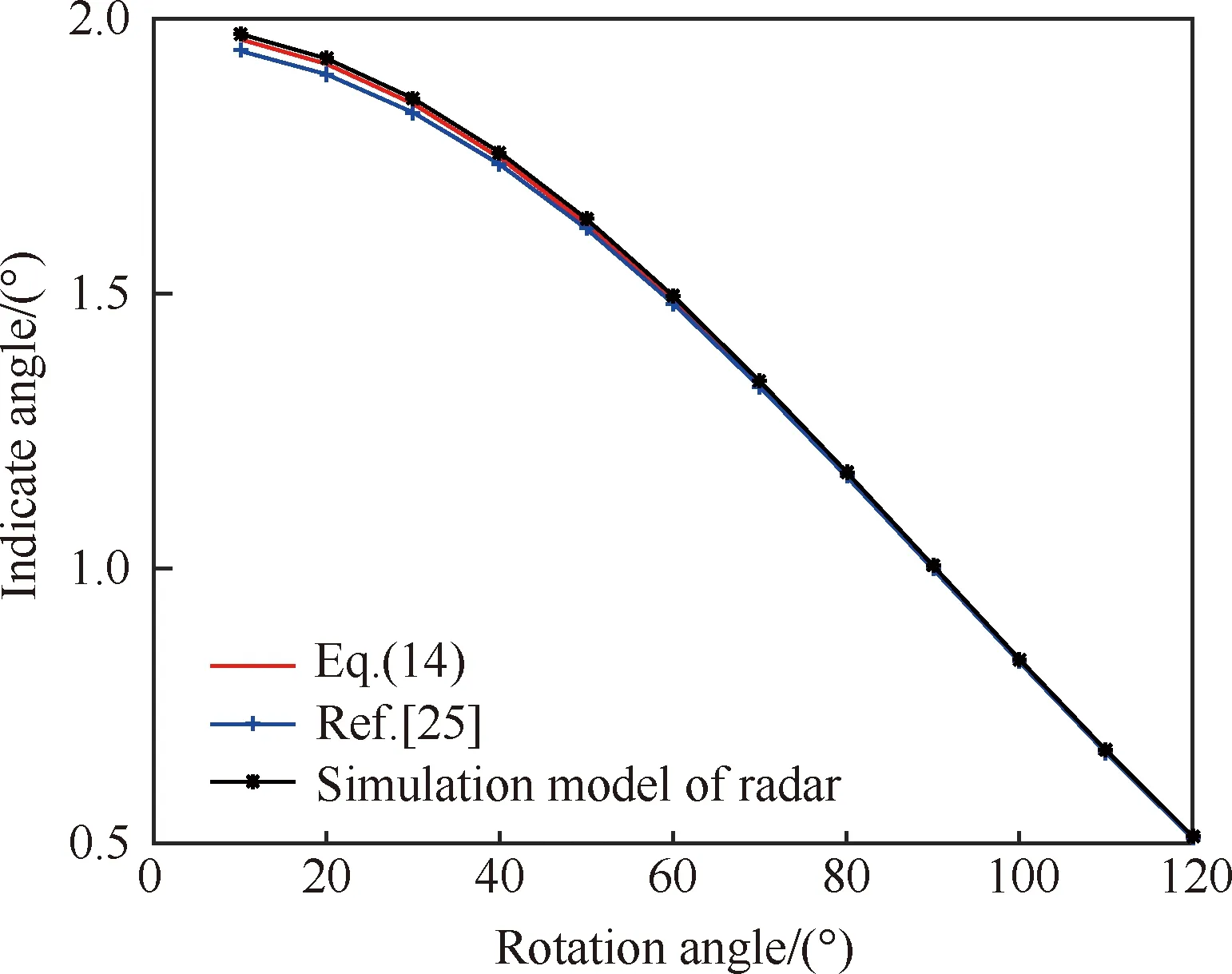
图13 雷达指示角随干扰机旋转角变化Fig.13 Variation of radar indicating angle with rotation angle

分析图12和图13可知，雷达指示角随雷达与干扰机距离的逼近，指示角呈指数增长，而雷达指示角随干扰机旋转角变化相对平稳。而搭载单脉冲雷达进行末制导的导弹会快速飞向目标，雷达指示角的快速变化会为干扰提供参考。另外，从图中可知，3种方法计算得到的雷达指示角较为一致，交叉眼对单脉冲雷达干扰效果分析可为交叉眼干扰设计提供一定的参考。

3 结 论

本文基于雷达方程、单脉冲雷达测角原理，在不考虑目标回波的条件下，建立隔离目标回波下的交叉眼干扰数学模型，并依据单脉冲雷达接收机角度信息处理流程，建立了单脉冲雷达接收机仿真模型。算例仿真分析结果表明：

1)当干扰信号均进入雷达接收机内时，单脉冲雷达越靠近干扰机发射天线中心轴、雷达与干扰机距离越近、干扰机发射天线间距越大，干扰机的角度欺骗效果越好。

2)雷达指示角随距离的逼近呈指数化增长，可为雷达识别交叉眼干扰提供参考。

3)数学模型和仿真模型计算的单脉冲雷达角度误差最大值随θe的增大呈指数化增长。

4)两点源交叉眼是交叉眼干扰的基本组成单元，其数学模型适用的局限性规律可为组阵的多点源交叉眼参考，本文研究可为交叉眼干扰工程设计提供一定的参考。