基于IDDES框架的γ -Reθ转捩模型

易淼荣，赵慧勇，乐嘉陵，肖保国，郑忠华

中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室，绵阳 621000

边界层转捩对高超声速飞行器的设计有利有弊。一方面，边界层转捩导致气动热的急剧增加，严重影响热防护系统的设计，同时转捩还影响飞行器的摩阻、压阻、飞行器的性能和气动力控制；另一方面，在高超声速进气道上实现边界层强制转捩，可以减少流动分离，提高流动抗逆压的能力，便于进气道的起动和超燃发动机的正常工作。在长达一个多世纪的研究后，人们对于边界层转捩问题的研究取得了长足的进步，发展了线性稳定性、弱非线性稳定性、瞬态增长、三波共振、二次失稳等理论[1]描述边界层转捩的过程，发展了静音风洞来模拟天上真实的来流扰动条件[2]。但是，针对一个给定的较复杂构型，人们仍不能确切地给出边界层会在什么条件下、什么位置由层流转捩为湍流，特别是在高超声速条件下，由于受到太多因素及各种因素之间互相耦合作用的影响，转捩预测变得更加困难。

目前能够进行边界层转捩研究的数值方法大致可分为4种：第1种是通过精细的空间和时间分辨率来解析边界层发展过程中扰动的物理发展过程，从而捕获边界层由层流转捩为湍流的详细信息，主要为DNS(Direct Numerical Simulation)和LES(Large Eddy Simulation)方法，被用来研究典型状态下的转捩机制和详细的转捩过程[3-4]，但是由于该方法对网格、格式和计算量的要求极大，很难针对高雷诺数、复杂构型开展研究。第2种是通过线性和非线性稳定性理论，通过对扰动增长率的研究从而获得边界层内扰动波的增长直至失稳过程，如LST(Linear Stability Theory)和PSE(Parabolized Stability Equation)方法[5-6]，其有明确的物理机制，能够模拟非稳定波线性(甚至是弱非线性阶段)的发展，但无法模拟Breakdown和湍斑生成的过程，也无法模拟Bypass转捩。第3种是通过对大量试验结果进行总结分析，提取出关键的流场参数，给定一个标准，当参数达到该标准时，则认为转捩发生，称之为转捩准则，如NASP(National AeroSpace Plane)的尖前缘平板转捩准则：Reθ/Mae=305[7]，其中Reθ为以动量厚度为长度尺度定义的雷诺数，Mae为边界层外缘马赫数。该方法形式简单，操作方便，但是通用性不好，只能针对类似的构型在类似的条件下开展转捩预测，而针对其他情况的预测就会出现偏差。

由于粗糙颗粒明显改变了边界层内流场的结构，其诱导的尾迹涡具有Görtler涡的性质，这种反向旋转的流向涡对导致边界层内的速度剖面出现大的变形，使得流向速度在法向和展向均存在拐点。Görtler涡结构在经历瞬态增长后，可能会与第2模态之间发生非线性耦合作用[21]或因其条带结构本身的不稳定性[22]而二次失稳并最终导致转捩的发生。如果采用足够精细的数值模拟方法，通过对涡的形成和破碎过程进行捕捉，理论上其可以捕获流向涡的形成、发展、失稳到转捩为湍流的整个过程。要捕获这些过程，目前可以采用的方法有DNS、LES和RANS/LES混合方法，而目前最有可能大范围工程应用的是RANS/LES混合方法。Yoon等[23]首先将DES方法应用于高超声速边界层内单个粗糙颗粒诱导转捩的算例，结果表明DES模型可以分辨大涡结构，可以用来模拟粗糙颗粒诱导的强制转捩；肖志祥等采用IDDES方法分别研究了高超声速下粗糙颗粒诱导平板强制转捩[24]和凹槽诱导转捩[25]的情况，给出了转捩涡结构的发展过程，表明采用IDDES方法对强制转捩开展研究是可行的，但其在进行模拟时，采用的是强制粗糙颗粒或者凹槽上游的流动为全层流的情况，因此在流过粗糙颗粒或凹槽之后，有一个从层流到湍流的转捩过程。IDDES方法之所以能够模拟强制转捩，是因为其能够解析更小尺度的涡，能够捕获粗糙颗粒或凹槽诱导出来的涡结构，但由于IDDES方法仍然是一个针对湍流的计算方法，当没有间歇因子来控制其湍动能方程时，针对没有明显大涡结构、由小扰动经过线性增长和非线性增长之后破碎再转捩为湍流的过程，其却无法捕获。而且纯粹的IDDES方法也无法反映来流湍流度对转捩的影响。根据普渡大学对于X-51A的试验结果[26]，来流湍流度对粗糙颗粒诱导的转捩仍然有重要的影响，因此来流湍流度也是一个不可忽略的因素。

针对γ-Reθ转捩模型和IDDES方法各自的优点和缺点，如果将γ-Reθ转捩模型与IDDES方法结合起来，则理论上可以克服各自的缺点，从而同时满足对自然转捩和强制转捩的模拟。实际上，早在2011年Sorensen等[27]就尝试过将γ-Reθ转捩模型与DES方法结合起来，并进行了大迎角机翼的计算，随后Alam等[28]则将DDES方法与k-kL-ω转捩模型[29]进行了结合，并将其应用在低压涡轮机叶片的转捩预测中。乔磊等[30]也尝试过将DDES方法与γ-Reθ转捩模型相结合，对低速平板算例进行了计算。以上结果均表明转捩模型与DES类方法结合后，能够像原始的γ-Reθ转捩模型一样对自然转捩进行模拟。但以上均为试探性研究，研究的构型都较为简单，都是低速领域的转捩，没有进一步发挥基于IDDES框架的转捩模型相对于传统转捩模型能够捕捉更精细的流场结构从而更精确地模拟强制转捩的这一优势。

本文希望通过结合γ-Reθ转捩模型对自然转捩模拟的优点和IDDES方法在模拟强制转捩时能分辨更精细物理结构从而捕获转捩过程的优点，将γ-Reθ转捩模型添加到IDDES方法的框架中去，从而实现对自然转捩和强制转捩更精确的模拟。在没有粗糙颗粒、凹槽等强制转捩因素时，网格只需满足RANS的网格要求即可，此时在边界层内RANS方法会被激活，并对转捩进行模拟。在有粗糙颗粒、凹槽等强制转捩因素时，采用更精细的网格，边界层内大部分区域LES方法被激活，可对涡结构的出现及发展过程进行捕捉，从而实现对强制转捩的模拟。

1 计算方法

本文搭建的基于IDDES框架的的γ-Reθ转捩模型是在课题组开发的大规模并行CFD平台AHL3D[31]上添加模块建立的，AHL3D 采用基于网格平均的有限体积方法离散求解Navier-Stokes方程组，定常时间推进采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法，非定常计算则包括显示的龙格-库塔法和隐式的双时间步法。无黏通量采用重构-推进方法，重构采用3阶MUSCL(Monotonic Upstream-centered Scheme for Conservation Laws)方法，本文在此基础上又添加了5阶WENO(Weighted Essentially Non-Oscillatory)重构方法。无黏通量的推进采用Steger-Warming通量分裂、AUSM+(improved Advection Upstream Splitting Method)、AUSMPW+(AUSM+ by Pressure-based Weighted function)和LDFSS(Low Diffusion Flux-Splitting Scheme)4种计算格式。黏性通量采用改进的Gauss定理计算。湍流模型中包含了本文需要用到的剪切应力输运(SST)双方程模型。作者团队在文献[20]中已经实现了γ-Reθ转捩模型的搭建和应用，因此本文以该转捩模型为基础，先实现IDDES方法，然后将IDDES方法与γ-Reθ转捩模型相结合，重新对转捩模型进行标定，从而实现本文计算方法的建立。

1.1 γ-Reθ转捩模型

γ-Reθ模型详细的计算公式可参考文献[9]。其通过间歇因子γ对SST模型湍动能k方程的产生项和破坏项进行控制，进而控制整个转捩过程。间歇因子输运方程为

(1)

式中：ρ为密度；Uj为xj方向的雷诺平均速度；μ为分子黏性系数；μt为湍流黏性系数；σf=1.0为常数；Pγ和Eγ分别为γ方程的产生项和破坏项，Pγ的形式为

Pγ=Flengthca1ρS(γFonset)0.5(1-ce1γ)

(2)

其中：Fonset为决定转捩开始的阈函数；Flength为转捩区域长度；其余相关参数的含义详见文献[9]。

(3)

式中：Reν为当地涡雷诺数；Reθc为临界动量厚度雷诺数。

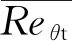
(4)

(5)

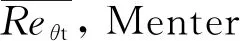
(6)

(7)

Reθt=f3(Tu)f4(λθ)

(8)

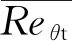
此外，γ-Reθ模型还考虑了分离诱导转捩的作用。

(9)

γeff=max(γ,γsep)

(10)

式中：γsep为分离区的间歇因子；γeff为最终的间歇因子；Freattach为与再附区有关的参数，具体形式参见文献[9]。其可通过改变经验参数s1来调节对分离诱导转捩的敏感度。最后，转捩模型对SST模型k方程的作用方式为

(11)

式中：Pk和Dk分别为SST模型中k方程的产生项和破坏项。

1.2 γ-Reθ转捩模型与IDDES方法的结合

γ-Reθ模型通过添加两个输运方程求解间歇因子γ，且通过γ作用于k方程的产生项和破坏项从而与SST湍流模型结合。在形式上，添加基于SST模型的IDDES方法则更为简单，可以通过修改湍动能输运方程破坏项中的长度尺度函数而实现[32]。SST模型中湍动能方程为

(12)

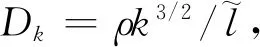
(13)

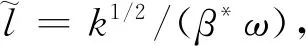
长度尺度函数从DES到IDDES发展历程的具体情况可参见文献[33]，本文仅给出lIDDES的计算形式。lIDDES与网格尺度Δ有关。

Δ=min{max[Cwdw,Cwhmax,hmin],hmax}

(14)

式中：hmax=max(Δx,Δy,Δz)，hmin=min(Δx,Δy,Δz),Δx、Δy、Δz分别为x、y、z这3个方向上的网格尺度；dw为距壁面距离；Cw为与亚格子模型无关的经验常数，一般取Cw=0.15。

lIDDES的形式为

(15)

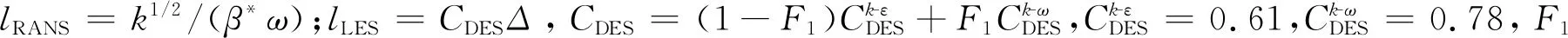
(16)

fdt=1-tanh[(Cdtrdt)3]

(17)

(18)

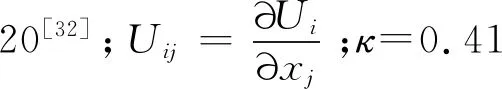
fB=min{2exp(-9α2),1.0}

(19)

其中:α=0.25-dw/hmax。至此，lIDDES求出。

将RANS框架换成IDDES框架后，会对转捩模型产生2个方面的影响：

2 IDDES方法的验证

超声速混合层流动是典型的以大尺度涡结构为主导的可压缩自由剪切层湍流流动。本节通过Goebel的混合层试验[34]来检验本文的IDDES方法对大尺度涡结构的捕捉能力以及对平均量和脉动量的预测能力。

Goebel的试验构型[34]如图1所示，混合区总高48 mm，总长500 mm，隔板下部倾角为2.5 °，尖劈厚度为0.5 mm。混合区入口参数如表1所示。计算中为满足混合区入口处的附面层厚度，参考文献[33]中的做法，将隔板上部入口选在混合区入口前67 mm处，隔板下部入口选在混合区入口前42 mm处。

计算求解二维非定常Navier-Stokes方程组，采用基于SST模型的IDDES方法进行模拟。无黏通量重构采用五阶WENO方法，分裂采用AUSMPW+格式，黏性通量采用改进的高斯定理，时间推进采用隐式双时间步法，物理时间步长为5×10-8s，子迭代最大步数为15，子迭代CFL数为0.8。上下壁面采用对称边界条件，隔板采用绝热壁条件，出口采用外推。混合区网格量为1 001×261，垂直壁面第1层网格法向长度取0.01 mm。隔板上下的初始条件分别设为上下入口的来流。计算经过1 ms后流场充分发展并稳定，再计算1 ms,统计1～2 ms时的平均量。

计算得到的t=1 ms时的流场结构如图2所示。从图中可以看出，本文IDDES方法能够分辨混合层中大尺度涡结构的形成、发展和脱落过程。t=1～2 ms期间的3个不同流向位置的时间统计平均流向速度U无量纲化之后的分布如图3所示，图中h=48 mm为混合区总高度，U2=399 m/s为混合层下层入口速度，ΔU=301 m/s为上下层入口速度之差。x=50 mm时，计算得到的混合层比试验稍薄，这可能是由于来流条件中没有给定脉动值，造成剪切层发展比试验值要稍慢导致的。而到x=100 mm和150 mm时，计算与试验吻合得非常好，此时旋涡开始变大并脱落，混合层厚度明显增加。

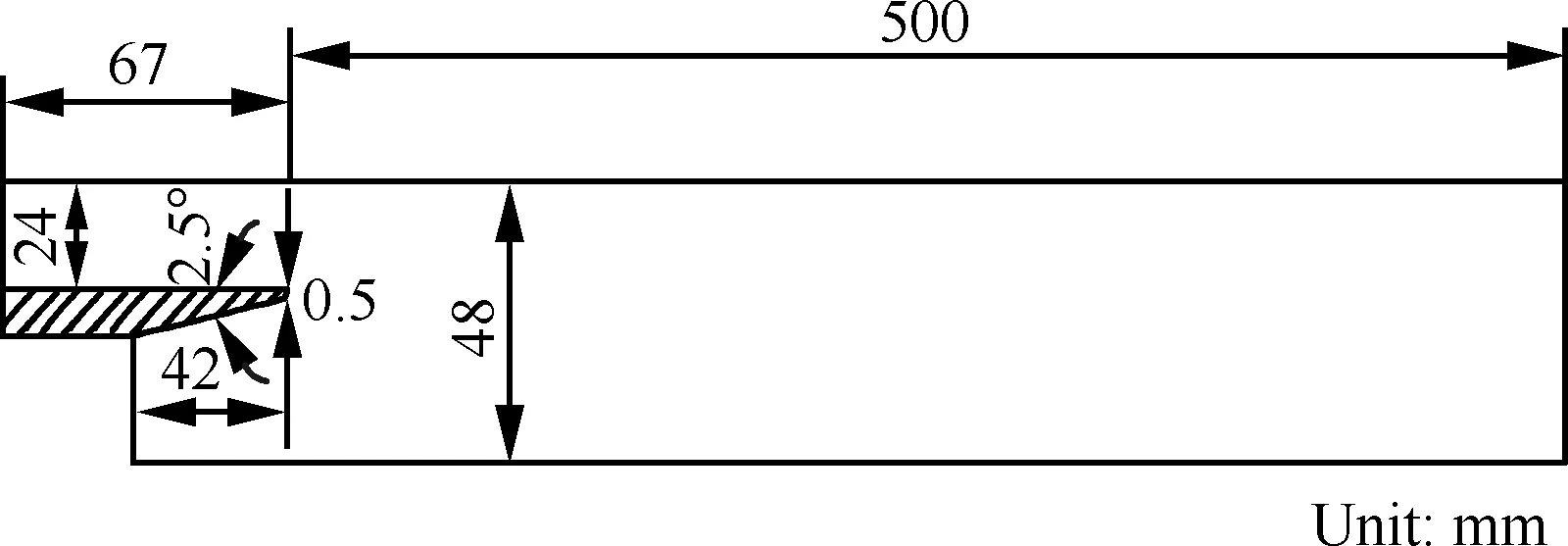
图1 Goebel的混合层试验示意图[34]Fig.1 Sketch of Goebel’s mixing layer test[34]

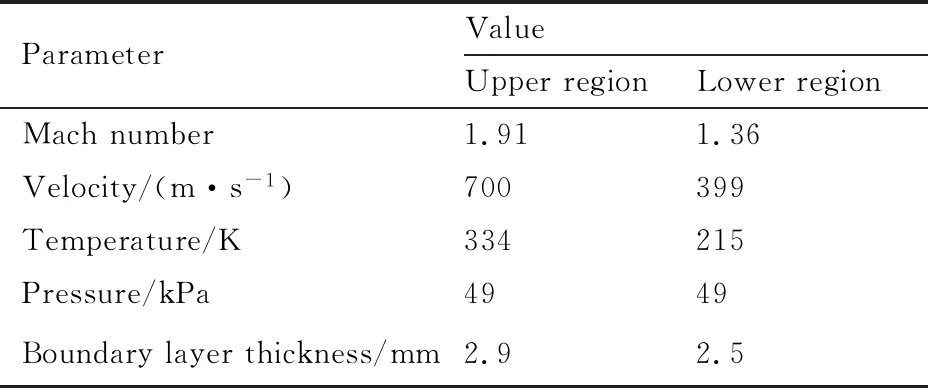
表1 混合区入口来流条件Table 1 Free stream conditions of mixing region inlet

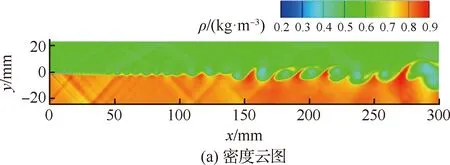
图2 二维超声速混合层流场结构Fig.2 Flow field structures of two-dimensional supersonic mixing layer

图4和图5则分别为流向脉动速度均方根urms和法向脉动速度均方根vrms的分布，流向脉动速度均方根在x=50 mm时仍然比试验值偏小，这与平均速度显示混合层偏薄相一致。而在x=100 mm 和150 mm位置的流向速度均方根则与试验吻合良好，表明本文计算方法能够有效捕捉到流场大涡结构。而法向速度均方根则在x=50 mm时与试验吻合较好，在x=100 mm和150 mm时较试验值要明显偏大，计算得到的流向、法向速度脉动在同一位置基本是同等量级的，但试验测量到的流向脉动要大于法向脉动，计算与试验的差别可能是由于计算是采用二维模拟而导致的。总体来说，计算结果与试验结果的对比表明本文计算方法足以分辨超声速混合层中的大涡结构，可应用于可压缩湍流的模拟。

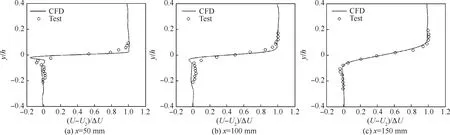
图3 不同流向位置的时间统计平均流向速度分布Fig.3 Distribution of time-average streamwise velocity in different streamwise positions

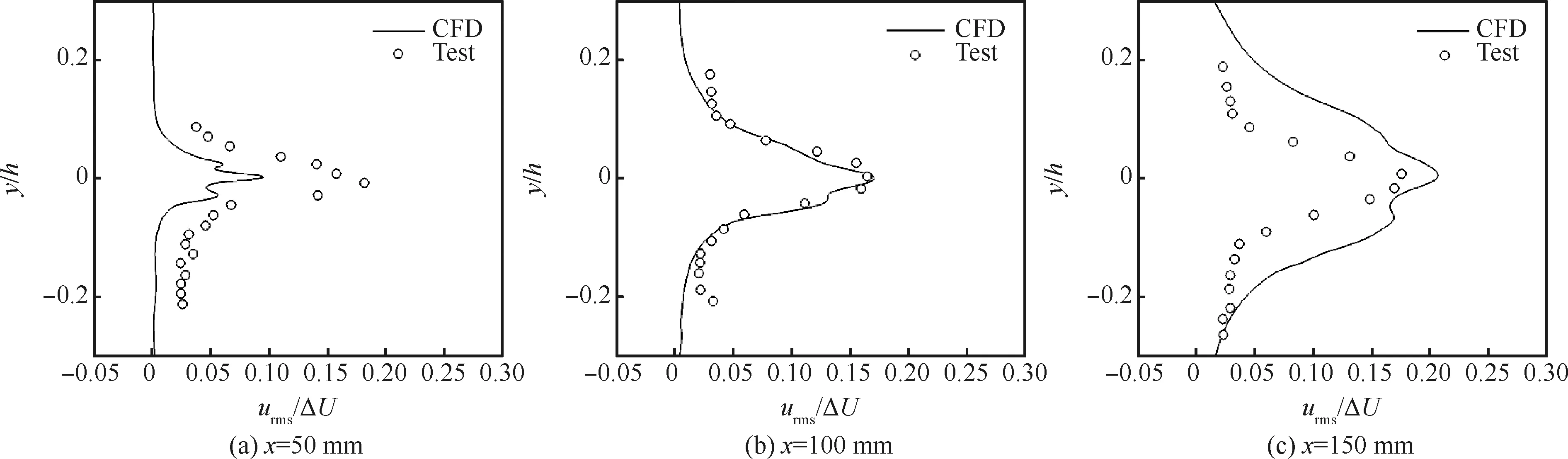
图4 流向脉动速度均方根分布Fig.4 Root-mean-square distribution of streamwise velocity fluctuations

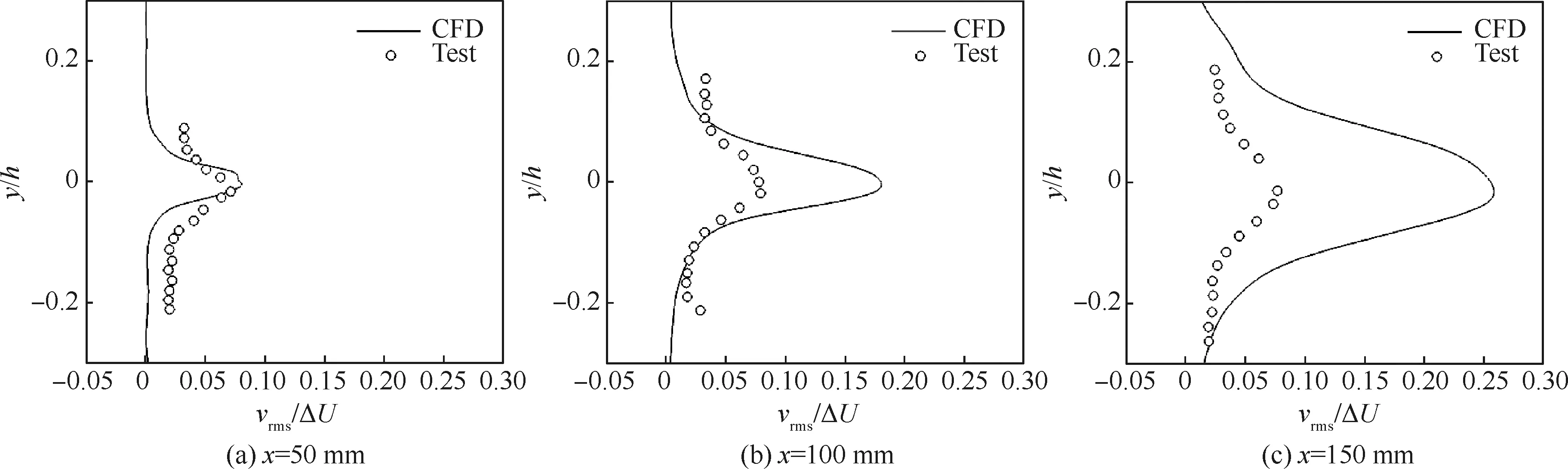
图5 法向脉动速度均方根分布Fig.5 Root-mean-square distribution of vertical velocity fluctuations

3 基于IDDES方法的γ-Reθ转捩模型的建立及验证

γ-Reθ转捩模型可以反映雷诺数对转捩的影响，也可以通过式(8)反映压力梯度、湍流度对转捩的影响，但由于其对转捩位置的预测受到计算方法、格式等多方面因素的影响，因此每一个框架上搭建的γ-Reθ转捩模型都可能需要进行重新标定。作者团队基于在文献[19-20]中采用γ-Reθ模型进行计算的经验，得到以下几点结论：

1)在AHL3D框架上搭建的基于RANS的γ-Reθ转捩模型如果直接采用原始的经验关系式进行高超声速转捩模拟，得到的转捩位置整体会比实际转捩位置大大提前。

2)通过重新标定将转捩位置整体推迟后，添加Forsythe[35]的可压缩性修正可有效反映可压缩性对转捩的影响，使得该方法能在较宽马赫数范围内对转捩进行模拟。

基于以上经验，本文拟对基于IDDES方法的γ-Reθ转捩模型进行如下修改：

1)加入Forsythe的可压缩性修正。

2)经验耦合关系式仍然采用Langtry的原始关系式，参考文献[15]中的做法，将式(3)中的2.193调整为3.5。

3)式(9)中，常数2会致使γ在分离区直接变为2，导致k值的增加，从而致使本应由LES方法处理的区域被程序自动判断为RANS处理区域，这样会导致分离区的精细流动因采用RANS方法而被抹去，实际上，当将RANS方法改为IDDES方法后，对分离流的捕捉要更加精细，因此，为了适当弱化模型对分离诱导转捩模化的功能，当需要用IDDES方法来分辨流场内的精细流动时，将式(9)中的常数2改为1。

3.1 马赫数为3.5的尖锥转捩

Chen和Malik[36]在NASA兰利研究中心的马赫数Ma=3.5低扰动风洞中进行了半锥角为5°的尖锥转捩测量，其来流单位雷诺数Re由2.81 ×107/m变化到7.8×107/m，得到了相同马赫数条件下雷诺数对转捩位置的定量影响规律。采用该算例不仅可以验证模型对可压缩流转捩的模拟能力，也可以验证模型是否能正确反应雷诺数对转捩的影响规律。

本文选取了其试验中的6个不同来流雷诺数进行计算，并与试验得到的转捩位置进行对比。计算设置的来流条件如表2所示，表中T0和P0分别为来流总温和总压。尖锥迎角为0°，壁面温度统一设为绝热壁，来流湍流度设为0.4%，来流黏性比RT=1.0。计算采用轴对称模型进行，方法为基于IDDES框架的γ-Reθ转捩模型，无黏通量采用WENO五阶重构和AUSMPW+格式。模型全长为381 mm。尖锥流向和法向的网格量为341×201，壁面第1层网格距离壁面0.001 mm。

由于试验是通过测量温度恢复系数来判断流动是层流还是湍流，而真实的温度壁面条件在计算中并不好给定，因此本文采用摩阻系数来判断转捩位置，且只与试验对比转捩位置，计算结果如图6所示，其中Cf为摩阻系数，r为温度恢复系数。从图中可知，随着来流雷诺数的增加，转捩位置由约0.28 m逐渐前移至0.1 m左右。模型可以反映可压缩条件下雷诺数变化对转捩的影响。

表2 马赫数为3.5的尖锥转捩来流条件Table 2 Free stream condition of sharp cone transition tests with Mach number of 3.5

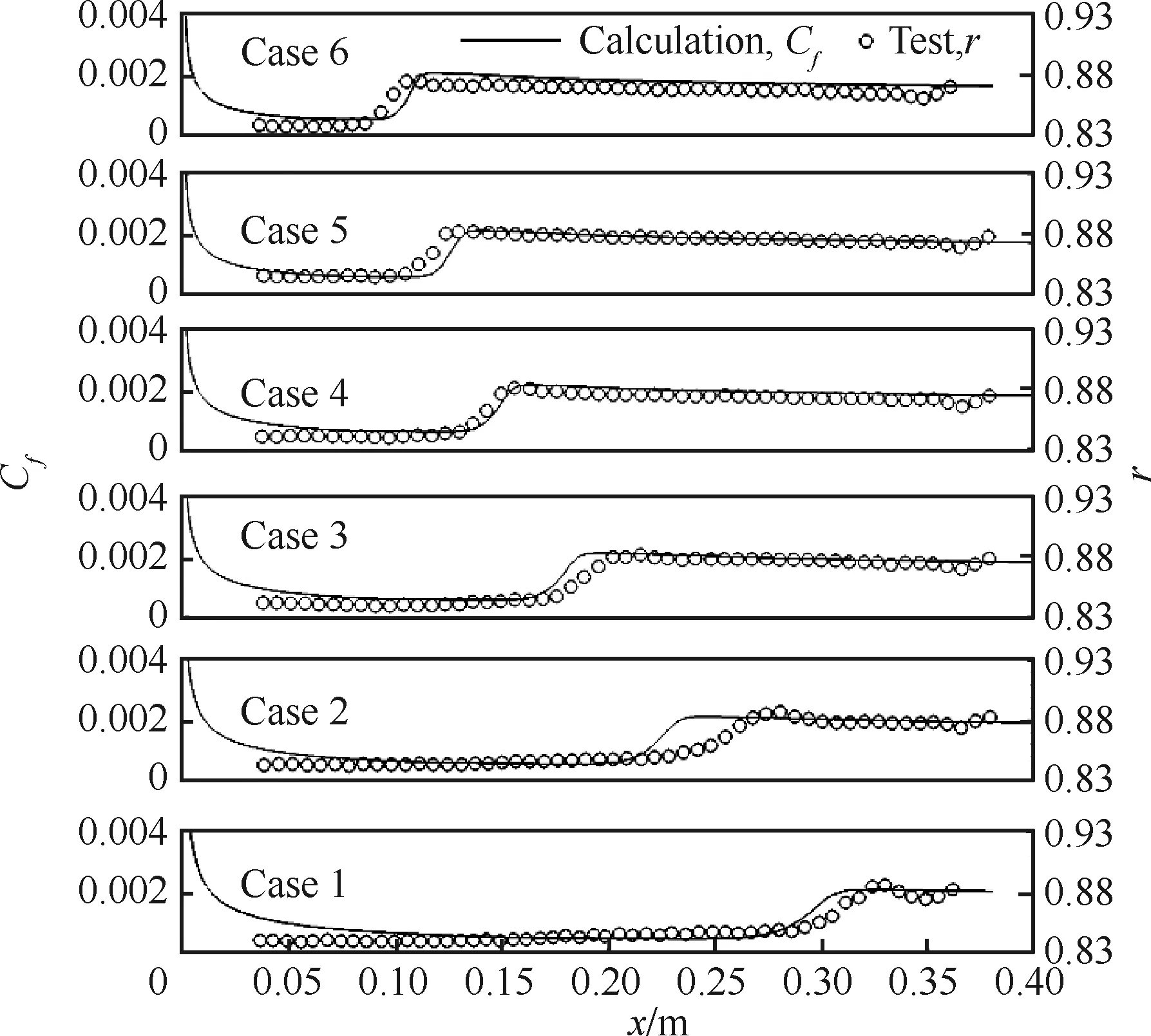
图6 不同Re下的尖锥转捩Fig.6 Transition of sharp cone with different Re

3.2 马赫数为8.1的双锲转捩

Neuenhahn和Olivier[37]在德国TH2高超声速激波风洞中进行了来流马赫数为8.1的双锲中边界层与激波干扰的试验。试验研究了壁温和熵层对激波边界层干扰的影响。在研究者后续针对该问题的CFD研究中发现，该试验中包含了边界层转捩现象，因为单纯的层流或湍流均无法正确得到压力分布和分离区大小。其中Krause[16]和Zhang[17]等均采用该算例对可压缩条件下的γ-Reθ转捩模型进行了验证。本文采用二维计算，模拟了尖前缘、前缘半经R为0.5 mm和1.0 mm这3个不同模型在同一来流条件下的试验情况。构型如图7所示，第1楔长度L1=180 mm，倾斜角为9°，第2楔长度L2=255 mm，拐角为11.5°。来流马赫数为8.1，总压为5.7 MPa，总温为1 430 K，单位雷诺数为3.8×106/m。壁温设为300 K，来流湍流度设为0.5%，来流黏性比RT设为1。计算方法同3.1节，网格总量约为3.4万，第1、2楔面的流向网格数分别为121和101，法向网格数为131，壁面第1层网格距离壁面小于0.002 mm。

计算得到的壁面压力(p)分布如图8所示，从图中可知，层流与湍流计算出来的拐角位置的分离泡大小有很大区别，而试验值均介于层流和湍流计算结果之间，确实存在明显的边界层转捩现象。同时，分离泡的大小随R由0 mm增加到1.0 mm而逐渐增大，表明转捩位置随着前缘钝度的增大而逐渐后移。计算结果反应出了边界层转捩给分离泡大小带来的影响，也反应出了前缘钝度(0～1.0 mm范围内)对转捩的影响规律。

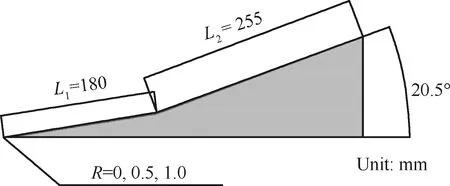
图7 双楔试验构型示意图[37]Fig.7 Sketch of double wedge geometry[37]

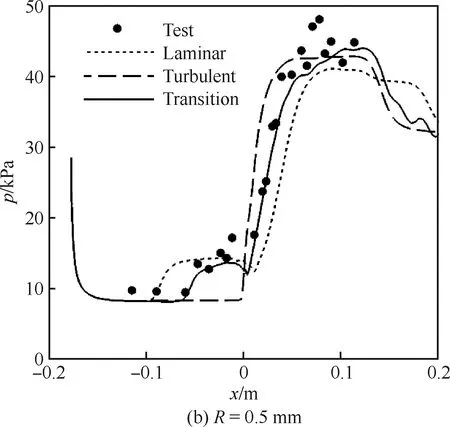
图8 不同前缘半径下双楔的壁面压力分布Fig.8 Wall pressure distribution of double wedge with different leading edge radiuses

3.3 平板上单个粗糙颗粒诱导的转捩

对基于IDDES方法的γ-Reθ转捩模型进行修改并经过自然转捩算例验证后，对单个粗糙颗粒诱导高超声速边界层转捩的情况进行模拟，分析转捩过程。本文选取了Tirtey等在高超声速VKI H3风洞中进行的强制转捩试验[38-39]进行模拟。Tirtey等研究了圆柱形、钻石型、斜坡型的单个粗糙颗粒诱导转捩的情况，本文选取其圆柱形粗糙颗粒在高雷诺数下的情况进行模拟。模型如图9所示[38]，一块长 290 mm、宽100 mm、前缘钝度为0.5 mm的平板，在距前缘60 mm处安装了一个粗糙颗粒，其参数为：a=4 mm，b=1.02 mm。本文只模拟了其长170 mm、宽40 mm的区域，流场区域高20 mm，如图10所示。来流马赫数为6，来流单位雷诺数为2.7×107/m，来流总压为3.1 MPa，总温为500 K，壁温在试验开始时均为292±2 K，试验结束后层流区最大温升为4 K，湍流区最大温升为12 K，由于这里壁温变化都不大，因此选取300 K为壁面温度。整个流场的网格量约为3 500万，平板第1层网格距离壁面0.002 mm，对应的y+小于0.1。粗糙颗粒下游的流场流向、法向、展向的网格分别为601×151×207，对粗糙颗粒周围的流场进行了加密。粗糙颗粒后缘的流向和展向网格间距分别为0.005 mm和0.03 mm，对应无量纲网格尺度Δx+<0.1，Δz+<1，尾迹区的网格间距随着流向距离的增大而逐渐增加，到x=170 mm位置时，Δx=0.6 mm，Δz=0.2 mm，对应的Δx+≈18，Δz+≈6。

计算得到的以Q等值面表示的流场涡结构如图11所示(图中T为温度)，可以看出粗糙颗粒诱导出的马蹄涡和剪切层除了向下游发展外，还有明显的往展向拓宽趋势，这符合湍流的性质，也与试验结果相符。图12给出了壁面Stanton数(St)分布。可知，采用基于RANS的γ-Reθ转捩模型得到的粗糙颗粒尾迹在x=70 mm(粗糙颗粒后缘下游10 mm处)位置时宽度约为12 mm，在x=170 mm位置的宽度约为14 mm，试验测量得到的尾迹宽度在x=70 mm时约为9 mm，在x=170 mm时约为22 mm，而采用基于IDDES方法的γ-Reθ转捩模型得到的尾迹宽度在x=70 mm时约为9 mm，在x=170 mm时约为20 mm。显然本文模拟结果与试验情况更为接近。

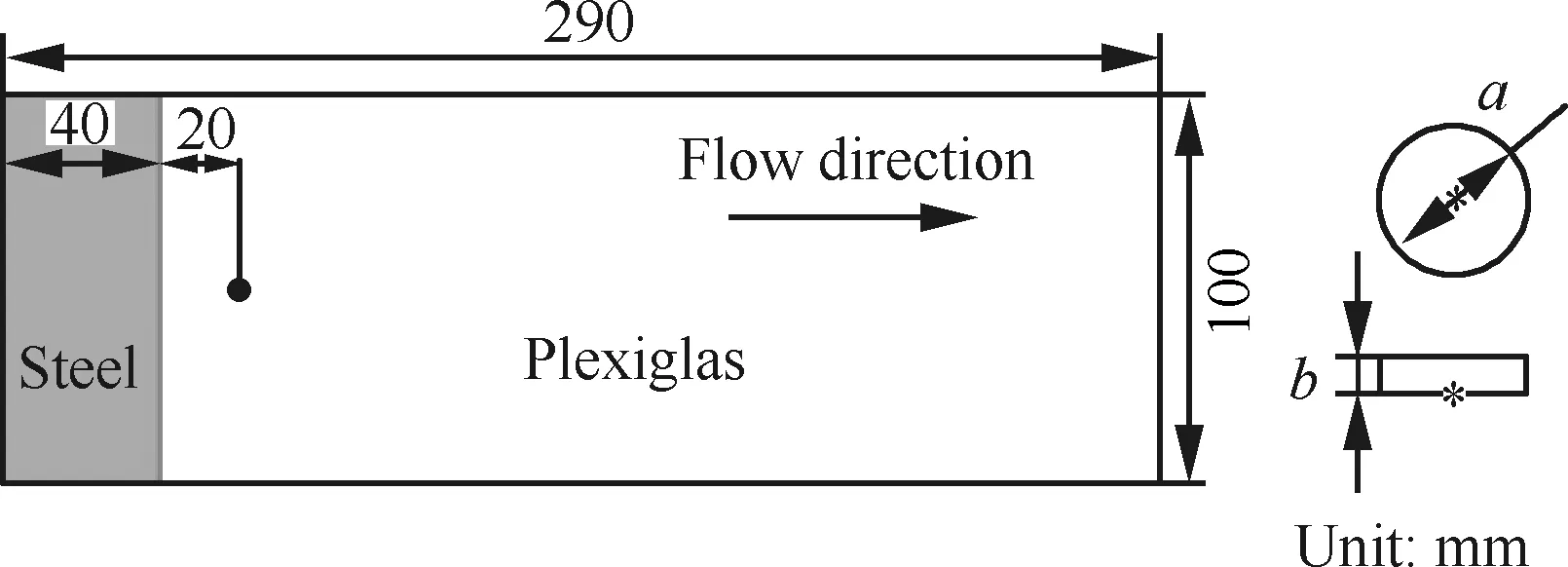
图9 平板模型示意图[38]Fig.9 Sketch of panel model geometry[38]

图10 流场及网格拓扑示意图Fig.10 Sketch of topology of flow field and grid

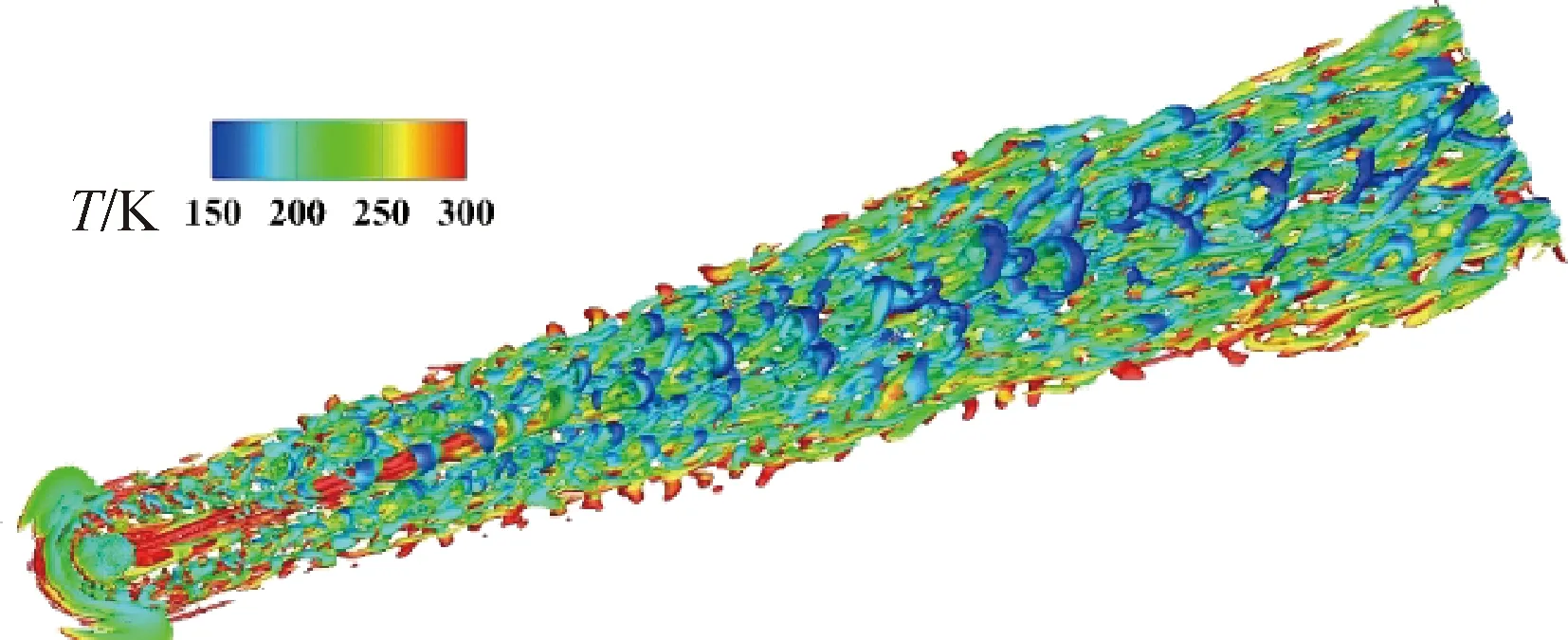
图11 以温度染色的Q等值面图Fig.11 Iso-surfaces of Q colored by temperature

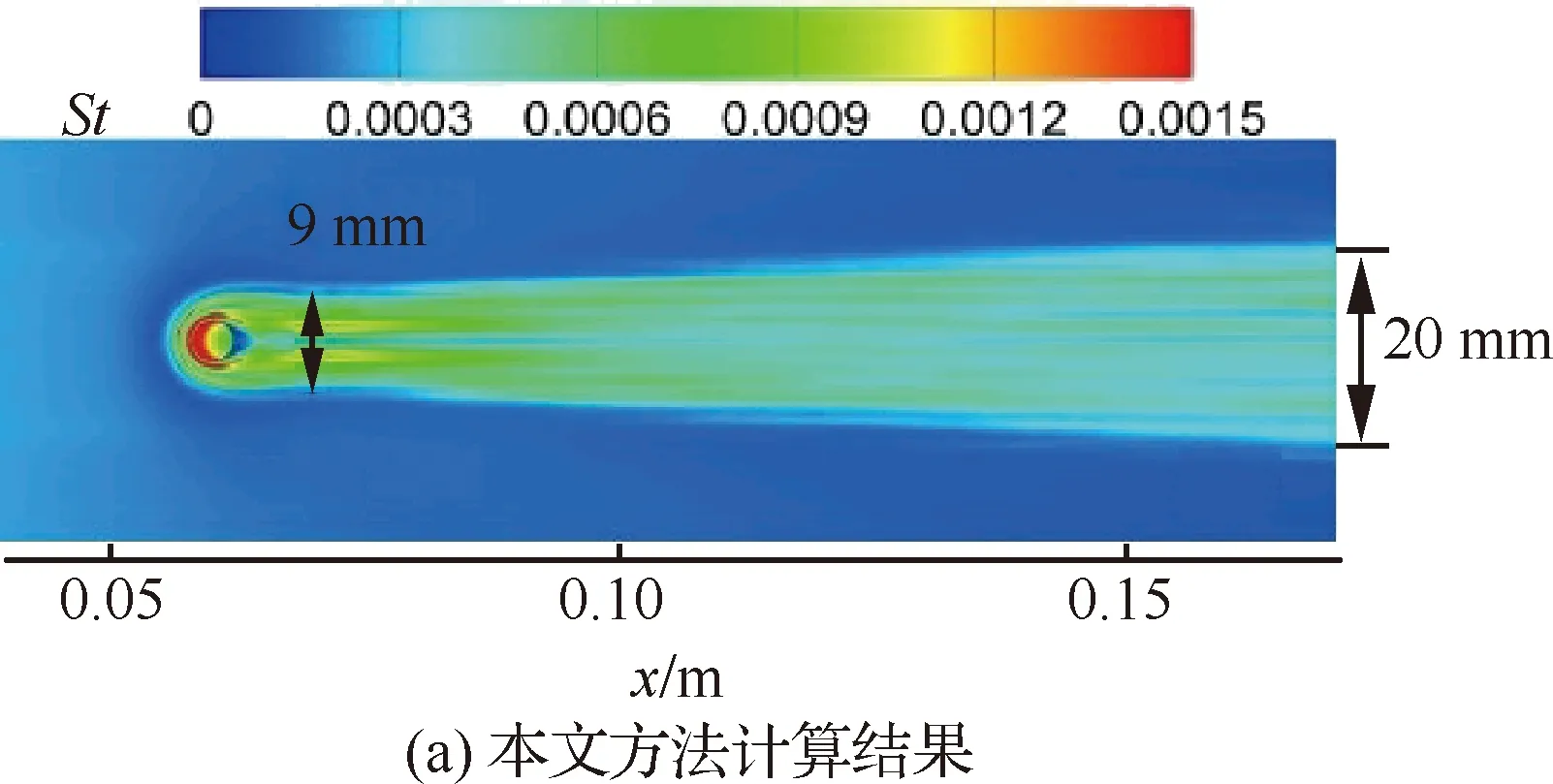
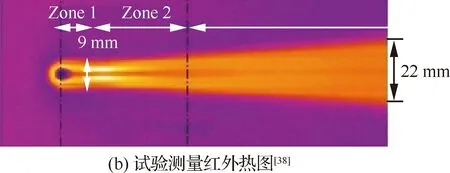
图12 壁面St分布Fig.12 St distribution on wall

图13为本文计算得到的St在尾迹区(对称面上)及非尾迹区的分布与试验对比，可知，计算与试验基本吻合，St在粗糙颗粒后缘均先剧烈增大(由粗糙颗粒后缘诱导出的尾迹涡导致)并迅速衰减，再经历一个相对缓慢的增长过程，达到极大值后开始随着流向距离的增加逐渐减小。若定义St达到全湍流值之前的极大值点为转捩结束位置，则计算得到的转捩结束位置为x≈120 mm，对应的转捩雷诺数约为3.24×106，而试验得到的转捩结束位置为x≈108 mm，对应的转捩雷诺数约为2.92×106。二者在转捩位置和尾迹展向发展的差别的原因可能是本文的计算方法虽然一方面捕捉到了粗糙颗粒尾涡的形成、发展及失稳过程，另一方面也模化了自然转捩时扰动发展导致转捩的过程，由于来流扰动是以湍动能k值的形式给定的，而非直接给定具体形式的脉动，因此无法反映来流扰动与粗糙颗粒之间的耦合作用，而在该试验中，风洞为常规噪声风洞，因此边界层内粗糙颗粒之前的扰动可能已经足够大并与粗糙颗粒产生了耦合作用，而目前本文的方法并不能反映出这种耦合作用。

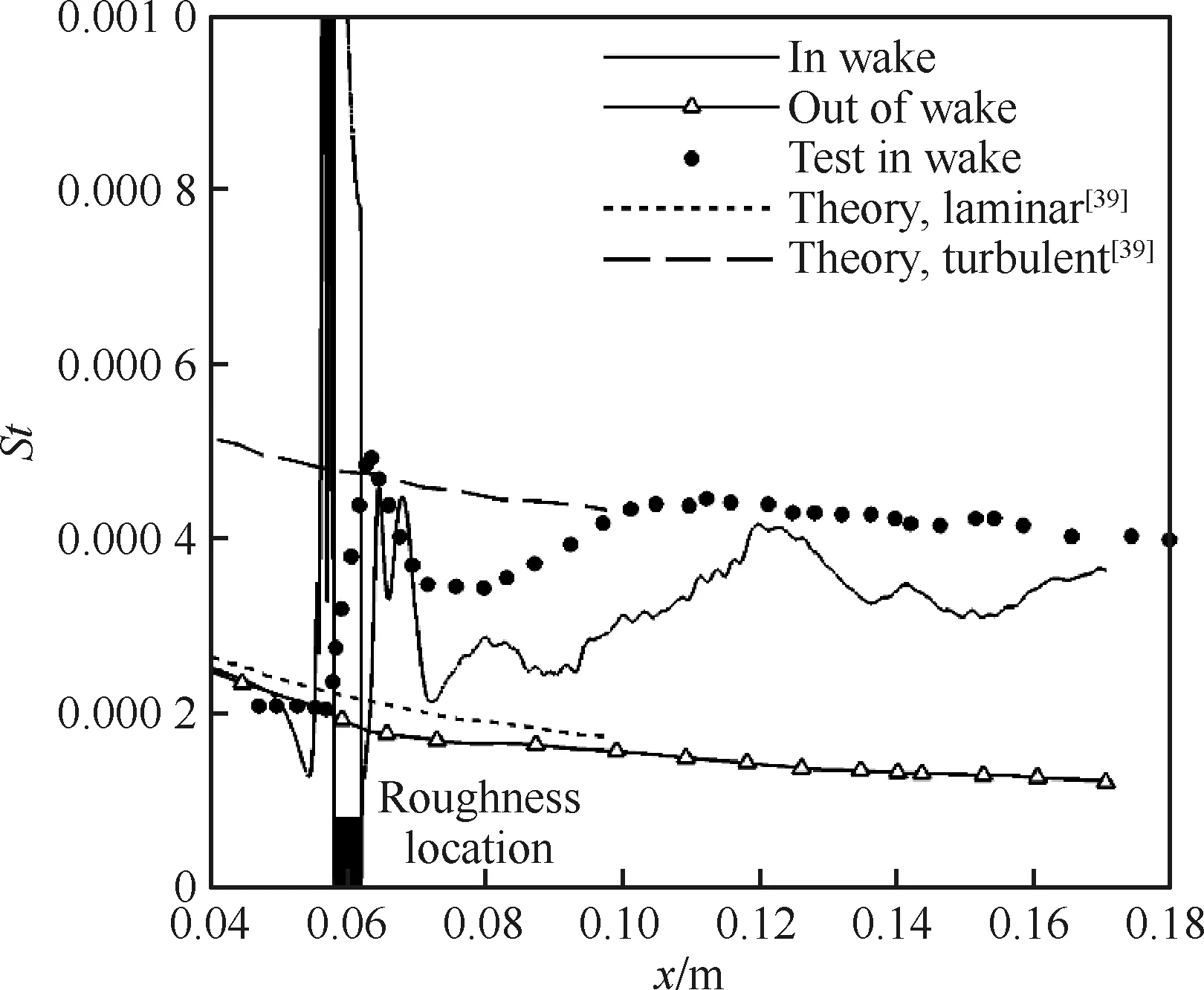
图13 尾迹区与非尾迹区的St分布Fig.13 St distribution of wake region and out of wake region.

图14为计算得到的粗糙颗粒附近对称面流线和壁面摩擦力线图与Tirtey给出的流场结构对比。从图中可以看出，粗糙颗粒前缘诱导出了微弱的斜激波，而在颗粒前缘上游则存在较大的分离区，较大的分离涡又诱导出二次反向分离涡，致使粗糙颗粒周围的摩擦力线存在3条分离线和3条再附着线，分离涡向下游发展，形成了马蹄涡结构，数值模拟对粗糙颗粒附近的流场结构的模拟与试验基本一致。

图15给出了对称面上的流场结构，分别为x方向的密度梯度、流向涡大小及速度脉动的均方根分布，其中u∞表示来流速度。从图中可知，在对称面上，粗糙颗粒上部除诱导出了斜激波外，还诱导出了较强的剪切层，该剪切层厚度很薄，扰动量级很大，但基本维持在边界层外缘，实际上，在粗糙颗粒下游，距离壁面较近的底层也出现了剪切层，底层部分的剪切层在向下游发展的同时也在向上层发展，同时厚度逐渐增厚，涡结构最终破碎，扰动扩散至整个边界层，扰动在x=120 mm位置附近达到一个极大值之后，扰动幅值不再继续增加，此时转捩已经完成。

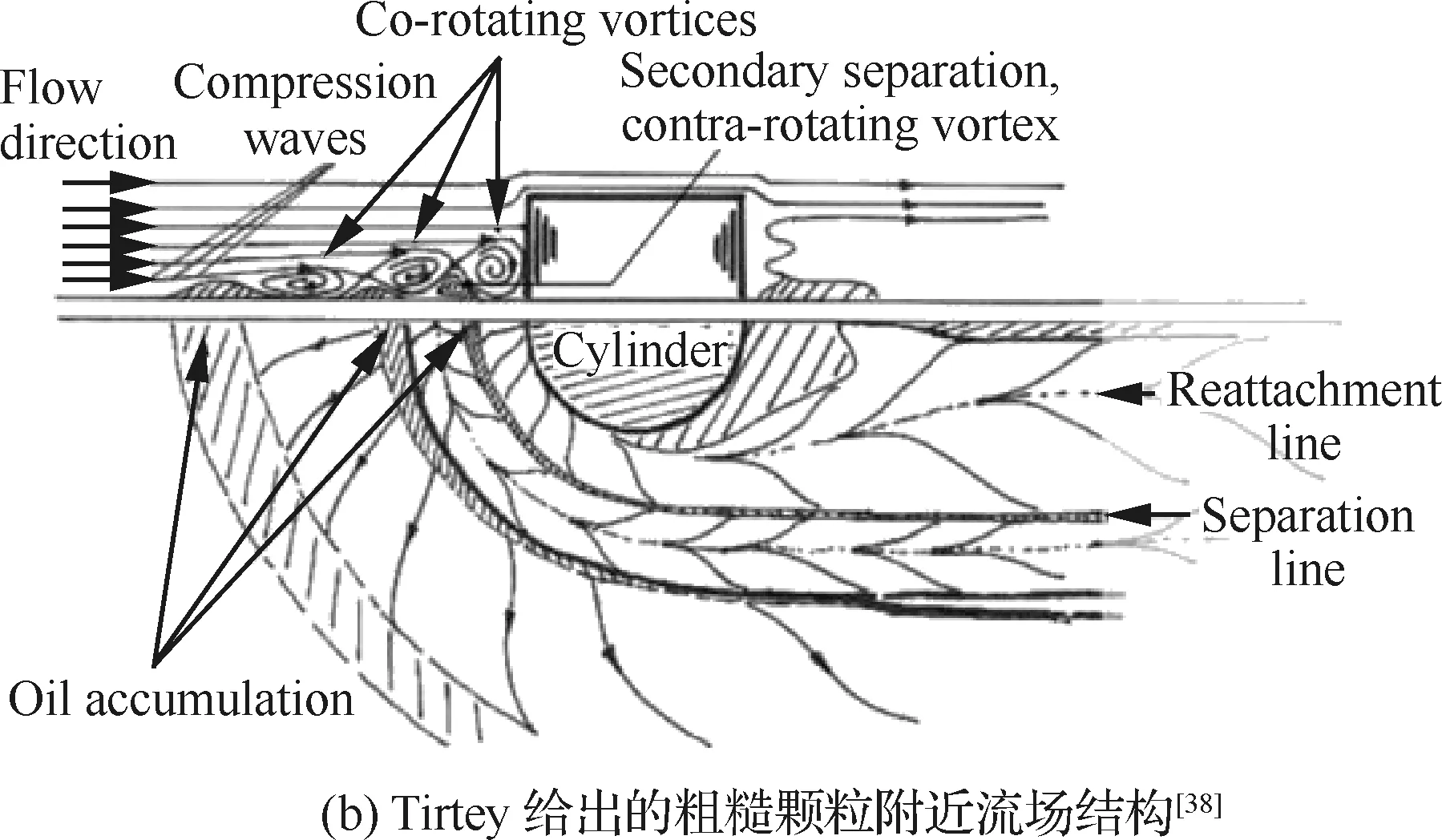
图14 粗糙颗粒附近流场结构Fig.14 Flow field structure around roughness element

图15 对称面流场结构Fig.15 Flow field structures on symmetry plane

图16、图17则分别为瞬态流场中不同法向位置的温度分布和不同流向位置流向涡的涡量分布(图中Δx′为不同流向截面与粗糙颗粒中心的距离)。从图中可知，粗糙单元后存在两层剪切层(与对称面上的结果相一致)，上部剪切层很薄，在向下游的传播过程中逐渐扩散到外流并最终因耗散作用而彻底消失。而下部分的剪切层则与粗糙单元两侧的马蹄涡一开始分别各自向下游发展并缓慢扩散，直到三簇涡在展向上越来越靠近并最终开始相互耦合，之后较大的涡结构开始破碎成较小的涡结构，流动变得不稳定，开始变成湍流。在x=120 mm处，即Δx′=60b时，涡结构已经完全破碎，涡量在展向分布趋于均匀，表明此时转捩已经完成，与前面壁面热流系数和对称面速度脉动均方根分布体现的结果一致。

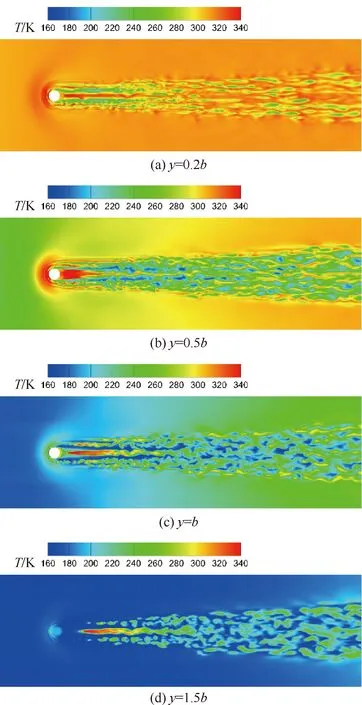
图16 壁面不同法向位置的瞬态温度分布Fig.16 Instantaneous temperature distribution of different vertical distances from wall

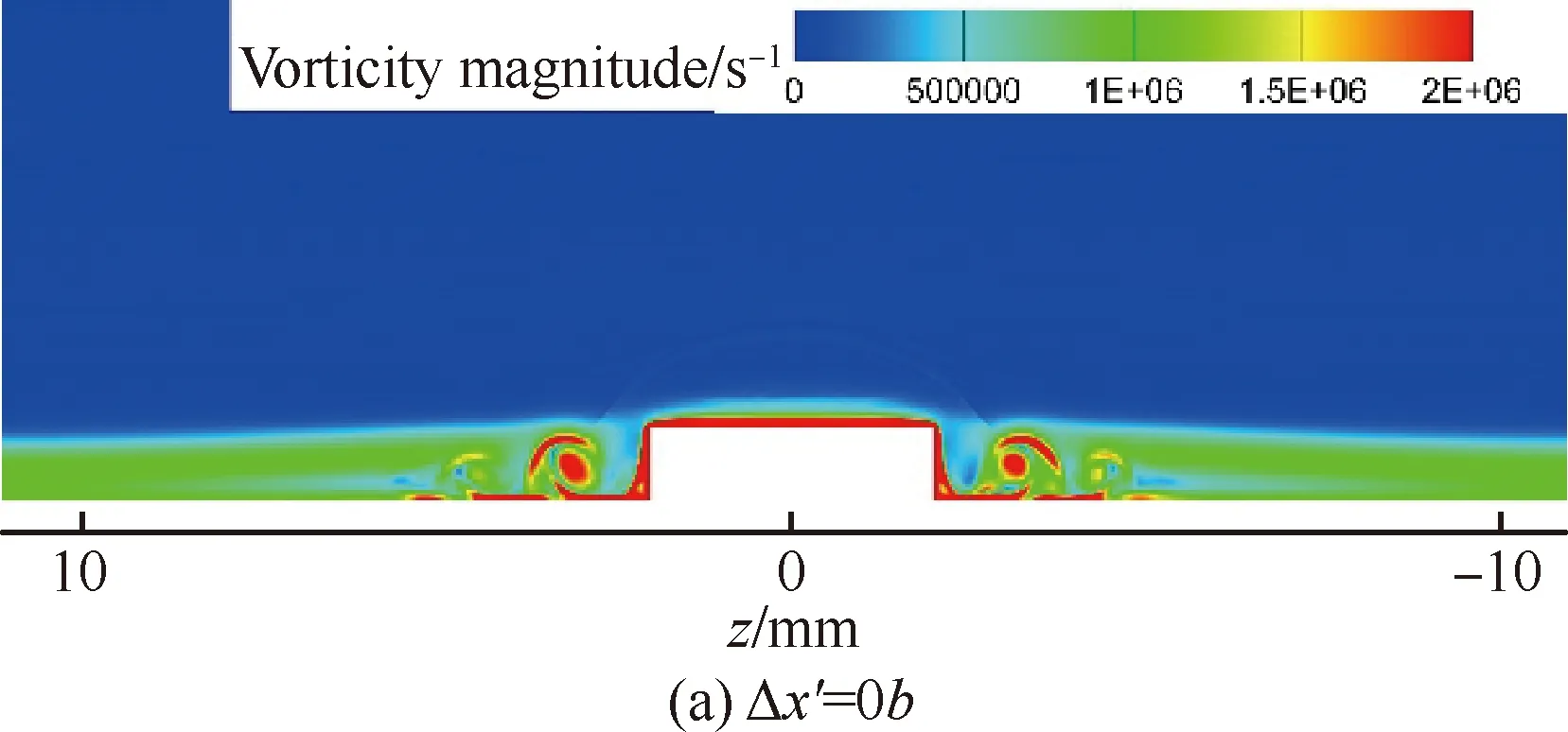
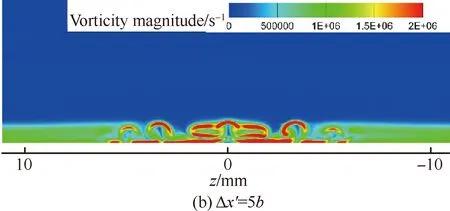
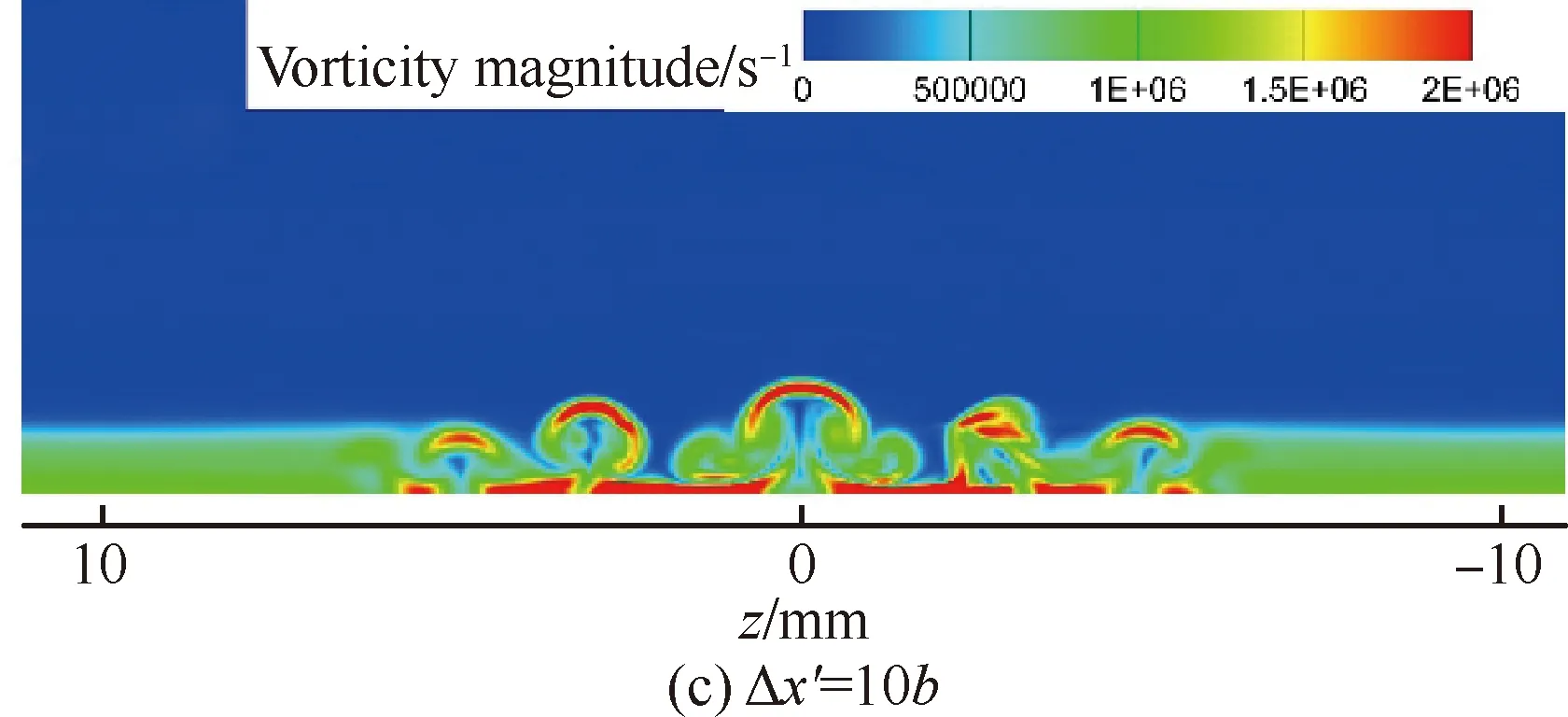
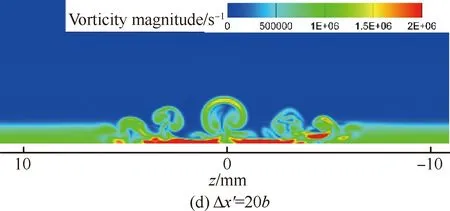
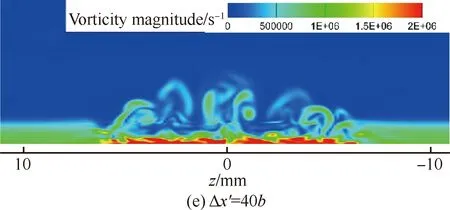
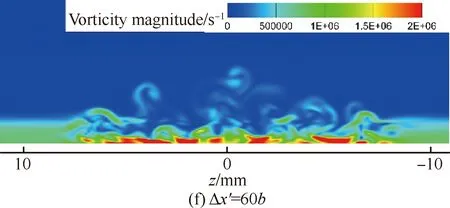
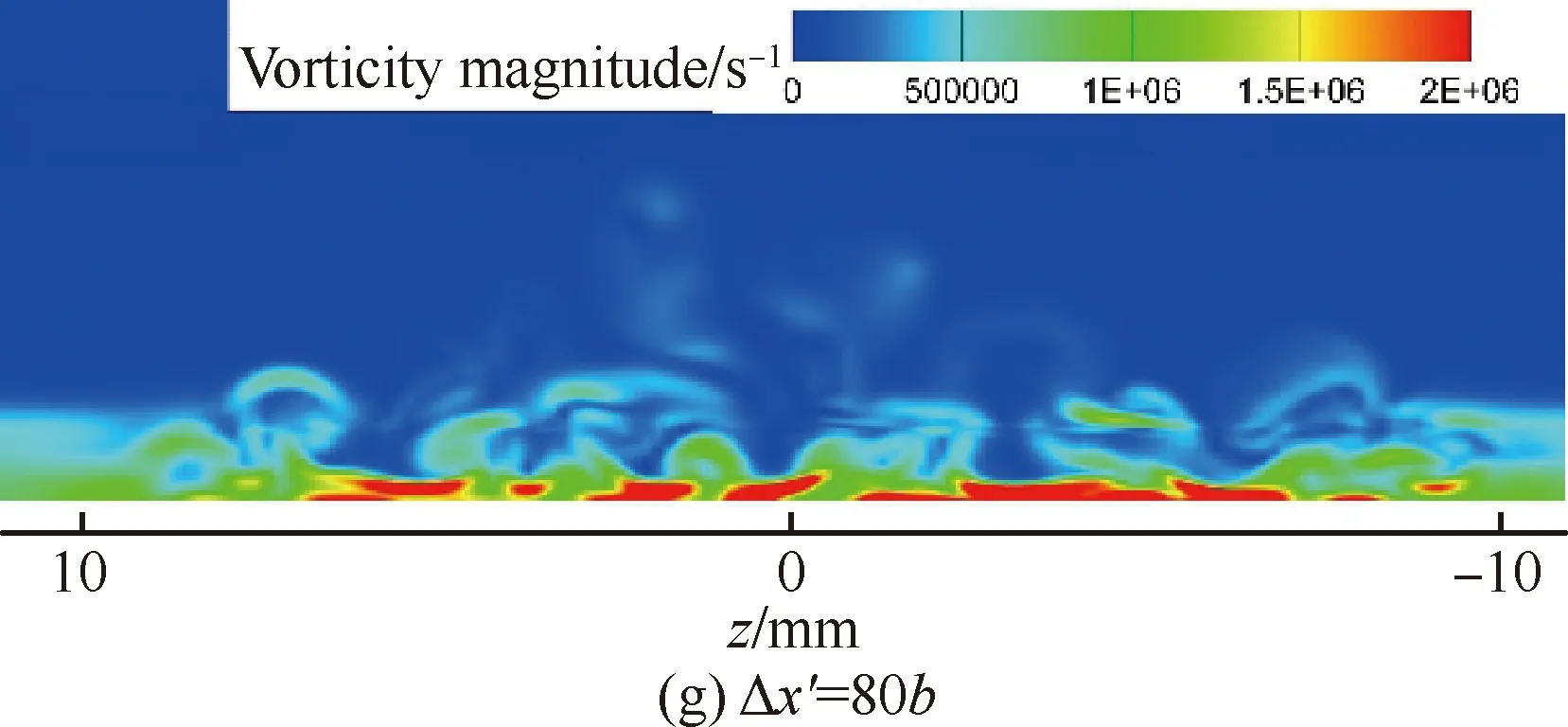
图17 不同流向位置的流向涡涡量云图Fig.17 Streamwise vorticity magnitude contours of different streamwise positions

4 结 论

1)将IDDES方法与γ-Reθ转捩模型结合起来并发挥各自的优势，从而建立形成了新的基于IDDES框架的转捩模型。

2)通过超声速混合层、高超声速自然转捩及粗糙颗粒诱导的强制转捩等一系列算例的计算，表明新建立的方法在模拟自然转捩时，能够像γ-Reθ模型一样通过基于转捩动量厚度的经验关系式得到转捩位置，而在模拟粗糙颗粒诱导的强制转捩时，又能发挥IDDES方法能够捕捉到粗糙颗粒在边界层中诱导出的扰动的特点，能够对粗糙颗粒诱导出的剪切层和马蹄涡结构的形成、耦合和失稳过程进行较为精细地刻画和模拟，从而达到模拟强制转捩的目的。

3)计算结果表明新建立的方法在强制转捩模拟上要优于传统的γ-Reθ转捩模型。