飞机地面轮候时间预测及其算法研究

李连成 乔迪

摘要：飞机轮候时间的预测是飞机推出控制的基础，对于飞机的离港过程具有决定性的意义。通过分析机场离港流程，本文将飞机轮候时间分为跑道起飞等待时间和滑行道轮候时间，基于排队论思想和BP神经网络算法，分别建立了飞机跑道起飞等待队列时间预测模型和滑行道BP神经网络系统，根据某大型机场的数据，对算法进行仿真验证。

关键词：BP神经网络;跑道起飞等待队列;排队论;

1 引言

对飞机轮候时间的精确预测预测一直是飞机地面控制操作过程中的重点问题，对建立合理的调度模型，解决机场地面拥堵问题有着决定性的意义。

针对飞机轮候时间的预测问题，Idris等在构建预测轮候时间的统计回归模型时在前人的基础上，将随机因素纳入考虑范围;Simaiakis基于线性回归的思想，建立了一套队列模型，但此模型使用的数据均来自波士顿机场，因此能较好和波士顿机场能较好拟合，却不适用于其他机场;Gotte等为了得到最小化的飞机轮候时间，综合考虑多种因素例如機场布局、尾流间隔、滑行道限制等多种因素建立了飞机地面滑行及等待过程模型;Rathinam 将机场的平面图抽象为有向图形式，考虑到了飞机离港过程中的各种随机因素，虽没有将机场跑道的容量对于滑行道输出能力的限制纳入考虑范围，所得只部分飞机的局部最优解，但对于其他机场仍具有重要的参考意义。汤新民等分析比较了在封闭机场网络环境，静态和动态路径规划的飞机轮候时间的长短，具有重要的参考价值;陶冶，白存儒等利用遗传算法来优化飞机降落顺序和时间，提高了跑道的利用率。但此模型对于真实体现或模拟飞机地面离港滑行过程还需考证。

基于以上分析，结合排队论的相关知识，构建跑道等待区飞机等待时间预测模型;以BP神经网络的角度和排队论的思想分析滑行道系统，构建滑行道系统的状态转移模型，进而完成对滑行道系统中的轮候时间预测模型的建立。

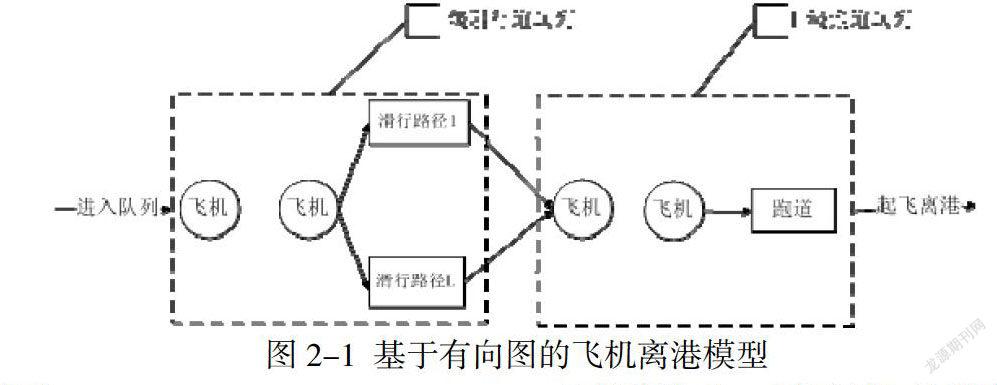
2 飞机地面离港流程分析

本文将飞机离港流程抽象为两级串联系统，第Ⅰ级系统称为滑行道BP神经网络系统，飞机进入滑行道后，虽然大体上可以将其看作神经网络系统，但该系统状态复杂，需要更精确地分析飞机在滑行道系统中的滑行过程以得出模型。滑行道系统实行节点控制，用排队队列来表示各节点的拥堵状态。第Ⅱ级排队系统称为跑道排队系统，是一种典型的FCFS（先进先出）排队等待队列，其队列模型为：M/M/1/K，各字母的含义分别为：M——飞机的间隔时间服从负指数分布、M——飞机服务时间服从负指数分布、1——服务台数目、K——跑道容量。

2.1飞机起飞等待时间预测模型

飞机经滑行道系统以泊松流的方式进入第Ⅱ级跑道起飞等待区等待队列，飞机间的时间间隔服从参数为负指数分布;飞机的服务时间服从负指数分布，设其参数为。

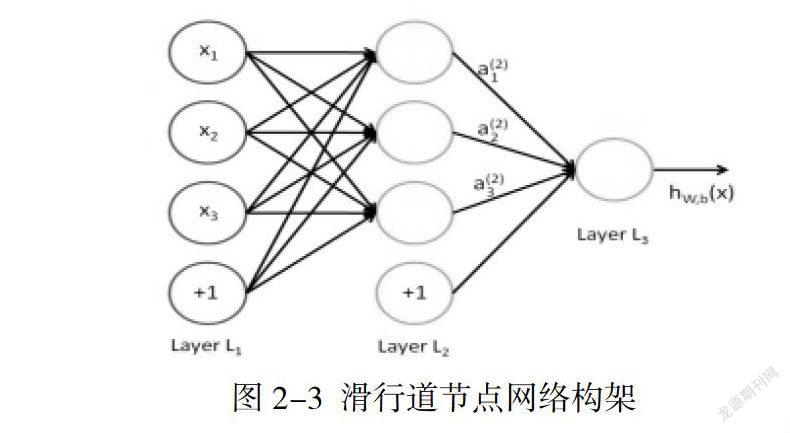
飞机的起飞时间作为输入来到输入层，然后通过与隐层的连接权重，产生一组数据作为节点层的输入，接着通过节点层，即滑行道的激活函数后变为，以来表示节点层的第j个节点产生的输出，但要注意节点层或许并不只有一层，它可以由多架飞机和多个节点组成。在这个过程中，我们将用到排队论的思想构成节点排队队列。再往后将通过隐含层与输出层间的连接权重产生的值作为输出层的输入，接着通过输出层的激活函数，产生输出层第j个节点的输出。

这就是飞机通过滑行道进入跑道起飞等待区的前向传播的过程，隐层本质上也就是特征空间而隐层节点的个数就是特征空间的维数，激活函数一般是S形函数，在本文采用：。将输出层产生的输出与实际值比较，产生误差e，调节权重来尽可能减小误差，以让系统达到较为优化的状态。为了使函数连续可导，这里最小化均方根差，定义损失函数如下：

2.3   节点排队模型

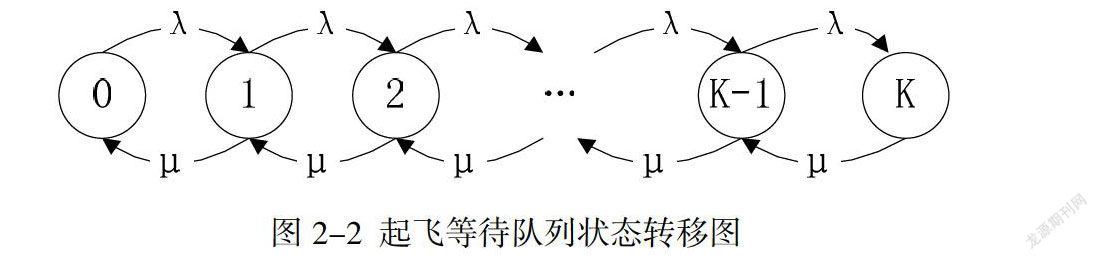
飞机到达每个节点是符合泊松分布的[6] ，故，单节点排队模型为M/M/S/L;模型每个字母的含义依次为：M代表飞机间的时间间隔服从负指数分布，设其参数为λ1;M代表飞机服务时间服从负指数，设其为参数为λ2;S代表节点n可同时服务的飞机数目，L代表节点n的容量。节点n的状态转移形式如下图所示：

滑行道轮候时间如上图3-1所示拟合度很高，而实际的跑道等待时间与计算所得跑道等待时间相差也比较小。因此飞机总的预测轮候时间与实际轮候时间误差很小，预测较为准确。

4结论

本文在对飞机离港流程后，将飞机轮候时间分为跑道起飞等待时间和滑行道轮候时间。经过深入研究后分别构建了跑道等待队列和滑行道BP神经网路。在构建跑道等待队列时，通过对实际数据统计上的研究，确定参数，并进行仿真实验。在构建滑行道BP神经网络时，以排队论的思想构建节点层，从而得到滑行道轮候时间的预测算法，并进行仿真试验。所得的跑道起飞等待时间和滑行道轮候时间与实际数据相比，较为吻合但在允许范围内仍存在一定的的误差。

参考文献：

[1] Anagnostakis，I.，Idris，H.R.，Clarke，J-P.，Feron E.，Hansman R.J.，Odoni，A.，Hall，W.D.，[C] A Conceptual Design of a Departure Planner Decision Aid，presented at the 3rd USA/Europe air traffic management R&D seminar，Naples，Italy，13th -16th June 2000

[2] Simaiakis and h.Balakrishman.Analysis and control of airport departure processes to mitigate congestion impacts [J] Transportation Research Record：Journal of the Transportation Research Board，app.22-30，2010.

[3] Gottle，J.B.，Durand，N.and Alliot，J.M.Handling CFMU Slots in Busy Airport[C].Proceedings of the 5th USA/Europe Air Traffic Management R&D Seminar，Budapest，Hungary.2003

[4] Gottle，J.B.，Durand，N.and Alliot，J.M.etc.Aircraft Ground Traffic Optimization[C].Proceedings of the 4th USA/Europe Air Traffic Management R&D Seminar，Santa Fe，NM，USA.2001

[5] Rathinams，Montoya J，Jung Y.An optimization model for reducing aircraft taxi times at Dallas Fort Worth international airport [C]//26th  International Congress of the Aeronautical Sciences.Anchorage：AIAA，2008：1-14

[6] 湯新民，王玉婷，韩松臣.基于DEDS的A-SMGCS航空器动态滑行路径规划，[J].系统工程与电子技术，2010，32（12）：2669-2675.

[7] 陶冶，白存儒.基于遗传算法的航班动态排序模型的研究[J].中国民航飞行学院学报，2005，8（16）：5-7

（作者单位：1.黑龙江省机场管理集团有限公司扩建工程项目部;2.中国民航大学电子信息与自动化学院）