考虑电机惯量的机器人动力学参数辨识
苏二虎 游玮 江明


摘要:机器人动力学参数的精确辨识对于机器人控制有着重要意义.本文以六自由度工业机器人为研究对象,利用Newton-Euler建立动力学模型,求取辨识最小参数集,以有限项傅里叶级数生成辨识激励轨迹,应用最小二乘法来对机器人进行参数估计,特别地,考虑到机器人高速运动力矩预测问题,在传统的电机力矩加摩擦力矩模型的基础上,将电机与减速机转动惯量加入机器人力矩模型中,通过实验验证模型,表明该模型对力矩有良好的预测效果.
关键词:激励轨迹;工业机器人;参数辨识;力矩模型
中图分类号:TP242 文献标识码:A 文章编号:1673-260X(2019)05-0039-04
工业机器人是一种广泛应用在制造工业领域,集机械、控制、计算机、人工智能等跨学科先进技术于一体的高端制造业中的智能装备.随着近几年工业的发展,工业机器人相关领域日渐成为研究热点[1-3].而机器人动力学参数辨识又是一个非常重要的研究方向,其结果构成了对机器人进行精确控制的基础.一般由CAD软件为基础的原件测量法可得出机器人惯性参数,但由于生产制造和加工组装等原因,此方法难以达到所需精度要求.研究表明[4-6],基于参数辨識理论的机器人参数辨识方法是最有效的途径.
本文以六自由度机器人的动力学参数辨识为研究目标,采用有限项傅里叶函数[7]生产各关节激励轨迹,并以机器人各关节位置、速度、加速度范围作为约束条件,确保生成的轨迹满足机器人实际运动范围,并优化轨迹;通过离线辨识的方法,获取机器人各轴力矩,运用最小二乘法对实验数据进行参数估计;最后运行辨识轨迹,验证方法的正确性.
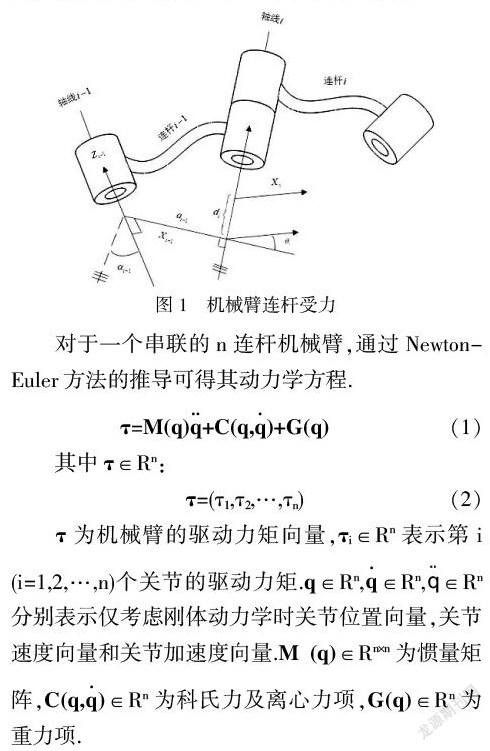
1 六自由度机器人动力学建型
对于机器人动力学建模,比较常用的方法主要有Lagrange方程[8]和Newton-Euler方程[9].由于牛顿欧拉法计算量小,算法高效,可用计算机进行迭代运算,对于很多工业控制器来说,是理想的建模方法,因此本文采用Newton-Euler法建立模型.
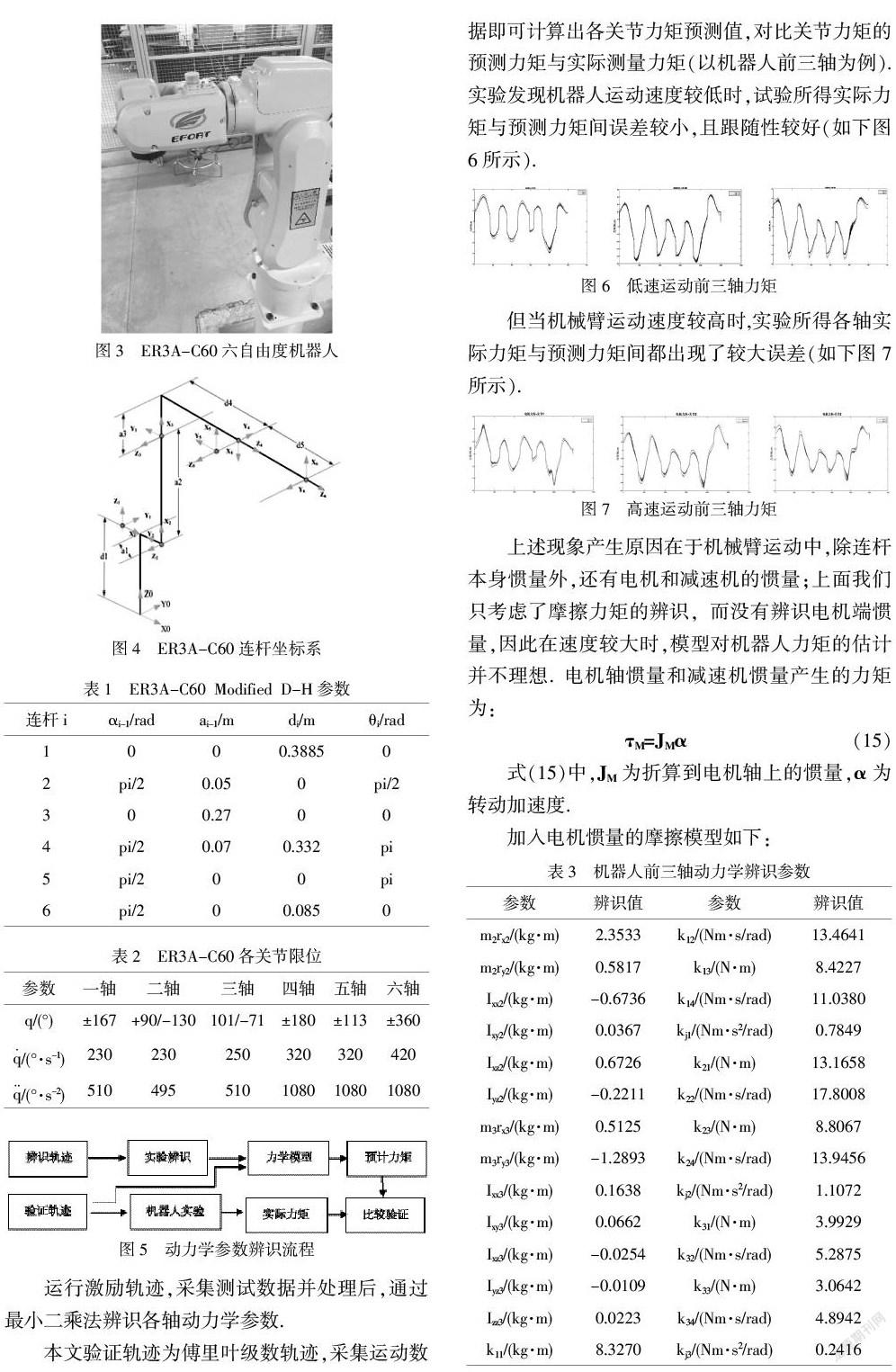
由上述实验结果(图8、表4所示)可以看出使用修改后的动力学模型所得到的各关节预测力矩对测量力矩有较好的跟随性,且基于本文力矩模型得到的预测力矩相对更加准确,误差更小.
4 结论
本文研究了六自由度工业机器人动力学模型辨识方法.首先建立了动力学模型,求取动力学辨识最小参数集,并设计了基于最小条件数的优化激励轨迹,应用最小二乘法来对机器人进行参数估计;特别地,在传统的电机力矩加摩擦力矩模型的基础上,将电机与减速机转动惯量的机器人力矩模型中;以ER3A-C60机器人为实验对象,选取验证轨迹验证模型和预测力矩的正确性.结果表明本文研究的工业机器人参数辨识方法能够正确辨识出机器人的动力学参数,计算出机器人关节力矩并提高了辨识的整体精度,从而达到对机器人精确控制的目的.
参考文献:
〔1〕赵杰.国产机器人的发展现状与挑战[J].机器人产业,2018(05):82-85.
〔2〕陈浩.工业机器人及智能制造发展现状分析[J].现代经济信息,2018(17):360.
〔3〕谭民,王硕.机器人技术研究进展[J].自动化学报,2013,39(07):963-972.
〔4〕陈柏,管亚宇,吴洪涛,谢本华,丁亚东.采用ABC算法的关节机器人动力学参数辨识[J].南京航空航天大学学报,2017,49(05):736-743.
〔5〕黎柏春,王振宇,Alexey Demin,于天彪,王宛山.一种改进的机器人动力学参数辨识方法[J].中国工程机械学报,2015,13(05):381-387.
〔6〕Qin Z K, Baron L, Birglen L. A new approach to the dynamic parameter identification of robotic manipulators[J].Robotica,2010,28(4):539-547.
〔7〕J. Swevers,C. Ganseman,J. De Schutter,H. Van Brussel. Experimental robot identification using optimized periodic trajectories [J]. Mechanical Systems and Signal Processing,1996,10(5).
〔8〕Sheu, S.-Y., Walker, M.W.. Basis sets for manipulator inertial parameters[P]. Robotics and Automation, 1989. Proceedings., 1989 IEEE International Conference on,1989.
〔9〕Atkeson C, An C H, Hollerbach J M. Estimation of inertial parameters of manipulator loads and links[J]. The International.
〔10〕Gautier M. Numerical calculation of the base inertial parameters of robots[J]. Journal of Field Robotics, 1991, 8(4): 485-506.
〔11〕Pfeiffer, F., Holzl, J.. Parameter identification for industrial robots[P]. Robotics and Automation, 1995. Proceedings., 1995 IEEE International Conference on,1995.
〔12〕Calafiore G, Indri M, Bona B. Robot dynamic calibration: Optimal excitation trajectories and experimental parameter estimation[J]. Journal of robotic systems, 2001, 18(2): 55-68.

