数学应用在中职数学教学中的实践

罗启明

摘要：本文通过情景应用题讲解，把数学很好地与专业理论进行了结合，不但提高学生理解专业知识的能力，还促进了学生综合运用数学知识的能力。

关键词：数学应用;实践

中职学校数学作为一门基础性学科，不但要为学生的继续发展打下基础，还要为专业学科的学习作好铺垫服务于专业理论的学习，因此在教学中要由原来单一的、纯数学的教学理念转变为应用性的、综合数学的教学理念。为了在中职学校更好地实践数学在专业学科中的应用，推动课堂教学改革，促进中职学校学生学习数学的自信心和提高综合运用数学知识的能力，本文结合自身的教学实践，阐述和探讨数学在专业学科中应用性教学的实践模式。

本人通过教学实践体会到：要做到数学应用与专业内容的统一，必须采取合适的教学模式，才可取得较好的应用性教学效果。

一、工具数学的应用性教学。

这适用于利用数学的某一方面知识，作为专业理论的研讨工具的数学应用性教学。对于这类应用性教学本人采取“提出问题情景——数学内在联系——数学与专业学科联系——数学应用拓展、解释”的模式进行教学。

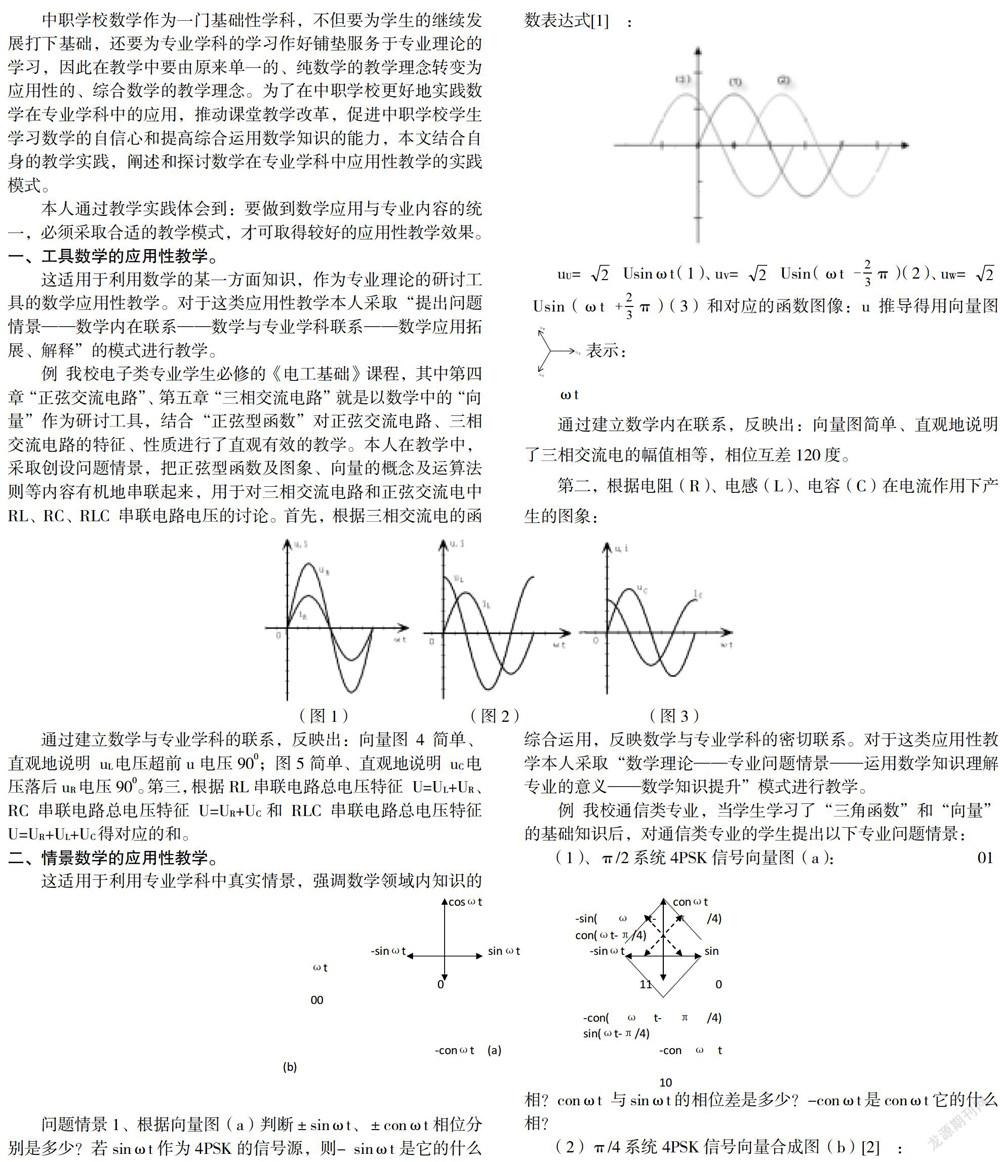
例 我校电子类专业学生必修的《电工基础》课程，其中第四章“正弦交流电路”、第五章“三相交流电路”就是以数学中的“向量”作为研讨工具，结合“正弦型函数”对正弦交流电路、三相交流电路的特征、性质进行了直观有效的教学。本人在教学中，采取创设问题情景，把正弦型函数及图象、向量的概念及运算法则等内容有机地串联起来，用于对三相交流电路和正弦交流电中RL、RC、RLC 串联电路电压的讨论。首先，根据三相交流电的函数表达式[1] ：

uU=  Usinωt（1）、uV=  Usin（ωt π）（2）、uW=  Usin（ωt π）（3）和對应的函数图像：u推导得用向量图表示：

ωt

通过建立数学内在联系，反映出：向量图简单、直观地说明了三相交流电的幅值相等，相位互差120度。

第二，根据电阻（R）、电感（L）、电容（C）在电流作用下产生的图象：

（图1）             （图2）              （图3）

通过建立数学与专业学科的联系，反映出：向量图4简单、直观地说明 uL电压超前u电压900;图5简单、直观地说明 uC电压落后uR电压900。第三，根据RL串联电路总电压特征 U=UL+UR、RC串联电路总电压特征 U=UR+UC和RLC串联电路总电压特征  U=UR+UL+UC得对应的和。

二、情景数学的应用性教学。

这适用于利用专业学科中真实情景，强调数学领域内知识的综合运用，反映数学与专业学科的密切联系。对于这类应用性教学本人采取“数学理论——专业问题情景——运用数学知识理解专业的意义——数学知识提升”模式进行教学。

例 我校通信类专业，当学生学习了“三角函数”和“向量”的基础知识后，对通信类专业的学生提出以下专业问题情景：

（1）、π/2系统4PSK信号向量图（a）：                01

问题情景1、根据向量图（a）判断±sinωt、±conωt相位分别是多少？若sinωt作为4PSK的信号源，则- sinωt是它的什么相？conωt 与sinωt的相位差是多少？-conωt是conωt它的什么相？

（2）π/4系统4PSK信号向量合成图（b）[2] ：

问题情景2、可以看到4PSK信号的每一个向量都可以由两个相邻π/4的向量（用虚线表示）合成。当的向量为con（ωt -π/4），的向量为sin（ωt -π/4）时，那么、的向量分别是多少？

解  情景1  ±sinωt、±conωt相位分别是0、π、和;若sinωt作為4PSK的信号源，则- sinωt是sinωt的反相;conωt 与sinωt的相位差是900，-conωt是conωt的反相

由于学生利用已学数学知识看懂了（a）图的意义，也就非常容易地理解了这（C）原理图的含义。

情景2  利用反向量定义得：、的向量分别为- con（ωt -π/4）、- sin（ωt -π/4）。

由此学生运用已学的数学知识非常容易看懂专业课本中的图表，并能较快地理解和接受专业知识。通过情景应用题讲解，把数学很好地与专业理论进行了结合，不但提高学生理解专业知识的能力，还促进了学生综合运用数学知识的能力。

三、思维训练的应用性教学。

英国哲学家培根说过：“数学是思维的体操”。逻辑思维作为数学的一项基本能力训练，不但体现在数学的实践方面，还贯穿于平时的数学活动和数学学习当中。本人通过“数学活动——数学学习”模式进行这方面的教学。

在数学活动方面：（1）.组建数学兴趣小组进行数学在专业学科中应用的探究，培养学生思维能力。这是一个由理论到实践的思维体验过程，学生通过收集信息，加深理解知识内容，促进学生思维的应用能力。（2）、通过“学期小结”形式，培养学生思维能力。这是一个由学生利用课外时间参与应用性教学活动的环节，它提供让学生动脑、动手的空间和时间，通过课余的观察、体会、分析、概括，培养学生逻辑思维能力;通过思考、对比，促进学生学数学的自信心。

在数学学习方面：（1）.倡导独立归纳单元小结，培养学生思维能力。这是一个由实践到理论的思维体验过程，学生通过梳理已学知识，分析、归纳、建立网络，形成良好知识结构，促进学生思维发展能力

（2）.重视习题课、复习课，培养学生思维能力。这是一个由知识概念的理解和应用，培养思维敏捷性的体验过程。如在进行二次曲线和排列组合的应用的复习（或习题）课教学中，不仅要注意对定义的真正理解，还要突出数学思想、方法的启示。解题时善于观察、联系、分析综合、抽象概括，以达到训练学生思维敏捷性，提高学生逻辑思维和逻辑分析能力。

教学模式的运用是一个继承与发展的过程，也是一个不断创新的过程。构建创新教育的教学模式是教学改革的需要，根据我校所设专业对数学知识的内容有所不同，应该把数学更好地与各专业学科融合。因此设想以“模块式教学”模式进行数学教学实践，使数学更紧密地贴近专业、融入专业，更好地促进学生综合运用数学知识和理解专业学科的素质的全面提高。

参考文献：

[1] 、《电工基础》 薛 涛  高等教育出版社  2001年7月  第117页。

[2] 、《数字通信技术》 王均铭 杨元廷 电子工业出版社2005年1月 第64页。

[3] 、《数字通信技术》 王均铭 杨元廷 电子工业出版社2005年1月 第64页。

（作者单位：惠州工程职业学院）