在初中数学教学中如何培养学生的发散性思维能力

刘永龙

[摘  要：初中数学发散性思维是创新学习必备的思维能力。培养发散性思维能力有利于提高学生学习的主动性、创新性。我们要通过多角度训练，创设相关问题情境，营造积极的学习氛围来培养学生思维的灵活性和主动性，促进学生思维多层次、多方位发散。

关键词：初中数学;培养;发散性思维;一题多解]

心理学认为，创新思维有赖于发散性思维。培养学生的发散性思维能力是数学教学的主要目标之一。因此，数学教学应注重对学生发散性思维的培养。培养学生的发散性思维可以提高学生思考的主动性和积极性以及思维的灵活性。笔者通过多年的教学实践和思考、总结，认为应从六方面培养学生的发散性思维能力。

一、营造愉悦的发散性思维情境，大胆开放教学过程

数学教学中教师应以训练学生创新能力为目的，发散学生思维为根本，保留学生自己的空间，尊重学生的爱好、个性，平等、友善对待学生，学生与老师共同参与教学活动中，让学生做学习的主人，形成和谐的教学环境。只有在和谐的教学环境中，学生才能充分发挥自己的才智和能力。

组织课堂讨论是一种普遍使用的教学方法，这种方法培养出来的学生敢于提问题、敢于质疑，思维敏捷，不受老师讲解的束缚，有利于学生之间的多向交流，取长补短。学生在轻松的环境下，畅所欲言，学生敢于发表独立见解，或修正他人的想法，将几个想法组合为一个最佳的想法，从而培养了学生的发散性思维能力。如在探索《三角形全等》的条件时，我大胆让学生主动探索和发现，在学生分析、研究问题时，我始终参与他们的分析与讨论，听取他们发表新意见，提出新见解，尊重学生差异，充分解放学生的创造力和想象力，为各层次的学生创造性思维能力的培养提供足够的理想空间。这种开放的教学过程，为学生发挥聪明智慧提供了很大的空间，培养了学生的创新精神和实践能力。

二、培养发散性思维时切勿忽视“双基”

首先，要加强数学基础知识的教学和基本技能的训练。学生掌握的知识、技能要准确无误和具有良好的巩固程度，要理解知识间的纵横联系，把握形式与实际的关系。如果在数学基础知识上有这样或那样的缺陷，当学生的思维方式向各方面发散时便会时时受阻。其次，要帮助学生掌握一些解决问题的思想方法和数学方法，如对应、还原、假设、转化、等量代换等，这为他们遇到具体问题时提供了多种途径的解决办法。

三、注重从语言表达上来培养学生的发散性思维

很多学生在传统教育思想的影响下，对于见过的题型能够轻松的解答出来，但是只要遇到一些新颖的题型，学生就丈二和尚摸不着头脑了，说明学生的思维方式缺乏一定的变通性。教师可以试着从语言表达上提高学生的解题变通能力。例如，教师可以采用不同的语言表达方式来描述数学的概念，或者教师让学生用自己的语言阐述一些数学公式、定理、公理等。总之，就是希望通过语言的变化刺激学生的解题变通能力，要学会把知识点融入到自己的知识架构中，进而培养发散性思维能力。

四、激励学生“联想、猜想”，培养学生的发散性思维能力

数学家发现数学规律的过程，往往是先有一个猜想，而后对猜想进行验证或修正的过程，而猜想往往以联想为中介。这类题目不仅题型新颖，而且扩大了学生知识和能力的覆盖面，通过题目所提供的结构特征，鼓励、引导、启发学生大胆猜想，充分发挥他们的想象能力。例如《多边形内角和与外角和》定理的学习探讨，教师可以引导学生从三角形、四边形等特殊图形内角和与外角和定理的探讨入手，启发学生经过一个顶点画对角线，将多边形分成若干三角形出发探讨内角和，从而得出猜想。

五、一题多解是培养发散性思维的重要手段

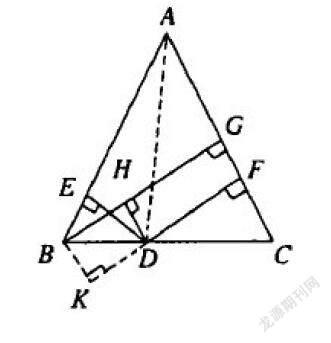
发散性思维是变通的，对一些有代表性问题的解决，教师要充分利用学生学过的知识和技能，调动一切做题手段，从各个侧面论证同一命题的真实性、正确性。通过分析比较，让学生知道哪种方法更灵活巧妙，具有思维的敏捷性、灵活性;哪种方法更呆板沉繁，具有思维的局限性。教师通过一题多解的分析训练，让学生在普遍性中寻求规律性，融数形结合等数学思想、数学思维于一体，优化解题方法，拓宽解题思路的广度和深度。例如，已知ΔABC，AB=AC，D是底边BC上任意一点，DE⊥AB于E，DF⊥AC于F，BG是AC边上的高，求证：DE+DF=BG（如下图）。

分析提问：

（1）这是属于哪一类题型的几何证明题（线段和差问题）。

（2）常用证明方法是什么？（截长补短法）

（3）可采用怎样的方法來证明？（添加辅助线）

（4）怎样添加辅助线？（过D点画DH⊥BG）

（5）需要运用哪些性质来证明？（全等三角形性质和矩形性质）。从学生实际出发，由易到难循序渐进地教给学生分析问题、解决问题的思维方法。

（6）还有别的添线方法吗？（引导学生思维简单发散求异，分析出过B点作FD的垂线交FD延长线于K。在学生掌握了分析问题的方法后，教师引导学生从不同角度、方向探索思路，抓住各部分知识点的联系，一题多解，发散求异。）

六、改变传统的习题教学模式

在传统的数学习题教学中，往往是学生根据既定的条件来寻找结论。为了培养学生的发散性思维，我们改变传统的习题教学模式。例如，让学生把条件和结论倒转过来，根据结论逆向推理出得到这个问题所需要的条件，类似这种逆向思维模式对于提高学生发散性思维非常有利。

七、结语

发散性思维可以使学生思路活跃，思维敏捷，能使学生提出大量可供选择的建议，特别能指出一些别出心裁、完全出乎意料的新鲜见解，使问题奇迹般地得到解决。在初中数学教学中，教师必须立足于“双基”，努力开拓学生的解题思路，在教学意识和方法上注重培养学生的发散性思维，从而切实提高初中数学的教学水平和教学质量。

参考文献

[1]李中恢，黄小洁.数学教学中培养学生发散性思维的实践与研究[J].教学与管理，2007（8）.

[2]周幸宽.浅议在初中数学教学中培养学生的发散性[J].科技创新导报，2009（12）.

[3]麦景雄.在初中数学教学中全面发展学生思维能力[J].农家科技，2011（4）.