小学数学模型思想培养探微

华兵

摘要：数学模型思想比较抽象，对仍以直观形象化思维为主的小学生来说有一定的难度，但可以在日常教学中开展渗透式培养，为学生关键能力和必备品格的形成奠定基础。《因数与倍数》一课教学，从现实生活或具体情境中抽象出数学模型，并用符号、字母等表示出模型，再运用模型解决实际问题。

关键词：小学数学模型思想《因数与倍数》

数学模型，即“把某种事物系统的主要特征、主要关系抽象出来，用数学语言概括地或近似地表述出来的一种数学结构”。小学数学中的数学模型主要有数的概念、计算法则、公式、性质、数量关系等。数学模型思想就是通过对这些数学模型的研究来解决数学问题的一种数学思想方法。数学模型思想比较抽象，对仍以直观形象化思维为主的小学生来说有一定的难度，但可以在日常教学中开展渗透式培养，为学生关键能力和必备品格的形成奠定基础。具体地，可从现实生活或具体情境中抽象出数学模型，并用符号、字母等表示出模型，再运用模型解决实际问题。下面以《因数与倍数》一课教学片段为例加以说明。

一、在具体实例中抽象提取模型

【片段1】

师你能用12个相同的小正方形摆成几种不同形状的长方形？分别说一说你是怎么摆的，并用乘法算式表示出来。

（学生交流摆法和算式：1×12=12、2×6=12、3×4=12。）

师以3×4=12这个算式为例，在数学上我们说3是12的因数，12是3的倍数。能单独说3是因数，12是倍数吗？

生不能。因数与倍数是指两个数之间的关系，所以一定要说清楚哪个数是哪个数的因数，哪个数是哪个数的倍数。

师你能再把另外两个乘法算式像这样说给你的同桌听吗？

（学生交流。）

师观察刚刚用小正方形拼长方形时得到的三个算式，有什么共同的特点？

生都是乘法算式。

生都是自然数的算式。

生积都是12。

师那说明这些都是12的因数。12还有其他因数吗？5是不是12的因数？

生不是，因为5×2.4=12，2.4不是自然数。

师所以在研究因数与倍数时，所指的数一般都是非0的自然数。（稍停）请同学们自己想一个算式，并说一说谁是谁的因数，谁是谁的倍数。

（学生交流。）

师你们在举例时都依据了什么？

生（同步上台板演并说明）我们想到的是（）×（）=（）。第一个乘数和第二个乘数就是乘积的因数;乘积就是第一个乘数的倍数，也是第二个乘数的倍数。

小学阶段因数与倍数概念的教学不能完全从数学抽象的意义上展开，而要通过若干例子，指出两个非0自然数之间存在因数与倍数的关系，从而体会因数与倍数概念。所以这里让学生充分举例，总结发现两个非0自然数之间的关系，从而在具体实例中抽象、提炼出因数与倍数的数学模型——（）×（）=（）。

二、在图示和辨析中解读、理解模型

【片段2】

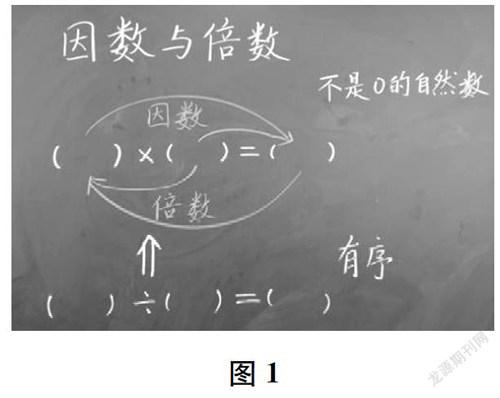
师刚才他们的发言大家都明白了吗？（同步板书，见图1）我们再画一些箭头，就更容易理解了。

图1

（教师出示如下判断题。学生判断后交流。）

1. 因为3×1=3，所以3是3的倍数，3也是3的因数。（）

2. 因为3×5=15，所以3是因数，15是倍数。（）

3. 因为8÷2=4，所以2是8的因数，8是2的倍数。（）

4. 因为10×3.2=32，所以10是32的因数。（）

师第3题你是怎么想的？

生因为除法是乘法的逆运算，所以可以将除法转化为乘法。8÷2=4可以转化为4×2=8，那么就可以得到2是8的因数，8是2的倍数，所以这题是对的。

师也就是说，因数与倍数的背后总能找到相应的乘法算式或者除法算式。

模型刚抽象、提取出来，一部分学生还没有充分理解，这就需要教师在这一难点处放慢脚步，带领学生解读、理解模型。这里，首先通过板书，让学生重点看图中箭头，理解因数与倍数之间的关系;然后通过判断题，加深学生对模型正向和反向的理解。

三、在问题解决中应用深化模型

【片段3】

师那任意给你一个数，你能找到它的所有因数吗？比如36，先独自想一想，然后全班交流。

生只要两个数乘积等于36，那么这两个数就都是36的因数。

生我有补充。只要想（）×（）=36，填进算式的两个数就是36的因数。

生用除法也可以，可以想36÷（）=（），括号里的两个数就是36的因数。

师同学们真棒！用我們之前的乘法算式“模板”，就简便地找到了36的因数。那36最小的因数是多少？最大的呢？

生因为（非0的）自然数最小是1，且符合算式，所以最小的因数是1，那么，最大的因数就是36。

师我们继续来研究一个数的倍数。以3为例，你能找出3的所有倍数吗？

生只要找3乘几，用3和（非0的）自然数相乘，积就是3的倍数。

生只要从3开始，后面依次加3，得到的数就是3的倍数。

生我想到的是3×（）=（），从1开始乘自然数，乘出的结果就是3的倍数。

师这三位同学想的方法都很好！其中第三位同学又想到了一个乘法算式。看来，乘法算式在找一个数的倍数时，也是至关重要的。

师3的倍数还有什么特点？

生根据算式3×（）=（），因为自然数有无穷多个，所以3的倍数也有无穷多个。

师那有最大的3的倍数吗？

生没有。

师最小的呢？

生（非0的）自然数中1最小，根据算式，3的最小的倍数是3×1=3。

师也就是3本身。看来，同学们学得都很好，那让我们来做个小游戏吧！老师这里有个神秘的数，并且和这里的六张牌上的数字有关，这些数字都是从小到大排列的，你能根据这些牌找出这个神秘的数吗？

生（自信地）能！

师那我们来试试看吧。如果这些牌上的数字都是这个数的因数。你认为你只要翻开哪些牌，就能找出这个数？

生只要翻开最后一张，因为一个数最大的因数是它本身。

师如果不允许翻开最后一张呢？

生翻开第二张和第五张，或者第三张和第四张，因为它们的乘积就是这个数。

师如果这些牌都是这个数的倍数，只要翻开哪些牌，就能知道这个数？

生只要翻开第一张，因为一个数最小的倍数就是它本身。

生翻开第二张也行，因为第二张是这个数的2倍，只要除以2就知道了。

生翻开任意一张都可以，只要拿这一张除以它的位置（序数），都能得到这个数。

在学生建构、理解模型之后，通过猜卡片数字的游戏，引导学生应用模型。特别是找一个数的倍数，学生不仅想到第一个数就是要找的数，而且知道原因（最小的倍数就是数本身），还知道翻开任何一张牌都能找出这个神秘的数。这正是“（）÷（）=（）”模型已深深扎根在学生心中、融入学生知识结构中的最好表现。

参考文献：

[1] 顾泠沅.数学思想方法[M].北京：中央广播电视大学出版社，2004.