紧扣图形的核心本质特征

董文彬

摘要：图形内容的教学应紧扣图形的核心本质特征。圆的核心本质特征包括圆的普遍存在性、广泛对称性、各点均匀性以及“以直代曲”“化无穷为有限”的曲线研究方法。小学数学《圆》这个单元的教学，应该设计相应的问题，驱动圆的学习，调动学生的知识经验，促进学生的思维碰撞，引导学生对圆达到最核心、最本质的认识与理解。

关键词：《圆》广泛对称各点均匀转化思想极限思想

“图形与几何”是小学数学的重要内容。无疑，图形内容的教学应紧扣图形的核心本质特征。只有这样，才能促进学生更深刻地认识图形，进而发展学生的空间观念和高阶思维。那么，《圆》这个单元的教学如何做到这一点呢？

一、圆的核心本质特征分析

在小学阶段学习圆，最重要的是认识什么？我认为，应该是圆的三个特性和一种研究方法。

（一）圆的普遍存在性

在现实世界中，从建筑、图案设计到天体、粒子运动，圆的模型几乎是无处不在的。而作为思维对象的圆因其思维特征体现为高度与完全的抽象、纯粹，又只存在于数学世界里。

（二）圆的广泛对称性

其一，圆是轴对称图形，并且有无数条对称轴，任何一条直径所在的直线都是圆的对称轴。其二，圆是旋转对称图形，并且具有任意的旋转不变性，绕圆心旋转任意角度都映射到自身上。从这个角度来看，圆是所有平面图形中最“和谐”的一种图形。

（三）圆的各点均匀性

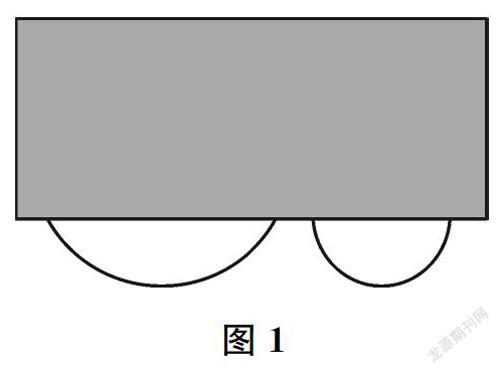
圆的各点均匀性是指圆上任意一点到圆心的距离都相等（即“一中同长”），圆上每一点附近的弧的向心（即弯曲）程度都一样（由图1可以很好地看出圆上一段弧的弯曲程度）。可以说，圆上的每一点都是“平等”的。

图1

（四）圆的曲线研究方法

圆是学生数学学习中第一个认识的曲边平面图形。用直线逼近曲线，用有限逼近无限，这种“以直代曲”“化无穷为有限”的数学方法（如图2示例）贯穿于所有曲边平面图形的学习中。而这种转化与极限的思想也是学生最难理解的。

图2

如果说圆心、半径、直径等是圆的外在“相貌”的话，那么圆的普遍存在性、广泛对称性、各点均匀性和“以直代曲”“化无穷为有限”的研究方法就是圆的内在“性格”。在实际教学中，教师要特别重视让学生感受圆的这种内在“性格”，逐步积累研究曲边图形的经验。

此外，在《圆》这个单元的后续教学中，学生还要学习圆的周长和面积以及实际应用等内容。认识了圆的上述“性格”，才能够更好地探索圆的周长和面积的推导过程和方法，以及圆的实际应用问题的解决过程和方法。同时，关注这些过程和方法，可以引导学生经历图形转化、对应关系等诸多思考，从而有助于学生对圆的核心本质特征的再认识。

二、问题驱动圆的学习

为了帮助学生深刻地认识圆的核心本质特征，教师可以设计相应的问题，驱动圆的学习，调动学生的知识经验，促进学生的思维碰撞，引导学生对圆达到最核心、最本质的认识与理解。下面举例说明。

（一）驱动圆的广泛对称性的学习

对于圆的广泛对称性，学生需要在平时的教学中不断经历想象、操作的学习活动，在比较中深刻认识圆的这种区别于其他图形的本质特征。

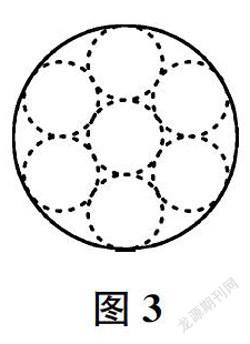
问题1请在图3的大圆中描出一个或几个小圆，使原来的大圆和描出的小圆组成的新图形分别满足“有无数条对称轴”“只有一条对称轴”“只有两条对称轴”“只有三条对称轴”。分別应该怎样描？

图3

此题可以驱动圆的轴对称性的学习。学生需要思考多个圆组合在一起时对称轴数量的变化情况，对圆的轴对称性产生新的认识。

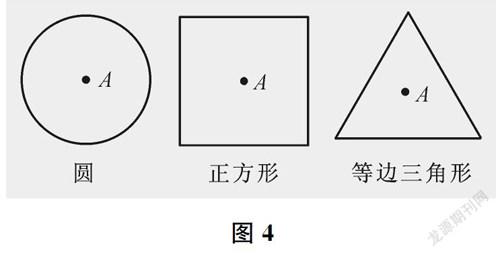
问题2图4中的圆、正方形和等边三角形标出了中心点A。想象将它们分别绕着中心点A转动，每个图形至少旋转多少度才能与原来的图形重合？每个图形在旋转一周的过程中与原来的图形重合了几次？

图4

此题可以驱动圆的旋转对称性的学习。学生通过想象与操作可以发现：正方形至少旋转90°才能与原来的图形重合，等边三角形至少旋转120°才能与原来的图形重合，而圆旋转任意一个角度都可与原来的图形重合;正方形旋转一周会与原来的图形重合4次，等边三角形旋转一周会与原来的图形重合3次，而圆旋转一周可与原来的图形重合无数次。

（二）驱动圆的各点均匀性的学习

对于圆的各点均匀性，学生也需要在观察、想象、操作、思考、比较中体会圆的这种区别于其他平面图形的本质特征。

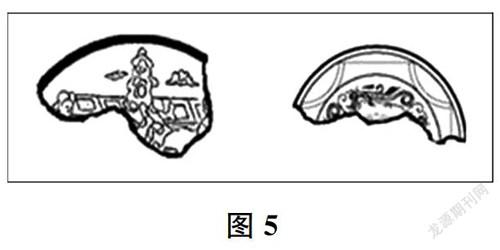
问题3图5所示是两块不同的圆形铜镜边缘的残片。对比这两块残片，哪块铜镜的面积更大？

图5

此题可以驱动圆的各点均匀性的学习。学生可以借助对圆的特征的理解，通过具体操作（延长外圆）找到圆的半径，或者通过感性思考（空间想象）还原圆的整体，或者通过理性思考（看弧度：圆越大，弯曲的程度就越小;圆越小，弯曲的程度就越大）来解决。

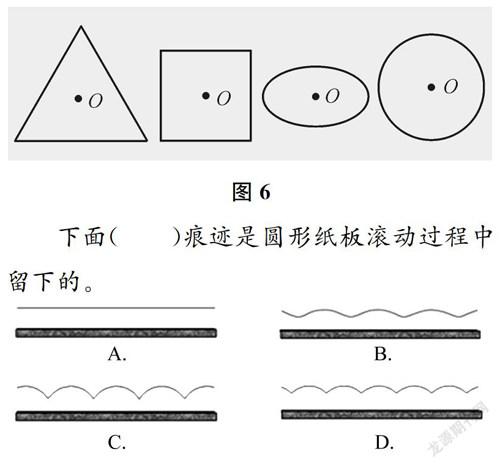
问题4有图6所示的几种形状的硬纸板。将这几块硬纸板分别沿一条直线滚一滚，描出滚动过程中O点留下的痕迹。

图6

下面（）痕迹是圆形纸板滚动过程中留下的。

此题可以驱动圆的“一中同长”特征的学习。学生需要想象不同图形的中心在运动中的高低变化，重点理解为什么圆心的运动痕迹是直线，进而体会圆区别于其他平面图形的核心本质特征——圆心到圆周的距离是圆的半径，同一个圆的半径是相等的。在运动过程中，圆心到滚动面的距离一直等于半径，所以圆心的运动痕迹是一条直线。这也从数学的角度解释了“为什么车轮是圆的”。

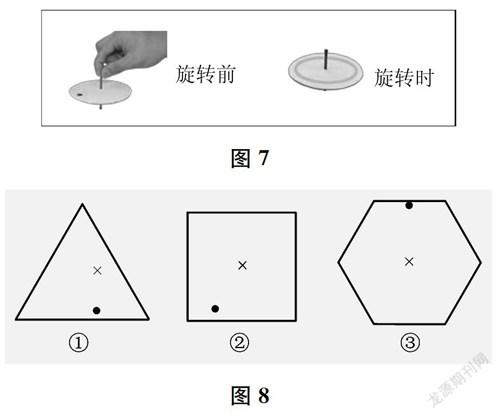
问题5在自制的陀螺上点一个黑点，在陀螺旋转时，黑点便可以形成一个圆形的痕迹（如图7）。淘气也自制了几个陀螺，并点上了黑点（如图8，“×”标出的是插入旋转轴的地方）。其中哪个陀螺在旋转时，黑点可以形成一个圆形的痕迹？

图7

图8

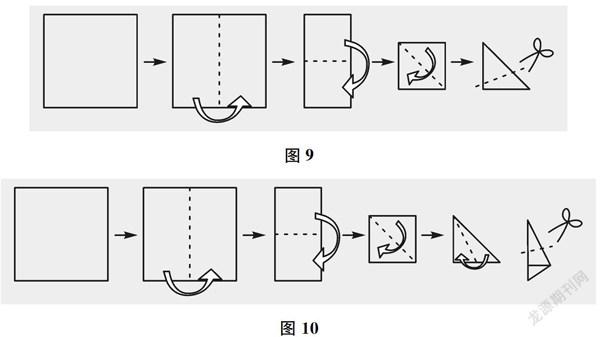
此题也可以驱动圆的“一中同长”特征的学习。学生可以在想象、操作中，感悟圆的定点、定长，体会只要给一个定点，那么以一定长度为距离旋转一周所形成的封闭曲线就是圆，即圆是到定点的距离等于定长的所有点的集合。图9

图10

（三）驱动圆的曲线研究方法的学习

对于圆的曲线研究方法，学生需要基于有限情况下的操作，展开无限情况下的想象，逐渐由“动手”转向“动脑”，从而领悟“以直代曲”“化无穷为有限”的思想。

问题6如图9，用一张正方形纸这样折叠三次后，沿虚线剪出一个等腰三角形，打开后的图形接近圆。如图10，用一张同样大的正方形纸这样折叠四次后，沿虚线剪出一个等腰三角形，打开后的图形也接近圆。上述哪一种方式剪出的图形更接近圆呢？

此题可以驱动圆的曲线研究方法的学习，让学生感悟正多边形边的条数越多，图形越接近圆，体会正多边形逼近于圆的转化与极限思想。

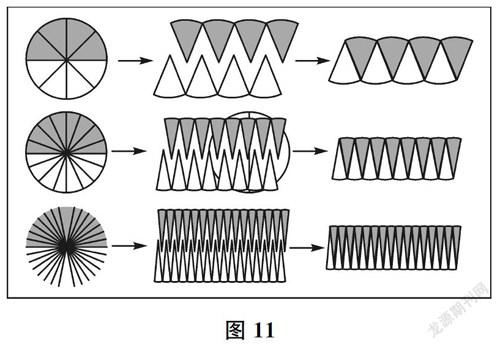
问题7将一个圆形纸片沿着它的半径平均分成若干份后剪开，用它们可拼成一个近似的平行四边形（如图11）。已知这个平行四边形的周长是16.56厘米，那么这个圆形纸片的面积是（）平方厘米。

图11

此题可以驱动圆的面积公式推导过程中图形转化时对应关系的学习。学生需要根据平行四边形相邻两条边的长度分别对应圆的周长的一半和圆的半径，以及圆的周长和半径的关系，反向算出圆的半径，进而计算圆的面积。教师在教学过程中，要引导学生将圆尽可能多地等分，同时想象转化后的情况，然后启发学生思考：为什么要尽可能多地等分？在图形转化的过程中，什么变了？什么没变？如果学生能够体会到在这个过程中圆的周长增加，面积守恒，形状不断趋近于长方形，那么，他们对转化与极限思想的理解就算有了一定的深度了。