小学数学教学中“相异构想”的破除






摘要:在正式学习有关知识之前,学生头脑里并非一片空白,而是通过对日常生活中一些现象的观察和体验,形成了一些前概念和相异构想。在教学《平行四边形的面积计算》一课之前,对学生进行前测,发现他们普遍存在相异构想:平行四边形的斜边越长,面积就越大;平行四边形的面积=底边×邻边。据此展开针对性教学:不暗示,暴露真实认知;不跨越,基于认知发展;不回避,破除相异构想。
关键词:相异构想学情调查针对性教学《平行四边形的面积计算》
众所周知,在正式学习有关知识之前,学生头脑里并非一片空白,而是通过对日常生活中一些现象的观察和体验,形成了一些非科学的概念和特有的思维方式。专家们将这类概念称为前科学概念(简称为“前概念”),将围绕前概念建立起来的错误思维结构称为“相异构想”。教学研究和实践说明:错误不会轻易被正确覆盖,它影响着一个人学习行为的理性趋向,阻碍着正确知识的接受。从这个角度来看,教学的核心意义在于破除学生的相异构想。
具体到《平行四边形的面积计算》一课,学生在正式学习平行四边形的面积计算之前,有没有相异构想?如果有,达到了什么程度?如何针对性地进行教学?
一、学情调查
在教学《平行四边形的面积计算》一课之前,我对任教的两个五年级班级的78名学生进行了前测(测试题如下页图1),来调查他们关于平行四边形面积计算的学情。
1.下面每组中两个图形的面积相等吗?如果相等,请在中间画“√”;如果不相等,请圈出较大的图形。
2.你能通过测量所需的数据,计算下列图形的面积吗?(单位:厘米)
第1题中,前两组图形都是等底等高的图形,它们的面积相等;第三组图形中的平行四边形是由长方形沿对角拉成的,长方形的面积较大。
第2题中,两个图形各边的长度都严格按照勾股定理设计(如图2),确保学生不会因测量数据不是整数而对计算方法产生怀疑。
学生第1题的答题情况如表1所示(其中,“答题结果”为左边图形相较于右边图形的大小关系)。可以看出, 67.9%的学生将第一组中的平行四边形“想”大了,83.3%的学生将第二组图形中左边的平行四边形“想”大了,57.6%的学生将第三组图形中的平行四边形“想”大了,即:学生对平行四边形大小(面积)的判断明显受斜边的影响,而且斜边相对于高倾斜的角度越大,产生的偏差就越大。
学生第2题的答题情况如表2所示(其中,“典型错误”指的是采用“底边×邻边”的方法,“其他错误”指的是除了“典型错误”以外的测量出错、计算出错、没完成等情况)。可以看出,运用“底×高”计算的学生不足20%,而运用“底边×邻边”计算的学生却达到了惊人的65.4%。
综合可以推知,在正式学习平行四边形面积计算之前,学生普遍存在相异构想:平行四边形的斜边越长,面积就越大;平行四边形的面积=底边×邻边。通过前测了解到的学情是学生学习的真正基础,理应成为教学设计和课堂教学的起点。
二、针对性教学
(一)不暗示,暴露真实认知
【教学片段1】
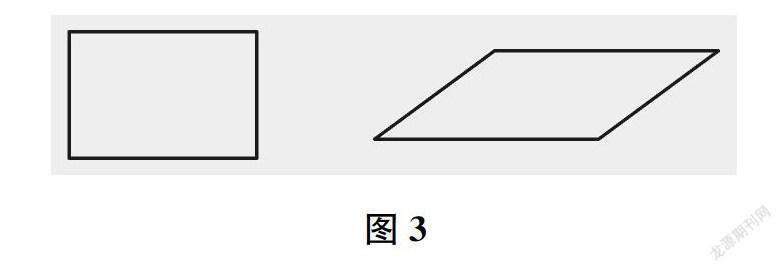
师(出示图3)下面哪个图形的面积大?
生平行四边形的面积大。
生长方形的面积大。
师观察不出来,我们拿起来比一比。
(学生拿出教师提供的卡片比较。)
生一样大。
生平行四边形面积大。
师看来争论还不小。要想准确地比出它们的大小,我们可以量一量,算一算。现在请同学们量出需要的数据,用厘米作单位,算出它们的面积。
生我量出了长方形的长是6厘米,宽是4厘米,面积就是6×4=24(平方厘米)。
师同学们有没有问题?
生(齐)没有。
生我量的是平行四边形的底和右斜边,底是7厘米,右斜边是5厘米,7×5=35(平方厘米)。
师同意这种方法的请举手。
(有很多学生举手。)
师同意的还不少嘛!你们为什么这么想?
生把这个平行四边形拉一下,就会变成长方形。按照长方形的方法做,就可以了。
(学生拉伸可活动的平行四边形框架,明确拉伸后得到的长方形的长和宽分别对应原来平行四边形的底和斜边。)
师有不一样的做法吗?
生我量出了它的底和高,底是7厘米,高是3厘米,7×3=21(平方厘米)。
师答案不一样了,你支持哪一种?
……
为了充分展示学生的原始想法,教师精心设计了两个图形:舍弃等底等高的组合,避免暗示学生用切割、平移的方法去转化;长方形和平行四边形的面积尽量接近,并且各边长都是整数厘米。同时,汇报的次序及方式也很有考究:先汇报多数人使用的“底边×邻边”方法,并通过操作活动加以“强化”;而对“底×高”的方法,只呈现算法,不阐述道理。学生无法从教师的语言中得到提示,便会充分暴露真实认知。
(二)不跨越,基于认知发展
【教学片段2】
师要比较面积,我们之前学过一个很有效的办法是——
生数方格。
师请同学们拿出方格纸,数数看。
(学生利用方格纸数平行四边形的面积。)
生21。
生我也数出来是21。
师大家都是21。你们是怎么数出来的?
生我是先数整块的,然后把小块的拼一拼,加起来就是21平方厘米。
(教师同步多媒体操作,如图4所示。)
生我把左边一整块的三角形全部移到右边。
(教师同步多媒体操作,如图5所示。)
面积计量的本质,其实就是用面积单位对计量对象进行计数。数方格是基础而切实有效的计量面积方法,也是面积公式推导中可以利用的基本经验之一。由于平行四边形的性质,数方格时出现了不是整格的情况。生活中“化零为整”的经验可以帮学生找到解决的方案:把不满一格的零散小格拼成一个整格来计数。在有些教师看来,跳过数方格活动,直接进行抽象推导或许更快捷、更彻底。但儿童的数学学习不是一蹴而就的,它是一个缓慢的、循序渐进的过程,必須建立在儿童已有的知识基础和生活经验之上。不跨越,尽最大可能地激活儿童的已有经验,并据此开展学习活动,才是儿童数学学习的应有之道。
(三)不回避,破除相异构想
【教学片段3】
师通过数方格,我们知道了平行四边形的面积能用“底×高”来计算,这是什么道理?
生(指图5)沿着高剪开后,把左边的三角形平移到右边,只是位置发生了变化,大小是不变的。
生长方形的长就是原来的底,宽就是原来的高,利用长方形的面积公式,平行四边形的面积=“长”ד宽”=底×高。
师那之前很多同学使用的“底×邻边”的方法,为什么不能用呢?
生拉成长方形后,面积变了。
师变大了,还是变小了?
生变大了。
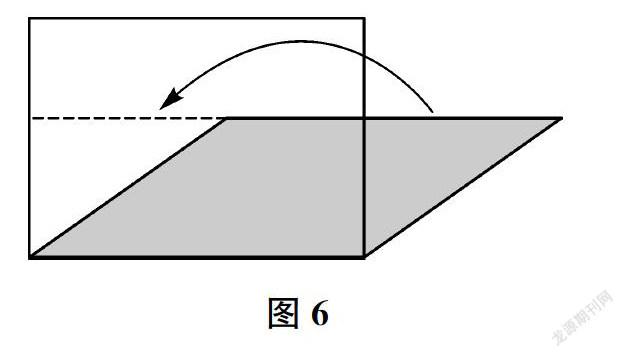
生(同步上台操作,如图6所示)把右边的三角移到左边后,上面还会空出一块,这一块就是变大的面积,所以不能用这种方法。
平行四边形的面积为什么是“底×高”?为什么不是“底边×邻边”?通常,我们会非常重视前者,忽视后者。部分教师甚至“谈异色变”,担心这种“异”会使学生对周长、面积的认识产生混乱。事实上,教学避而不谈,学生就不乱了吗?按照知识的内在逻辑进行教学固然可取,但部分学生很难真正理解。他们会认为新学的知识“似乎有些道理”,但他们也坚信原来的认识“有道理”,于是两种观念混合,造成认知结构的模糊。这里,教师引导学生探究“底×邻边”方法的错误原因,破除“平行四边形变形成长方形后面积不变”的相异构想。
参考文献:
[1] 薛正桧.儿童相异构想的成因及破解之道[J].江西教育,2018(8).
[2] 郑可菜.基于“相异构想”的课堂教学法初探——从哈佛公开课说起[J].教育研究与评论(中学教育教学),2014(2).
[3] 顾志能.教学,贴着学生的思维前行——“平行四边形的面积”教学实践与思考[J].小学数学教育,2012(Z1).

