初中数学三角形专题复习例题解析

柯孙长

摘要：三角形是初中阶段重要的数学知识点之一，同时也是中考的考点，能够与代数知识紧密联系在一起，对提高学生逻辑思维十分有益，因此深受广大数学教育工作者高度重视。在本篇文章中，笔者就初三阶段如何更好地开展三角形专题复习，进行例题解析。

关键词：初中数学;三角形;专题复习;例题解析

三角形作为中考数学中重要的考查点，受到广大师生的关注，很多教师在复习过程中将三角形作为专题进行复习，希望能够引导学生将所学习的关于三角形的知识点汇聚到一起，并且熟练掌握三角形解题方法和技巧，提高复习效率。

一、三角形的内角和例题解析

众所周知，三角形内角和为一百八十度。很多学生在做题前都已经完全掌握了这一概念，但是中考中仍旧将之作为基本考查点，使其在识记这一结论基础上，能够熟练应用它的另外三个推论。数学教师在带领学生复习三角形内角和时一定要紧密结合一些例题，使得他们学会应用所学三角形内角和知识点解答数学问题。

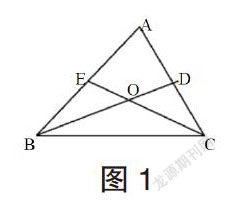
例题一：如图1所示，已知ABC是頂角大小为60度的一个三角形，其中线段BD和线段CE分别平分角ABC和角ACB，并且两个线段相交于一点O。求解三角形中角BOC的大小为多少。

解：因为在三角形ABC中∠A=60°，

所以∠ABC+∠ACB=120°;

又因为线段BD和CE分别为∠ABC和∠ACB的角平分线，

所以∠ABD=∠DBC，∠ACE=∠ECB，

所以∠ABC+∠ACB=∠ABD+∠DBC+∠ACE+∠ECB=2（∠DBC+∠ECB）;

又因为∠ABC+∠ACB=120°，∠ABC+∠ACB=2（∠DBC+∠ECB），

所以∠DBC+∠ECB=60°，

所以∠BOC=180°-60°=120°。

二、三角形的平分线例题解析

在初中阶段，三角形中出现了三条重要的线段：中线、角平分线和高，在一些特殊的三角形中这三条线段可能是同一条线段。所谓角平分线，是指将三角形中任意内角平均分成两个相等角的线段，并且与对边交于一点。在三角形中，人们常常还将三个角的平分线的相交点进行了命名，称之为内心。数学教师在带领学生复习三角形的平分线时一定要将这些基本知识点灌输其中，使学生建立起联系，提高其复习效率。

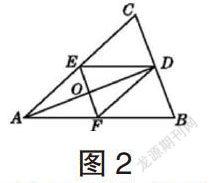
例题二：如图2所示，在三角形ABC中，线段AD将角CAB的平均分成两个等大的角，线段EF与线段AD在点O出出现汇合，且线段DE与AB、线段DF与AC都是相互平行的关系，求证线段DO是角EDF的角平分线。

解：（1）因为线段AD是角CAB的平分线，

所以角EAD等于角FAD;

又因为ED平行于AB和线段DF平行于AC，

所以角EDA=角FAD，角FDA=角EAD，

所以角EDA等于角FAD，

所以线段DO是角EDF的角平分线。

三、全等三角形例题解析

学生在学习全等三角形时除了掌握其概念外，还应该熟记几种证明三角形全等的方法以及学会如何利用全等三角形将问题进行转变，进而提高三角形学习效率。数学教师在带领学生复习全等三角形时，一定要使其学会准确辨认全等三角形所对应的各个条件，掌握综合证明法证明三角形全等的的格式与方法，同时学会发现和利用隐含条件进行转化，条件隐蔽时可添加辅助线用判断定理。

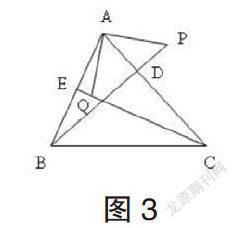
例题三：如图3所示，在三角形ABC中，线段BD和CE为三角形两个高，三角形外存在一点P是高BD延长线上一点，且线段BP的长度与AC长度相等，点Q是线段EC上一点，且线段CQ的长度与AB长度相等，求证线段AP和线段AQ长度相等且互相垂直。

解：因为线段BD和CE均为三角形ABC的高，

所以，角CAE和角ACE的和为九十度，角CAE和角ABD的和也为九十度，

所以角ACE与角ABD相等;

又因为在三角形ABP和三角形ACQ中CQ等于AB、角ACE等于角ABD、AC等于BP，

所以三角形ABP全等于三角形ACQ，

所以线段AP与AQ相等;

又因为角QAC和角P相等、角PAD与角P的和为直角，

所以角PAD与角QAC的和为直角，

即角PAQ为直角，

所以线段AP垂直于线段AQ。

四、直角三角形例题解析

直角三角形是一类特殊的三角形，常常出现在各地中考卷中，是中考热点内容，因此教师在带领学生一起复习这部分内容时既要将基础的直角三角形性质定理以及应用综合性地介绍给他们，还要使其学会熟练使用直角三角形的判定定理解答数学问题。

例题四：如图4所示，在三角形ABC中，其中角C为九十度，角CDA与角CDB角度也为九十度。（1）若三角形中的角A度数为60，那么如何求证线段BD长度是线段AD的三倍;（2）若线段BD长度是线段AD的三倍，那么如何求证角A为60度。

解：（1）因为在三角形ABC中角C为直角，角A大小为60度，

所以角B等于30度，角ACD也等于30度;

又因为角C为直角以及CD垂直于AB，

所以线段AB长度等于2倍AC长度，线段AC等于2倍AD长度，

所以AB等于4倍AD长度，

所以线段BD长度是线段AD的三倍。

将AB的中点标记为O，连接CO，

因为BD=3AD，

所以AB=4AD;

又因为角C为直角，点O为AB中点，

所以OC=AO=BO=2AD;

又因为CD垂直于AB

所以角OCD等于三十度，角COD等于六十度，

所以三角形ACO为等边三角形，

所以角A为60度。

一言以蔽之，广大初中数学教师在带领学生进行三椒香专项复习时一定要将一些典型的例题讲解给学生，使其熟练掌握解题技巧，提高解题效率，并且能够在中考中取得优异的成绩。

参考文献

[1]张忠华.初中数学总复习教学中拓展型问题的设计与思考——以定三角形基架下的动点问题为例[J].上海中学数学，2015（4）：17-18.

[2]万国全.注重能力培养优化二轮专题复习课教学--以“三角形中的最值与范围问题”为例[J].中学数学教学，2016（1）：19-22.