矿井涌水量计算的稳定与非稳定流解析法

张曼曼　姚多喜

摘 要：准确预测矿井涌水量，对煤矿的采掘方案和排水能力的合理设计具有重要意义.以青东煤矿为例，依据单口抽水水位恢复数据，运用泰斯水位恢复理论求出煤系砂岩含水层渗透系数K及贮水系数u*，并将计算结果与稳定流的K值进行对比.在此基础上，运用“大井法”对建井期一水平的矿井涌水量分别进行了稳定流和定降深变流量非稳定流预计.研究结果表明，水位恢复与稳定流理论计算出的渗透系数值相差不大;煤矿建井期实测涌水量总体平稳，稳定流理论计算值与总体均值接近;由于砂岩裂隙发育的不均一性，在局部时段，涌水量呈现疏干递减型，非稳定流理论值与实测值拟合较好;反映出稳定流理论可对涌水量进行总体预测，而非稳定流对部分独立砂岩裂隙水单元可准确预测出涌水量的动态变化规律.

关键词：矿井涌水量;稳定流;非稳定流;解析法

中图分类号：TD742  文献标识码：A  文章编号：1673-260X（2019）11-0092-04

矿井涌水一直都是影响矿安全生产的关键因素之一，给矿井的建设、掘进及开采都带来了一定的困难.而矿井涌水量在煤地质学中则是指流入矿井巷道内的地表水、裂隙水、老窑水、岩溶水等的总量，它是煤矿开采的一个重要技术条件[1-2]，也是制定矿山疏干设计方案、确定生产能力的主要依據，其直接关系着煤矿采掘方案和排水能力设计的合理性，更决定了煤矿是否能够安全生产，因此矿井涌水量的准确预测预报尤为重要.预测矿井涌水量的方法有很多种，一般可包括确定性预计方法和非确定性预计方法两类.确定性预计方法包括解析法、水均衡法、数值法和物理模拟法;而非确定性预计方法主要分为时间序列分析法、模糊数学法、灰色关联法、回归分析法、神经网络法、地质比拟法和混沌模型法等.

实际采矿工程中，解析法又可称为地下水动力学法，由于具有概念清晰、计算简便以及参数易于获取而被广泛地运用在矿坑涌水量的计算中，该法通过合理概化实际问题，构造解析公式从而达到计算水矿区涌水量的问题.经过多年的实践该法已积累较多的工程经验，为正确指导矿井开采合理布置疏排水工程奠定了良好的前期基础.本文以青东煤矿一水平开采涌水量计算为例，分别采用稳定流解析法和非稳定流解析法对其涌水量进行预测，为煤矿排水系统设计与布置提供参考指标.

1 研究区地质概况

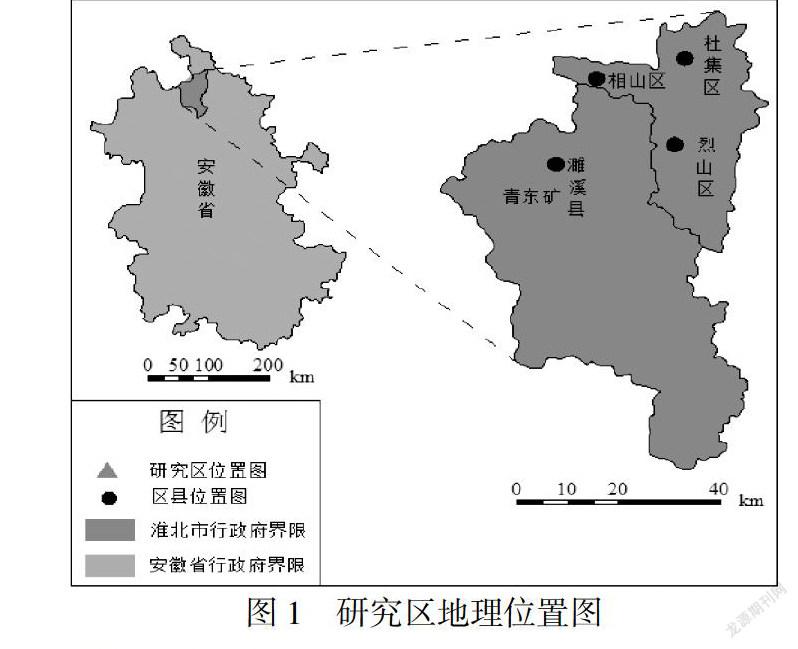
青东煤矿位于安徽省濉溪县临涣镇石集村境内，研究区位置如图1所示.本区属淮河水系.淮北煤田位于安徽北部，是全隐蔽煤田，松散层厚度大，属于华北型地层，主要含煤地层为二叠系的上石盒子组、下石盒子组和山西组，含煤地层平均总厚880.8m.

青东煤矿构造主体表现为一走向北西～近东西，局部略有转折，向北、北东倾斜的单斜.地层倾角一般10～20°，沿走向方向出现较小规模的地层起伏或次级褶曲;井田以正断层为主，局部有岩浆岩侵蚀，构造复杂程度为中等.

矿区内含水层可根据地下水赋存介质特征划分为新生界松散层孔隙含水层、二叠系煤系砂岩裂隙含水层和太原组及奥陶系石灰岩岩溶裂隙含水层，如图2所示.矿井主要充水水源有新生界松散层第四含水层（“四含”）、主采煤层顶底板砂岩裂隙含水层、太灰、奥灰石灰岩岩溶裂隙含水层、老空区积水，这些充水水源都直接或间接的影响着矿井的充水.在掘进和工作面回采时，受采掘破坏或影响主要是各主采煤层顶底板砂岩裂隙含水层，其位于疏干开采的层位，因此，各主采煤层顶底板砂岩裂隙含水层是矿井充水的直接充水含水层.

2 涌水量计算的稳定流理论

2.1 “大井法”简介

工程实践中常用解析法中的“大井法”，即把巷道系统所占面积简化成一个圆形的大井，当矿井排水时，以巷道系统为中心，在矿井周围会形成具有一定形状的降落漏斗，这与钻孔抽水时形成降落漏斗的情况相似，进而可利用地下水动力学公式来计算涌水量.

当承压水头H值降至含水层底板时，h=0，地下水处于承压转无压水流状态，故估算涌水量时采用承压～无压完整井公式.含水层一般为承压含水层，当承压水井进行大降深抽水时，若井中水位低于含水层顶板，井附近则出现无压水流区，这时承压水井就会变成承压无压（潜水）井.

2.2 涌水量计算

2.2.1 计算公式

依据矿区水文地质条件，分析矿井充水水源、通道和强度等因素，可采用稳定流“大井”法预测矿井涌水量，涌水量估算范围是先期开采地段一水平（F6～大刘家断层），浅部以主采煤层露头带为界，深部至-585m水平.按照“大井法”原理，将此开采面积视为一大井，计算时选用承压～无压完整井公式：

式中：Q为矿井涌水量，m3/h;K为渗透系数，m/d;M为含水层厚度，m;S为水位降低值，m;F为采区面积，km2;R0为含水层的引用影响半径，m;r0为“大井”半径，m;r为影响半径，m;H为水头高度，m;h为井筒水柱高度，m.

2.2.2 计算参数

经过现场实测，可得到7～8煤含水层厚度M、估算面积F以及透系数K，将渗透系数K代入式（2），可求出大井半径r0、“大井”引用影响半径R0和影响半径r，具体参数值如表1所示.

2.2.3 计算结果

将上述各个参数代入式（1），可得到7～8煤含水层涌水量Q1=100m3/h.

3 涌水量计算的非稳定流理论

一般来说，稳定流“大井法”预测矿井涌水量，具有快速、简便等优点.但该预测模型只能总体上反映出涌水量的大小，不能反映出涌水量随时间的变化规律，因此本节采用非稳定流理论进行涌水量的动态预测.

3.1 非稳定流计算公式

在矿井排水量大于充水含水层补给量时，在建井过程中，开采初期或开采水平延伸的情况下，地下水的运动始终处于非稳定流状态，无法达到相对稳定的条件，只有用非稳定流法才能客观的计算矿井涌水量.非稳定流计算公式如下：

式中：s离钻井井轴r处的水位降深，m;Q为抽水井的流量;T为导水系数;t为自抽水开始到计算时刻的时间;r为计算点到抽水井的距离;u*为含水层的释水系数;W（u）为井函数.

3.2 计算参数的求取

利用非稳定流定降深法计算涌水量时，需要释水系数u*参数值.理论上讲，在多孔介质骨架的形变为线弹性的情况下，含水层的贮水系数和释水系数应该是相等的，故可利用水位恢复数据计算含水层参数u*，其计算原理如下所示：

如果不考虑水头惯性滞后动态，水井以定流量Q持续抽水tp时间后停抽恢复水位，那么在时刻（t>tp）的剩余降深s’，（原始水位与抽停后某时刻水位之差），可理解为流量Q继续抽水一直延续到t时刻的降深和从停抽时刻起以流量Q注水t-tp时间的水位抬升的叠加.两者均可用Theis公式计算.故有：

利用6-71孔对7～8煤层顶底板砂岩裂隙含水层（段）的抽水试验水位恢复资料，利用软件Aquifer Test中的Theis Recovery进行拟合，6-71孔的拟合曲线图3所示，并可得到该孔的导水系数T为5.4×10-6m3/s.

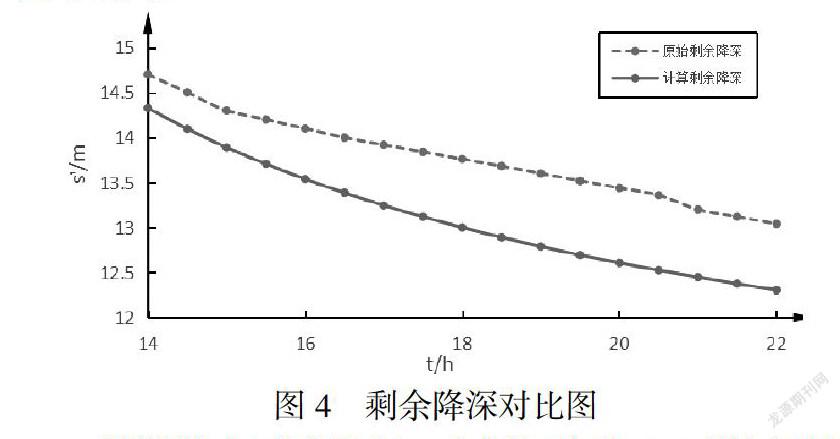
由抽水资料可知6-71孔的涌水量Q为0.286 L/s，停抽时刻的水位降深sp为85.02m，距抽水井的距离为0.055m，将拟合得到的T代入斜率公式可求得i分别为11，将其代入式（8）中可求得a分别为2.38.又根据u*，可以求得7～8煤层顶底板砂岩裂隙含水层的u*为2×10-6.将拟合曲线所求的T代入剩余降深公式，其与原始降深对比曲线图如图4所示.

根據抽水试验资料，可直接得到7～8煤层引用半径r和降深s，而其导水系数T和渗透系数K可由上述拟合曲线求得.由拟合曲线图可知孔6-71测得7～8煤层的K值为0.015m/d，稳定流的7～8煤的K值为K=0.03235m/d，二者结果相差不大，具体参数如表2所示.

3.3 计算结果

该矿目前主采7～8煤，根据开采过程中井下水位观测可知，7～8煤层在35d后水位降到-585m，即一水平处，呈现出疏干现象;如表3所示.将上述参数代入到式（4），可得到不同时间和不同降深情况下的各煤层涌水量，如图5所示.

从图5可以看出，在同一降深下，涌水量随时间的增大而逐渐减小;在相同时间内下，涌水量随降深的增大而逐渐增大.矿井涌水量初期一般比较大，后期随着时间的增加而逐渐减小，但减小的幅度在变小.与稳定流理论相比，非稳定流可计算出涌水量的动态变化过程.

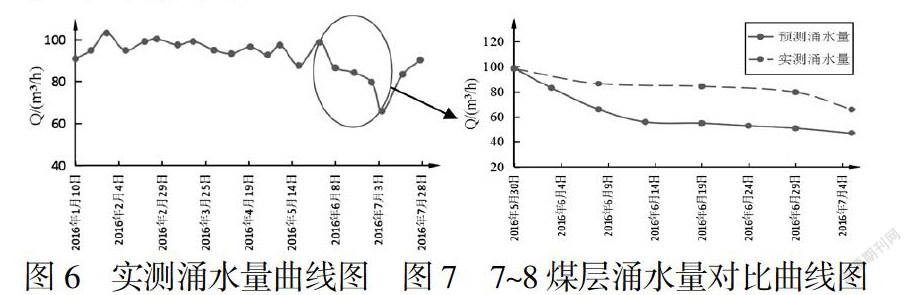
为验证本次水文地质参数求解的合理性，利用本矿7～8煤实测矿井涌水量见图6所示.由图6可以看出，2016年1月～2016年7月矿井涌水量为65.90～103.10m3/h，平均涌水量为92.00m3/h，涌水量总体趋于相对稳定，局部存在波动，与稳定流理论计算出100m3/h吻合程度较高.同时在2016年5月30日至7月5日期间，涌水量呈现递减状态，提示此段为独立砂岩裂隙含水单元的疏干现象，可采用非稳定流泰斯公式计算涌水量的动态变化过程，计算结果如图7所示，从图中可看出，二者吻合较好，反映出由本文确定的水文地质参数精度较高，对涌水量的计算以及含水层水文地质条件的评价具有较好的指导意义.

4 结论

4.1 运用稳定流“大井法”公式估算出先期采掘地段一水平7～8煤顶底板砂岩裂隙含水层Q1=100m3/h，该矿井实测矿井7～8煤涌水量值一般为92m3/h，与稳定流计算值相差不大.非稳定流泰斯计算7～8煤层涌水量在35d后为46.86m3/h，与稳定流预测值相差不大;而非稳定流计算结果反映在揭露部分独立的砂岩裂隙含水层时，其预测的涌水量趋势与实际涌水量趋势相一致.由上表可知，非稳定流预测的矿井涌水量的变化规律一般是前期较大，后来逐渐减小并趋于稳定状态;涌水量随时间和降深增减而发生变化，即在同一降深，涌水量随时间的增大而逐渐减小;在相同条件下，涌水量随降深的增大而逐渐减小.一般情况下，稳定流预测涌水量适用于水文地质条件较为简单的地区，比较理想化;而非稳定流则可利用抽水试验所获取的资料来求取相关的水文地质参数，继而预测矿井涌水量，可准确地反映出涌水量的衰减趋势.

4.2 煤矿建井期实测涌水量总体平稳，稳定流理论计算值与总体均值接近;由于砂岩裂隙发育的不均一性，在局部时段，涌水量呈现疏干递减型，非稳定流理论值与实测值拟合较好;反映出稳定流理论可对涌水量进行总体预测，而非稳定流对部分独立砂岩裂隙水单元可准确预测出涌水量的动态变化规律.

参考文献：

〔1〕崔原萍，张宝平.解析法在矿井涌水量预测中的应用及评价[J].地下水，2016，38（05）：8-9+76.

〔2〕虎维岳，闫丽.对矿井涌水量预测问题的分析与思考[J].煤炭科学技术，2016，44（01）：13-18+38.

〔3〕黄欢.矿井涌水量预测方法及发展趋势[J].煤炭科学技术，2016，44（S1）：127-130.

〔4〕乔美英，程鹏飞，刘震震.基于GA-SVM的矿井涌水量预测[J].煤田地质与勘探，2017，45（06）：117-122.

〔5〕刘启蒙，胡友彪，张宇通，刘浩.矿井涌水量预测方法探讨[J].安徽理工大学学报（自然科学版），2017，37（06）：1-7.

〔6〕刘基，王强民，杨建.基于Visual Modflow的矿井涌水量模拟和动态预测研究[J].煤矿安全， 2018，49（03）：190-193.

〔7〕Lalit Kumar Sahooa，Santanu Bandyopadhyay，Rangan Banerjee.Water and energy assessment for dewatering in opencast mines[J]. Journal of Cleaner Production，2014（84）：736-745.

〔8〕马青山，骆祖江.解析法和数值法在矿井涌水量预测中的比较[J].矿业安全与环保，2015，42（04）：63-66+71.

〔9〕华解明.“大井法”预测矿井涌水量问题探讨[J].中国煤炭地质，2009（6）：45-47.

〔10〕尹尚先，张祥维，徐慧，等.“大井法”中渗透系数及含水层厚度的优化[J].煤田地质与勘探，2015（5）：53-56.

〔11〕刘洋，张幼振.浅埋煤层工作面涌水量预测方法研究[J].采矿与安全工程学报，2010（1）：116-120.

〔12〕施鑫源，阮淼森，王世杰，等.供水水文地质手册[M].北京：地质出版社，1983.

〔13〕华解明.矿井涌水量计算的非稳定流解析法[J].中国煤炭地质，2010，22（10）：38-40.

〔14〕来永伟，孔庆虎，李志慧.非稳定流定降深法在矿井涌水量预测中的应用[J].中国煤炭地质，2018，30（S2）：50-52+78.

〔15〕薛禹群.地下水动力学[M].北京：地质出版社，2010.

〔16〕郭建青，周宏飞，李彦.分析含水层水位恢复数据的多次直线解析法.岩土力学，2008，29（12）：3246-3250.