河岸潜流带中非稳定地下水流的溶质运移模拟研究
郭 昆,李 宁,熊启华,王芮琼,廖春来
(1.湖北省地质环境总站,湖北 武汉 430034; 2.资源与生态环境地质湖北省重点实验室,湖北 武汉 430034;3.中国地质大学(武汉)环境学院,湖北 武汉 430078)
在工农业密集的冲洪积平原,赋存着丰富的孔隙水,且地表水系发育,通常地表水和地下水具有一定的水力联系和相互作用[1],这一相互作用的关键带称为潜流带,它对局部地区的生态环境和水资源起着重要作用。潜流带的地下水往往随着地表水水位的波动存在着与地表水互补的现象,形成非稳定流,因此对于潜流带中的溶质迁移研究一直是个热点,也是难点。杜尧等[2]系统梳理了潜流带的水文和生物地球化学过程的相关原理和研究方法,此外有学者通过实验尺度的数值模拟和室内实验等方法,探究了溶质在潜流带的迁移规律[3-5]。但是这种实验尺度的研究较为理想化,对于实际复杂的水文地质条件的适用性还有待检验,另外以往的研究对象多为河床潜流带,而对范围较大的河岸潜流带的研究较为少见。
地下水溶质运移模型是预测溶质在地下水中运移的有力手段,主要利用数学公式和一些基本条件刻画溶质在地下水中的运动、降解等物理化学过程。模型的主体部分包括控制方程、初始条件和边界条件,它们决定了溶质在研究区的初始状态及其与外界的转换方式。目前溶质运移模型已成功应用到地下水环境影响评价和水污染防治等工作和研究中[6-9]。本文基于FEFLOW软件的地下水溶质运移模型,并以武汉汉江边某污染场地为研究对象,对河岸潜流带非稳定地下水流的溶质运移进行模拟研究。该实例模型探讨地表水—地下水相互补给条件下污染物在承压含水层中的迁移规律,旨在为场地水土环境质量评价及地下水污染治理提供科学依据。
1 研究区概况
污染场地位于武汉市硚口区,处于汉江一级阶地上,地势平坦开阔(图1)。阶地由第四系全新统粉质粘土、粉细砂及含砾中粗砂组成,主要地下水类型为第四系松散岩类孔隙承压水,承压含水层厚约为30 m,其上覆相对隔水层为粉质粘土,平均厚度为11.5 m,下伏隔水层为泥岩地层。区内地下水水位随汉江丰枯水期变化而变化。在丰水期,地表水水位均高于承压水测压水位,在水动力驱动下,一方面汉江水向河岸潜流带补给,使得承压水压力增大,测压水位升高;另一方面存在部分向上越流补给潜水,抬高了潜水位。在枯水期,汉江水位下降幅度大,此时的承压含水层水位高于江水水位,潜水越流补给承压含水层水进而又向汉江排泄[10](图2)。
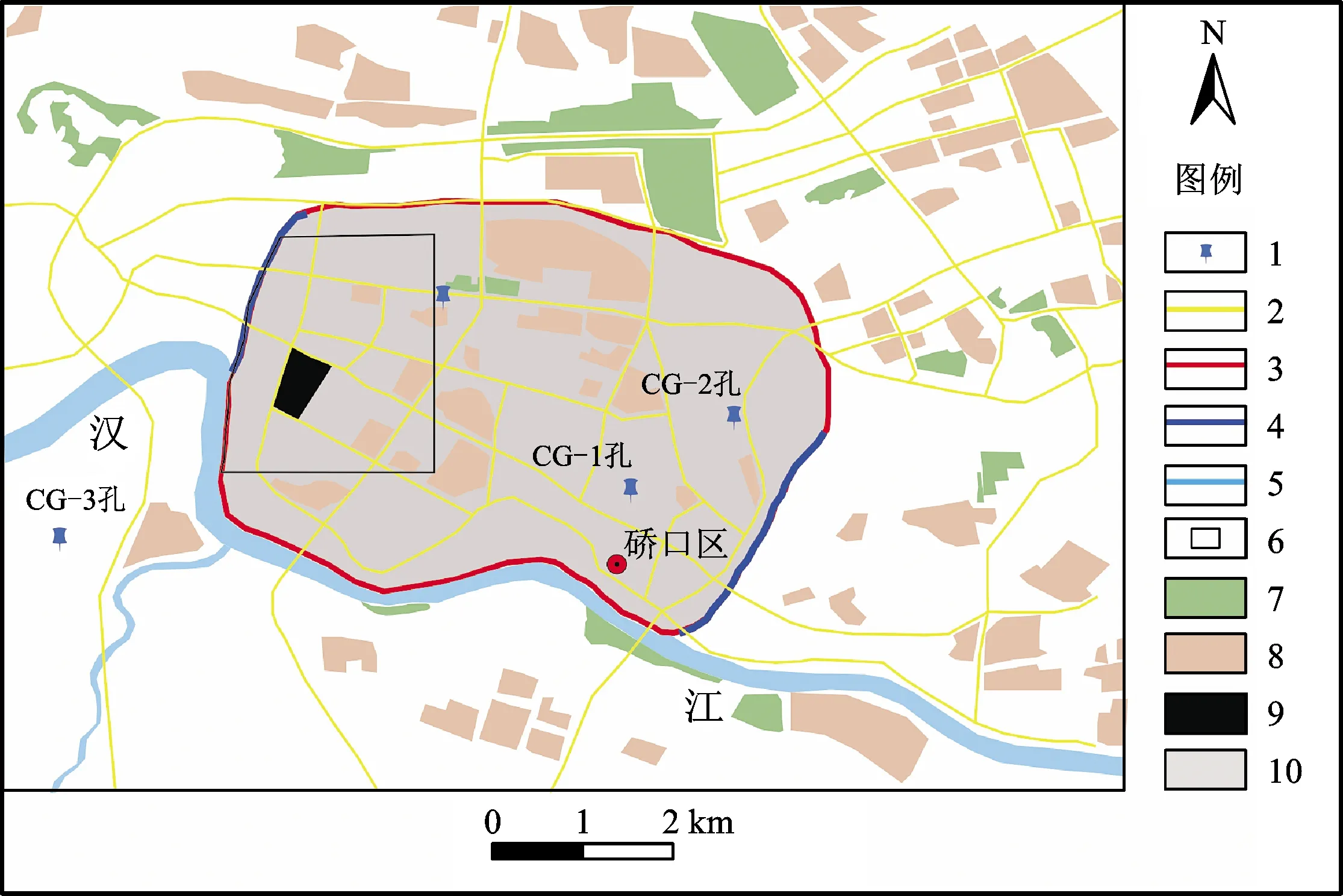
图1 研究区平面示意图

图2 研究区剖面示意图及地表水—地下水水位动态变化图
研究区原为一制药厂,场地主要污染物包括挥发性有机化合物、总石油烃类,以及硝酸盐等无机污染物。通过对厂区钻孔地下水采样分析检测显示,地下水中的挥发性酚类、氨氮、硫酸盐、氯化物等指标较高,达到了Ⅴ类水标准;在场区中心取样进行淋滤实验,结果显示,表层土壤滤出液的硫酸盐、硝酸盐、氯化物的浓度均最高,分别为2 007 mg/L、1 263 mg/L、448 mg/L,均超过地下水质量Ⅲ类标准,说明该场地的土壤包气带和地下含水层均受到了一定程度的污染,影响了城市供水安全和周边的环境健康。
2 地下水流模型
溶质运移的载体是地下水流模型,因此正确的地下水流模型是使溶质运移模型结果可靠、合理的关键性因素。非稳定流溶质运移模拟是在一定的初始流场条件下开始进行的,该初始流场通常取自代表该模拟区地下水系统的稳定模拟结果,它可以来自多个钻孔地下水位的插值,也可以是人为校正后的天然流场,将稳定流模型的边界赋上随时间变化的序列值(本文是汉江水位),运行后便是一种非稳定流。地下水流模型一般包含水文地质概念模型的建立、边界条件和模型校正等过程。
2.1 水文地质概念模型
根据实际的地下水流场并结合场地地质条件,圈划出模拟区面积约21 km2(图1)。模拟区地层由上到下可概化为:杂填土、粉质粘土、粉细砂和泥岩等。杂填土、粉质粘土渗透性较小,模型上将它们归为一层;粉细砂层作为主要的含水层,为第二层;底部的泥岩可不予模拟,系统自动将其作为不透水地质体。最后将模拟区概化成非均质、各向异性、三维非稳定流的水文地质模型。
2.2 边界条件与水文地质参数
模拟区南边以汉江作为给定水头边界,北边作为一个地下水水位基本稳定的边界,概化为15 m水头的定水头边界,东、西两侧作为流量边界处理[11-12](图1),即Q=KIA,由于软件可自动计算A,因此只需将KI输入模型即可,本次模型取I为0.01。上边界主要接受大气降水的入渗补给,根据武汉市多年平均降雨量及入渗系数,模拟区地下水补给净输入设置为12 mm/a,下边界泥岩作为底部相对隔水边界。模拟区初始流场的南部水头边界为汉江2015年7月5日的水位数据,运行后形成稳定流,并利用模拟区内钻孔水位不断拟合校正,得到了该区校正后的相关水文地质参数:粉质粘土层的Kxx、Kyy、Kzz、给水度、降雨入渗系数分别为0.04 m/d、0.04 m/d、0.01 m/d、0.05、0.01;砂层的Kxx、Kyy、Kzz、给水度分别为5 m/d、5 m/d、0.8 m/d、0.21。
2.3 模型验证
为了验证地下水流模型的合理性和有效性,利用正演的方法进行检验。首先在稳定流的基础上,将南边水头边界赋为变化的河流时间序列水位值,并利用2015年8月—2016年1月的场地内CG-1钻孔的30组地下水位实测值与模拟值进行对比(图3)。可见观测孔的计算水位与实测水位的误差在1 m之内,整体变化趋势基本一致,表明最终选取的参数基本能代表整个含水层的水文地质特征。
3 溶质运移模型
3.1 控制方程和内部参数
污染物在地下水中的运移过程是对流、分子扩散和机械弥散综合作用的结果,分子扩散和机械弥散对溶质的迁移作用通常难以厘定,习惯上将它们统称为弥散作用[13],因此有以下溶质运移模拟的控制方程:

图3 CG-1孔模拟水位与实际水位对比图
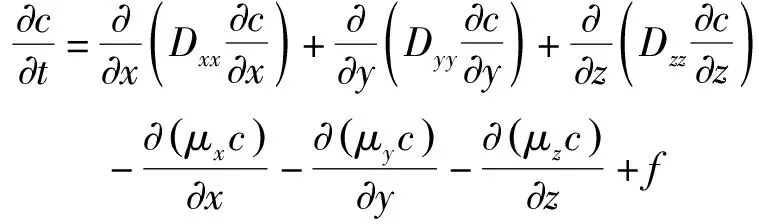
(1)
式中:等号右端前三项为弥散项,后三项为对流项,最后一项为由于化学反应或吸附解析所产生的溶质增量;Dxx、Dyy、Dzz分别为x、y、z三个主方向的弥散系数;μx,μy、μz分别为x、y、z方向的实际水流速度;c为溶质浓度。
在溶质运移方程中,弥散系数和有效孔隙度是两个重要的参数,弥散系数除了和含水介质本身性质有关,还依赖于地下水流速等因素,是个多指标变量,于是引入弥散度来反映溶质在地下水中的弥散能力,它和弥散系数之间的关系如下:
(2)
式中:Dd为有效分子扩散系数;δij为Kroneker数;|v|为流速向量v的模;αL、αT分别为纵向弥散度和横向弥散度;vi、vj为沿i、j方向的流速。在弥散度等参数的选取上,该模型的相关参数采用前人经验值:粉质粘土层与砂层的弥散度分别为0.006 m、0.5 m,有效孔隙度分别为0.08、0.2。
3.2 初始条件和边界条件
溶质运移模型的初始条件是描述地下水溶质浓度非稳定变化的初始状态,是后续模拟进行迭代计算的初始值,因此在赋值时必须加以明确,即使初始溶质浓度为零浓度。边界条件是模型内部和外界进行溶质交换的一种通道,它可以接受外界的溶质输入,也可以向外界输出溶质,因此边界条件是一个过程量,它伴随着模拟从开始到结束。在本模型中由于污染场地工厂已搬迁,除原有污染物外无其他污染物输入,因此假设污染场地均被污染,且浓度分布均匀。根据前期淋滤实验结果,以硝酸盐作为典型污染物,以淋滤实验获取的最大硝酸盐淋滤浓度400 mg/L作为初始条件输入,假设模拟区四周均无污染,并且假设地表水补给时不带来污染,因此边界条件不设置浓度边界。
4 模拟结果及分析
由于区内地下水主要为承压含水层,且其与地表江水联系十分密切,因此整个模拟针对承压含水层而言,即假设硝酸盐污染在承压含水层顶部,模拟其未来的变化情况。硝酸根离子易迁移,故整个模拟过程不考虑其被固相吸附[14]。本次模拟考虑两种情景:非稳定流和稳定流(流场见图4)。非稳定流符合地下水实际流场,地下水位随汉江水位的变化而变化;稳定流是假设的情景,其完全由江水补给地下水,南北水头值分别设置为22.9 m(汉江丰水期平均水位)和15 m。两种情景均设置了5个监测井用以了解研究区不同部位的污染物迁移分布情况(图4),两种情景的监测井位置完全相同,其中非稳定流井编号为1、2、3、4、5,稳定流编号为1’、2’、3’、4’、5’。1、2、3(1’、2’、3’)号井在场地内部,4(4’)号和5(5’)号在场地外部东北方向。模拟采用自动步长,设置总模拟时长为50年,并单独对第1、5、10、30和50年后的污染物浓度变化及分布进行讨论分析。
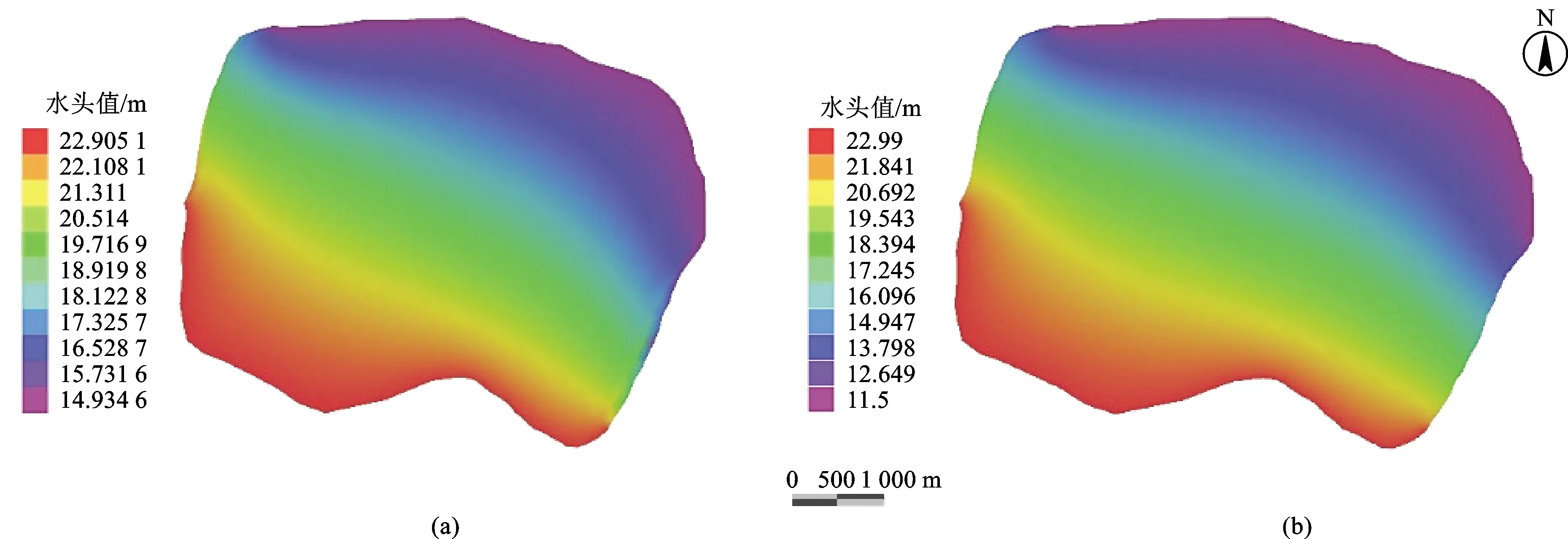
图4 稳定流流场(a)和非稳定流初始流场(b)
4.1 污染物平面分布
非稳定流模拟区污染晕的扩散方向整体呈北东向,和地下水流向基本一致(图5,图中为了更好地展现模拟效果,对模拟区进行了适当剪裁,裁剪范围见图1),同时污染物还存在向四周弥散的现象。在模拟时长为1年时,污染物有了一定距离的扩散,约为9 m,但扩散出的浓度并不大,为80 mg/L左右。在模拟5年之后,污染物向外扩散加快,污染场地的浓度在减小,场地西南处的浓度减小速度比场地东北处更快。在模拟期为10年、30年和50年时,污染物向场地东北方向扩散的距离在逐渐增大,分别为74 m、167 m和274 m,与此同时场地内部污染晕中心的污染物浓度和污染晕高值区面积在逐渐减小(图5-b)。模拟结束时承压含水层表面污染物的最大浓度为208.71 mg/L,与模拟初始时相比减小了约50%。
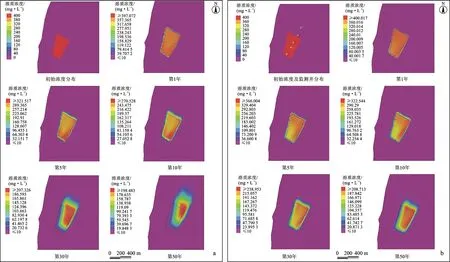
图5 稳定流与非稳定流溶质运移模拟结果对比
与非稳定流的溶质迁移模拟相比较,污染物在稳定流中的迁移速度和浓度减小速度更快,模拟1年的时间里便已经开始出现了较大扩散,扩散距离达到35 m;至50年模拟期结束时,污染物最大浓度为198.48 mg/L,最远扩散距离约为470 m(图5-a)。两种情景在不同模拟时间的最大扩散距离和浓度值见表1。

表1 不同模拟期的最大污染物浓度及扩散距离
非稳定流下几个监测井的模拟结果显示(图6-a),污染场地内部的井点浓度呈锯齿状逐年减小,其中1号井污染物浓度下降最快;2号和3号井下降速度大致相当,并且在50年时趋于平稳;4号井在模拟至2 700 d 时开始监测到污染物,且在10 000 d之前污染物浓度呈现上升的特点,之后增速极为缓慢,说明10 000 d 时污染晕的高值区经过了4号井,但是至模拟期结束,其污染物浓度到达了187 mg/L,且没有出现下降趋势,说明这段时间内污染物浓度高值区并没有完全迁移出4号井;5号井点由于距离污染场地较远,在模拟期内未检测出浓度。
稳定流的监测井污染物浓度曲线没有出现锯齿状变化,而是平滑地升高或降低。场地内的3个监测井同样出现下降,但是它们的下降速度比非稳定流更快,其中1’号井最为明显,且在11 000 d左右浓度已趋近于零,说明该厂区的污染范围整体上都进行了一定距离的迁移(图6-b);4’号井在模拟1 020 d时监测到了污染物,这一时间比非稳定流模拟提前了近1 700 d,稳定流模拟中4’号井的污染物浓度同样存在一个先快速上升后稳定的过程,但是在15 000 d时则开始缓慢下降,说明这一模拟污染晕浓度高值区已经迁移出4’号监测井;5’号井在9 000 d左右时也已监测到污染物,随后污染物浓度逐渐增大,至模拟期结束其浓度达到100 mg/L。

图6 监测井污染物浓度变化曲线
该模拟中若将初始的硝酸盐污染物看成是稳定示踪剂,以场地外的井点为污染物接收点,则污染物的迁移可简单处理为一个示踪过程,并由此产生穿透曲线。穿透曲线可以反映投放的示踪剂在含水介质中的迁移特征。本次模拟单独对4(4’)号井点的硝酸盐浓度曲线进行分析(图6-c),比较稳定流和非稳定流两种情况的溶质穿透过程。由于模拟年限和硝酸盐污染物初始量等原因,穿透曲线未能展示溶质浓度衰减的过程,从穿透曲线中得出了穿透时间等数据(表2)。可以看出,稳定流的溶质穿透时间更短,且其平均速度比非稳定流的最大迁移速度更大,说明稳定流具有更强的溶质运移能力,溶质容易在含水通道里扩散,而河岸潜流带中非稳定流对溶质的迁移起到了一定的阻滞作用。和稳定流相比,非稳定流的最大迁移速度和平均速度相差较小,这一现象也可以说明溶质在非稳定流中受到了地下水年际补排关系变化的影响。通过FEFLOW软件获取的地下水流速来看,地下水流速度比污染物迁移的平均速度小将近一个量级,表明地下水的渗透流速要远小于溶质的实际迁移速度,同时也反映了分子扩散在溶质迁移过程中发挥了较大作用。
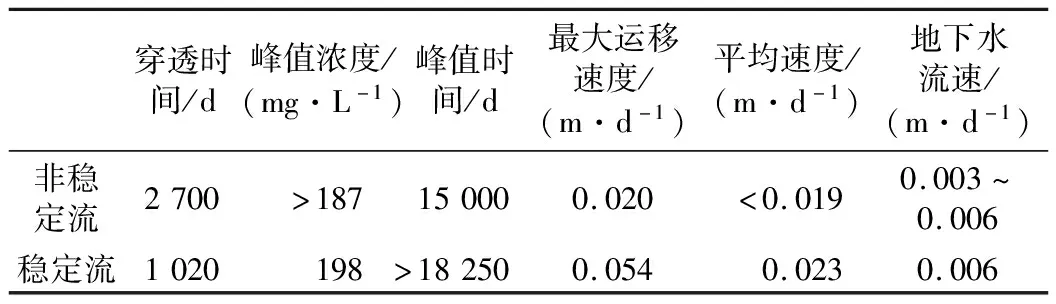
表2 稳定流和非稳定流条件下穿透曲线的相关参数对比
4.2 污染物垂向分布
为了解硝酸盐在场地垂向上的迁移过程,对5个不同模拟时间的硝酸盐浓度剖面图进行了分析(图7),剖面长度1.4 km,剖面方向30°(大致为地下水流方向),剖面线垂直穿过了整个污染场地。两种流场的污染物在模拟1年时间里基本到达了含水层底部,但其浓度较小,约为75 mg/L。随着模拟的进行,污染晕的浓度高值区逐渐向下移动,模拟期结束时,高浓度区均已运移至含水层底部。因此在垂向上,硝酸盐污染物的迁移总体表现为随着深度的增加,在模拟初期污染物浓度逐渐减小,而在模拟后期,浓度逐渐增大。模拟期结束时,非稳定流下污染物高浓度区的面积相对较大,说明在垂向上迁移也受到了地下水流的影响,即当污染物在水平方向运移受阻时,便会在垂向上有更多的聚积。因此在沿剖面方向上,非稳定流模拟的污染物扩散距离也小于稳定流情况下的扩散距离,比如模拟30年和50年时,非稳定流的污染物在含水层底部扩散最大距离分别为263 m和384 m,而稳定流情况下的扩散距离为462 m和745 m。
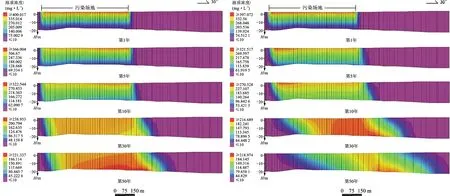
图7 不同模拟时间的污染物浓度剖面图(左:非稳定流;右:稳定流)
浓度剖面图(图7)显示随着深度的增加,污染物沿剖面方向的扩散距离增大,这一现象说明垂向上的溶质锋面往往最先受水动力影响,发生迁移,使得距离更大。此外也可能有地下水流速差异这一方面的原因,因为在河岸潜流带内,含水层底部的水头可能因为深部江水的高压强而增大,造成了含水层底部水流速度大,浅层流速小,这一解释在第10年、30年和50年的浓度剖面图可以很好地体现。当模拟至第10年时,污染物已经到达了含水层底部,且此时底部的扩散距离与浅层相比并不大,也就是说此时污染物失去了溶质锋面最先被迁移的优势,深部和浅层的污染物大致在“同一起跑线上”,但是在第30年和50年时,深部和浅层的扩散距离差明显加大。以非稳定流模拟情况为例,在第30年时,硝酸盐污染物在含水层顶部和底部的最大扩散距离分别为167 m和269 m,两者相差102 m;而在第50年时,底部和顶部的污染物最大扩散距离为123 m,比模拟30年时有所增大,表明溶质在垂向上的水平扩散很可能受到了地下水流速的影响。
5 结论
(1)河岸潜流带的承压含水层与汉江地表水存在着相互补给的关系,形成非稳定流。在平面上,非稳定流对潜流带的溶质迁移起到了一定的阻碍作用,比稳定流情况下的溶质更难迁移。模拟时间为50年时,污染物向东北方向的最大迁移距离为274 m,而相同时间下的稳定流模拟为470 m,溶质迁移主要受弥散作用的控制。
(2)在垂向上,污染物的迁移总体表现为随着深度的增加,在模拟初期浓度逐渐减小,而在模拟后期,污染物浓度逐渐增大。从剖面上来看,污染物在承压含水层底部的扩散距离比浅层远,一方面是溶质锋面最先被运移的结果,另一方面是含水层底部的地下水流速较大带来的流速差异而造成的。
(3)研究成果可为季节性河流或者水位波动较大的河流阶地地下水污染防控提供科学参考,研究地下水和地表水交互补给引起的潜流带内溶质运移的规律,可以更科学地阐释河流、湖泊潜流带中溶质的交换特征,为土壤和地下水修复提供科学依据。

