受洪水涨落影响的水位流量关系研究
程银才,张春霞
(1.山东农业大学 水利土木工程学院,山东 泰安 271018;2.泰安市水文局,山东 泰安 271000)
受洪水涨落影响的水位流量关系定线推流是水文资料整编的重要内容之一,整编方法有校正因素法、抵偿河长法、落差指数法和连时序法等[1-2],虽然方法较多,但这些方法多属于试算法,计算过程烦琐、效率低、精度不高,且计算成果因人而异,不适合计算机处理。
笔者在教学与科研中,有缘拜读了文献[3]和文献[4],收获颇多。 两文献总体结论正确,但存在些许瑕疵。 文献[3]存在两处瑕疵:①在“问题的提出”中,涨洪段和落洪段同水位两个实测流量与稳定流流量之差ΔQ和实测流量Q之比K很接近的假设不严谨,且缺乏足够理论依据;②在“关于假设ΔQ =KQ的证明”中,用ΔQ代替(H上为上断面水位)是错误的,进一步导致了ΔQ =KQ中(x为流量比重因数)的错误结论。 文献[4]存在两处瑕疵:①在“计算稳定流流量Q0的通式的推导”中,“设选定的入流断面(或河段长)不是任意的,而是特定的,即I -Q =Q -Q0(I为入流流量;Q为出流流量)”的假定无依据,概念不明确,且将该假定直接用于后文的证明中;②推导出的结论有误。
笔者对受洪水涨落影响的不稳定流的流量与同水位稳定流的流量之间的关系进行了研究,并推导出受洪水涨落影响同水位稳定流流量与不稳定流流量之间的关系式,从新的角度证明了ΔQ与Q具有函数关系。
1 ΔQ 与Q 函数关系的证明

线性马斯京根法由水量平衡方程和槽蓄方程[5]组成:式中:W为河段的槽蓄量;I和Q分别为上断面入流流量和下断面出流流量;k为蓄量常数;x为流量比重因数。
稳定流条件下,有

式中:W0为稳定流时槽蓄量;Q0为稳定流时下断面出流流量。
如图1(a)所示,在t时刻,河段水流为稳定流,附加比降ds =0。 假设河段水面呈直线[6],水面线如①线所示,此时,I =Q =Q0。 此后,洪水来临,河段处于涨水阶段(见图1(b)),ds >0,在t +dt时刻水面线如②线所示。 图1(c)表示在t +dt时刻河段处于落水阶段,ds <0,水面线如③线所示。 图1 中,从t到t +dt时段内,下断面水位恒定不变,为z2。

图1 受洪水涨落影响的水面线
图2 中,河段长为一个特征河长l。 在t时刻,水流为稳定流,水面线如①线所示。t +dt时刻河段处于涨水阶段,水面线如②线所示。 从t到t +dt时刻,上断面至中断面槽蓄量增量dW >0,可用式(1)计算:


图2 特征河长下受洪水涨落影响的水面线
比较图2 的t与t +dt两个时刻水面线,根据特征河长的含义[6],对于下断面,水位降低导致的流量减小与比降增大导致的流量增大正好抵消,使得下断面流量不变(仍为t时刻稳定流流量Q0)。 中断面至下断面槽蓄量增量dW <0,可用式(1)计算:
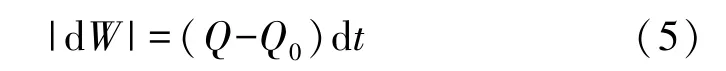
由式(4)和式(5)得:

另由式(2)可得:

将式(6)代入式(7),整理后得:

根据水力学原理,断面流量是水位z和水面比降s的函数,则由I =I(z1,s) 得


又Q =Q(z2,s) ,考虑到z2恒定,则

由水力学中曼宁公式Q =R s(R为流量模数)得

将式(10)~式(12)一并代入式(7),整理后有
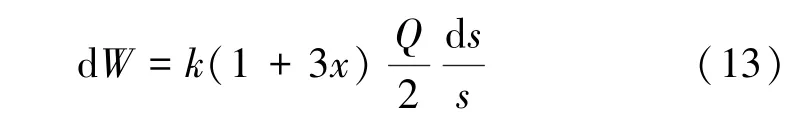
受洪水涨落影响的水位流量关系为

式中:Q和Q0分别为同水位不稳定流与稳定流的流量;s0=s -ds,为稳定流的比降。
一般情况下,ds≪s0,则由式(14)有

将s0=s -ds代入式(15)可得又dQ =Q - Q0,则

将式(16)代入式(13),有

比较式(8)与式(17),有1+x =(1+3x)×,据此整理得

式(18)即是同水位不稳定流流量与稳定流流量之差和不稳定流流量之间的微分式,相应的差分式为。
2 受洪水涨落影响的同水位稳定流流量与不稳定流流量之间的关系
根据受洪水涨落影响的水位流量关系的原理式(15),有

由(19)式得

整理上式,有

任取某一水位z(见图3),与其对应的稳定流流量为Q0,与z对应的不稳定流在涨、落水时流量分别为Q1和Q2,与z对应的涨、落水时水面比降分别为s1与s2。

图3 受洪水涨落影响的水位流量关系
因Q0和s0只随z变化,则由式(14)可得:

由式(21)可得:

由式(23)可得:


式(25)即为受洪水涨落影响的同水位稳定流流量与两个不稳定流流量之间的关系式。
3 ΔQ 与Q 具有函数关系的再证明

定义ΔQ为受洪水涨落影响的同水位稳定流流量和不稳定流流量之差(且恒取正值,目的是使得K >0),即ΔQ =|Q - Q0|,因Q1>Q0,Q2<Q0,结合式(26),可得:

式(27)即是从新的角度对ΔQ与Q具有函数关系的再证明,其较文献[3]的证明过程更简洁,原理更清晰。
4 结语
(1)受洪水涨落影响的同水位不稳定流流量与稳定流流量之差和不稳定流流量之间的关系应为ΔQ =,文献[3]和文献[4]的相关结论有误。
(3)受洪水涨落影响的同水位稳定流流量与两个不稳定流流量之间的关系为,该结论与实际河段是否恰好是一个特征河长无关,因此可用于任意河长的河段。

