关注儿童数学现实,开展结构化教学——以“认识底和高”一课为例

◇汤其鸣

每个学生都有自己特定的观察、思考以及反映这个世界各种数学概念、运算方法、规律和有关数学知识结构的方法。数学教育要紧贴着儿童已有的数学现实，站在整体化、系统化的高度下展开结构化教学，帮助儿童将自己已有的数学现实与当下的数学学习产生联结，以促进儿童的数学学习不断进步，继而形成新的数学现实。下面以北师大版教材五年级上册“认识底和高”一课为例，谈谈关注儿童数学现实下进行结构化教学的几点做法。

一 凸显本质，明晰原点

在儿童已有的数学现实里，学的许多知识是游离的，呈点状或块状，且由于受到“生活数学”的干扰，更易引起儿童对数学本质的把握不到位。例如“高”这一名称对于学生来说并不陌生，如身高等。大多数教师在教学本课后发现，有一部分学生总是把高画错。根据对学生的访谈与教学实践得知：虽然学生对高的认识最熟悉的是测量身高，但由于实际中他们很少自己动手测量，所以对于高的界定是模糊的，知道身高是可以测量的，但不能与已学的线段产生联结，对于“高是一条线段”的本质也就不明晰。剥离干扰因素，引导学生认清知识本质，找到学习的原点，这一点是至关重要的。在这个过程中，可引导儿童将新知纳入已有的认知结构，有利于儿童快速地同化新知，使知识产生更为丰富的内涵。

教学片段一

师：同学们听说过高吗？

生：听说过。

师：（出示人、树、房图片）在这些物体中都有什么高呢？谁上来指一指身高、树高、房高分别在哪儿？注意观察他的动作。

（一生上台指高）

师：通过他刚才的动作，你感觉高是什么？

生：是一条线。

生：是一条线段。

师：哪种表达更合适？为什么？

（生答略）

师：既然大家都同意高是一条线段，你能说说线段有什么突出的特征吗？

生：有两个端点。

师：高这条线段的两端应该分别在哪儿？

（生结合图片指出：人的头顶和脚底，树顶和树底……）

认识顶点和底这两个名称，同时知道“高”这条线段所在的范围，即在顶点与底之间。

学生所学到的数学知识不是老师课上教的结果，而应当是学生通过对现实生活的观察思考发掘出来的结论。因此，高既然对于学生来说并不陌生，那么应当从生活中来再到生活中去。从学生粗浅的认识出发，逐步还原“高”的本质，明白这样的一条线段在图形中与底互相垂直时有了个新名称叫作“高”。把新概念纳入旧结构中，同时为后面画高时能准确地找到高所在的区间与位置做了良好的铺垫，增强了知识结构的稳固性。

二 迁移整合，完善认知

认知心理学家认为，迁移是学习中普遍的现象，是检验我们在教学中是否培养了能力、发展了智力一个比较可靠的指标。只有创造适合的或相似的活动情境，再现他们已有的数学现实，才能较好地实现迁移。

教学片段二

师：认识了底和高，现在请同学们动手画一画这个三角形的高，并测量出它的长度。

（生画、量）

师：大家都迅速地完成了测量，只是老师很好奇，这么一条线段，你们是如何画出来的？

（生示范画高）

师：（诧异）大家为什么这么熟练？

（生回忆，与之前画垂线段的方法是一样的）

教师演示：隐去三角形的两边。从视觉直观沟通新旧名称之间存在的关系，完成直线外一点与顶点等的迁移，把画高技能与画垂线段技能整合起来。

不可否认的是，在学习中会有一些负迁移干扰儿童的认知，这些负迁移往往来自儿童的“生活数学”经验，如生活中我们认识的高都是一条与地面垂直的线段，这是由于受地球引力的影响，而今天这节课中研究的是图形中的高，与之是有“矛盾”的，如何整合，完善学生对高的认识？

教学片段三

师：有个小朋友画出了这个三角形的高，（如图1）他和大家画的怎么不一样？这是怎么回事？这条线段是这个三角形的高吗？

（生争论，表达看法）

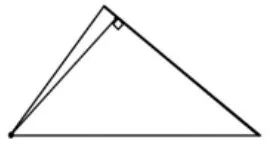
图1

释放学生的疑惑，与生活中所见的“高的样子”产生冲突，最后形成共识：图形是可以旋转的，所以当三角形旋转后，每条边都是它的底，每条底上对应着一条高。

结构化教学从某种角度看，是使知识的内涵更为丰富与完善的过程，教师通过巧妙的活动和讨论来揭示儿童的误解和顽固的表现性错误，有利于儿童间互相促进与调整，跳出认识误区，重新建立正确的认识。

三 求同存异，融通结构

要用发展的眼光看待不变的事物。在数学学习中，我们应鼓励学生用动态的眼光来看待静止的知识。特别是在图形与几何领域的知识中，通过图形的运动探索并确认图形的一些性质，有助于发展学生的几何直观能力和空间观念。儿童受具象思维的影响，大部分的发现与思考需要依赖直观的操作，利用几何图形的直观性，可以让儿童充分地动手操作，研究静态知识背后的动态发展。

教学片段四

师：老师给同学们带来了一个会动的三角形（三粒磁扣，一条封闭橡皮绳）。想想看，怎么动，高的长度仍旧可以保持不变？

（生上台把三角形的底在底所在的直线上平移拉伸）

师：为什么平移底，高的长度不变？

生：底与顶点之间的距离保持不变。

师：除了平移底，还有其他方法也可以使高的长度保持不变吗？

（生尝试平移顶点）

师：说说看，顶点怎么动，高的长度不变？

生：与底保持平行。

（师课件出示图2）

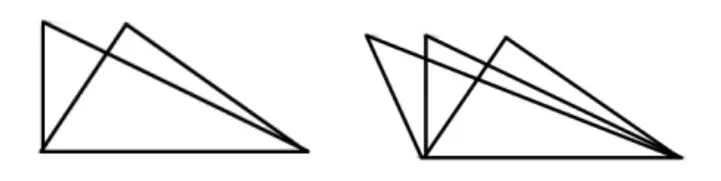
图2

师：在平行线间移动底或顶点，高的长度不变，也就是平行线间距离处处相等。

师：现在你能解释生活中人们为什么用这样的方法测量身高吗？（如图3）

（生答略）

图3

师：观察这几个我们刚刚移动顶点产生的三角形（如图4），它们的高相等吗？

图4

生：相等。

师：你还有什么发现？

生：高可以在图形内，高可以在图形上，高也可以在图形外。

钝角三角形高的认识一直是儿童学习上的难点，它的画法不要求学生掌握，但有必要认识它的存在，这是高的内涵完整性的体现。在“如何让高保持不变”的动态探究中，把顶点变成一条线，让学生以一组平行线的视角来看高的范围，解释生活中的现象，为后面研究梯形与平行四边形的高打开思考，同时把各类三角形高所在的位置完整呈现，在“同”中研究“异”，使学生新建立的高的认识又向前进了一步。