水库水量平衡计算中消除水位跳变影响的过滤算法

(南瑞集团 国网电力科学研究院，江苏 南京 211000)

水库调度是水电站工程管理的主要环节之一[1-2]。目前我国大中型水电站均已建立起水库调度自动化系统[2]，同时，大规模流域梯级电站开发使得各水库水力关系更为复杂[3]，流域梯级水电协调优化调度对入库流量数据质量及来水预测精度提出了更高的要求。水电站防汛、生产和参与市场运行也对流域水情信息共享、数据质量提出新的迫切需求。

在水情水调自动化系统中，入库流量是最为重要的水情数据，入库流量计算的准确度直接影响调度决策。目前常用的入库流量计算方法有水量平衡法、区间推流法、入库控制站代表法等，其中以水量平衡法应用最广。该算法基于水量平衡原理，用时段内入库水量减去出库水量得到库内水量变化值，利用库容变化和出库流量反推计算入库流量[4]。但该算法对坝上水位数据的敏感度较高，特别是水库面积较大时，坝上水位的小幅波动会导致库容差大幅跳变，从而影响入库流量计算，使入库流量呈现锯齿状震荡，无法准确反映实际情况。

为解决入库流量计算异常问题，许多水调系统均对其进行处理，如水位变幅限制、多水位站平均、入库流量滑动平均、动库容算法等，但各有优劣和适用条件。

近年来，雷达水位计在水情测报系统中得到广泛应用[5-7]，其易安装、高精度(可达mm级)、非接触式的测量方式深受用户喜爱。但雷达水位计也存在弱点，如易受内外环境影响，出现偶发性小幅跳变(主要为测值向下跳变)，导致入库流量计算不准。该问题不易从硬件设备上根除，因此需要对水位跳变进行过滤处理。

鉴于此，本文在对水量平衡算法中水位变幅对入库流量计算结果的影响进行深入分析的基础上，设计了一种基于水量平衡模型的库水位跳变过滤算法，以最新水位来数、时间、系统中已有的前一次水位、时间为实时参数，利用水位库容曲线计算库容差流量，并以水位最大出库流量反推库容差流量的合理性，以此对最新水位来数进行过滤分析和处理。实践表明，该算法能有效过滤因水位计读数跳变(变小)导致的库水位跳变问题，使入库流量计算更为准确。

1 入库流量水量平衡算法

1.1 算法介绍

水量平衡是水文学基本原理之一[8]，也是水调系统中最常用的流量计算方法。该算法利用机组出力、坝上坝下水位、闸门开度等信息，通过机组NHQ曲线、闸门泄流曲线、水库水位库容曲线等特征曲线插值计算，得到小时、日的发电量以及泄洪、出库、入库流量。

算法流程如下：

(1) 获取计算时段坝上坝下水位、机组出力、闸门开度；

(2) 调用机组NHQ曲线(机组出力-水头-过机流量三维曲线)、闸门泄流曲线(库水位-闸门开度-过闸流量三维曲线)、水位库容曲线(库水位-库容二维曲线)；

(3) 根据坝上坝下小时平均水位差值计算小时平均水头；利用水头和机组出力，三维插值NHQ曲线，得到机组过机流量，各机组过机流量相加即得到全厂发电流量；

(4) 根据坝上水位以及闸门开度三维插值闸门泄流曲线，得到闸门泄流流量；

(5) 将发电流量和泄洪流量相加得到出库流量；

(6) 利用时段初、末库水位二维插值水位库容曲线得到时段初、末库容，两者相减得时段库容差，除以时间得库容差流量(虚拟流量)；

(7) 利用水量平衡原理，用时段入库水量减去库容差得出时段出库水量，再将出库流量和库容差流量相加，即得入库流量。

算法流程如图1所示。

1.2 算法特点及常用处理方法

入库流量水量平衡算法原理简单，计算所需原始数据易获取，因此在各水调自动化系统广泛应用。

但由于其算法中库容差流量的计算对坝上水位变幅较为敏感，对水库面积较大的水库尤为明显，如丹江口水库、新安江水库、龙羊峡水库等，坝上水位的小幅波动会导致库容差流量大幅跳变，从而影响入库流量计算结果[9-10]，若不加以处理，入库流量值将出现大幅震荡，甚至出现入库流量为负的情况。

为解决此问题，许多水调系统采用了不同的处理方法，常用方法有：

(1) 对水位变幅进行限制，将超限制的水位抛弃，这会导致数据缺失，且变幅判别阈值是人为设定的某一固定值，无法根据实际运行情况自动调整，因此该方法仅限于对大幅异常跳变进行处理。

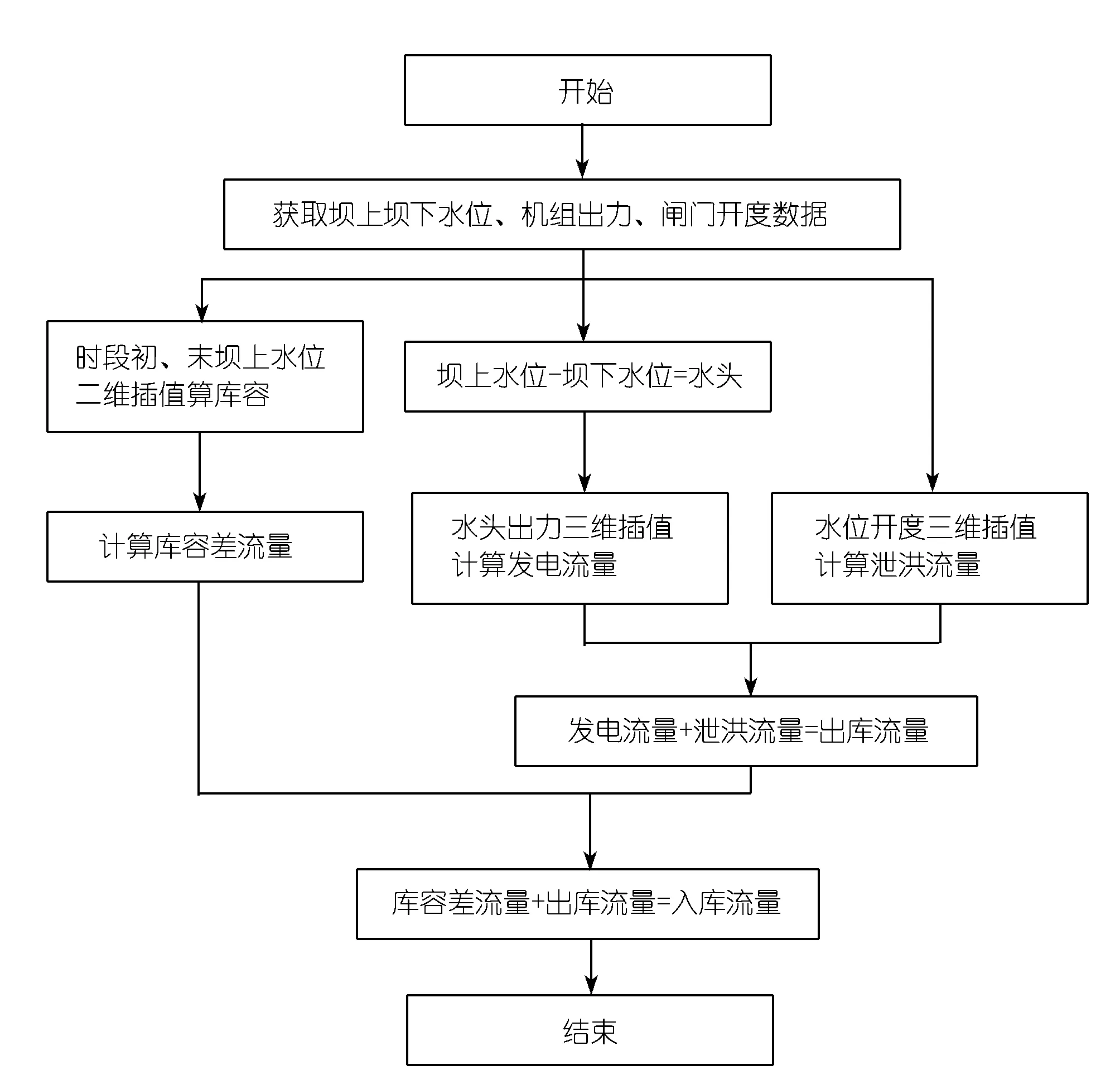
图1 水量平衡算法流程Fig.1 Flow chart of water balance algorithm

(2) 在水库不同位置设置若干个代表站，求平均库水位计算入库流量，降低单一水位对入库流量计算的灵敏度，减小误差影响，但仍无法排除跳变影响，且多水位站建设成本较高。

(3) 采用滑动平均算法计算入库流量，将一小时入库流量计算变为若干小时平均入库流量计算，从而得平滑波动值[11-12]。但该方法具有一定局限性，入库流量数据不灵敏，无法分析短时峰谷流量，特别是山区水库，其入库流量具有陡涨陡落特性，因此不适用于滑动平均算法。

(4) 少量大型水库如三峡水库采用动库容方式计算入库流量[13-15]，该方法计算入库流量较为准确，但需设置多个水位站并有完整水库(河道)断面资料支撑，仅适用于入库流量较大的狭长型水库。

2 水位跳变对流量计算影响分析

针对库水位跳变对入库流量计算结果的影响，以槟榔江三岔河水库水情水调系统为例，进行定量分析。

槟榔江三岔河水库水情水调系统坝上水位采用高精度(mm级)雷达水位计监测，其测值会出现偶发性小幅跳变(变小)。2018年8月2日出现坝上水位数据小幅跳变情况，30 min水位测值下降0.090 m。系统虽已设置1 h水位变幅超过0.2 m即变幅报警，但仍无法对上述小幅跳变有效判别。若不加以处理，根据水量平衡算法计算得到的入库流量将出现较大波动。水位过程线和入库流量过程线如图2所示。

由图2可见，0.090 m的坝上水位跳变，即可导致±290 m3/s的入库流量误差，其敏感度可见一斑。

若采用常规变幅判别阈值进行限制，则需将阈值设定为小于0.1 m。但由于水库水位库容曲线斜率不一致，在水位较高时，单位高差库容较大，水位较低时，单位高差库容较小，如果变幅阈值设定过小，则在低水位时可能引起误判。

水位库容曲线如图3所示。

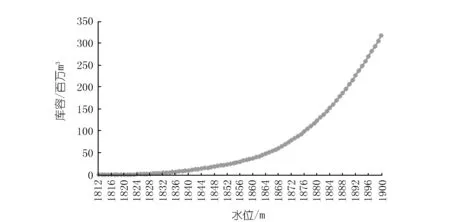
图3 三岔河水库水位库容曲线Fig.3 Storage-capacity curve of Sanchahe Reservoir

由图3可知，在水位为1 893 m时，0.1 m水位变幅将产生100万m3的库容差；而在水位为1 860 m时，0.1 m水位变幅仅产生20万m3的库容差，两者相差5倍。在高水位时，变幅超过0.1 m即为异常，而低水位时，正常变幅即可超过0.1 m。

水位库容曲线为水位面积曲线积分所得，在水量平衡算法中，库容差即为当前水位下水库面积乘以水位差。因此，相同计算时段和水位变幅下，水库面积大小与流量值大小比例一致，两者呈线性正比关系。

此外，不同水位下，水库泄水能力也有所不同，可根据水位-最大过机流量曲线和水位-闸门全开曲线插值得到。

综上，为避免误判，实际应用中一般仅设置较大的水位变幅阈值，过滤极端跳变情况，难以对小幅度水位跳变进行有效处理。

因此，需寻求一种可根据水位高低及水库库容特性(水位库容曲线或水库面积曲线)、水库泄水能力自动计算判别阈值的算法，实现不同水位下库水位合理变动幅度自适应计算，从而提高异常跳变过滤的精准度，同时避免误判。

3 水量平衡反推库水位跳变过滤算法

3.1 算法介绍

槟榔江三岔河水情水调系统中，以水量平衡模型反推库水位，利用不同水位下最大出库流量限制其合理变幅，以此过滤异常跳变。

(1) 系统新水位数据插入时，首先根据数据标志位判别是否为人工录入(校核)，若是人工录入，则不作处理，直接写库；若是遥测站自动上报数据，则查找系统中已存库最近一次水位和时间，并计算两者之间的时间差ΔT。

(2) 利用两个水位二维插值水位库容曲线得到对应库容，并计算库容差ΔV；

(3) 根据水量平衡，由ΔV/ΔT得到库容差出库流量(出库流量-入库流量)，假设最小入库流量为0，则此值即为最小库容差出库流量QKmin；

(4) 利用水位插值溢洪道全开泄流曲线得到该水位下的最大泄洪流量QXmax；利用水位插值机组最大出力过机流量曲线得到最大发电流量QFmax(尾水位基本固定，对水头影响忽略不计)，两者相加得到该水位下的最大理论出库流量QLmax；

(5) 比较QKmin和QLmax的大小，若QKmin>QLmax，则说明本次水位变动下，最小库容差出库流量大于最大理论出库流量，判定本次水位属于异常跳变(变小)，更新本次水位值为最近一次水位值，并发出异常告警。

算法流程如图4所示。

3.2 算法特点

(1) 该算法对水位变幅的判定基于水量平衡模型，根据实时水位和水库泄洪能力、发电机过流能力，反推最大库容差流量，进而判断新插入水位值是否异常。因此单位时间变幅阈值随水位的变化而不同，库水位高时，水库面积较大，同样的水位差对应的库容差更大，允许的变幅更小；库水位低时，水库面积较小，同样的水位差对应的库容差更小，允许的变幅更大。这比单纯的人工设定某一固定变幅阈值更为精确合理。

(2) 出库流量采用最大泄流流量和最大发电流量计算而不采用实际闸门开度和机组出力计算，是基于系统健壮性考虑。在水情系统中一般水位数据较机组出力和闸门开度数据更易获取，若水位数据异常判断需实时机组和闸门数据作为计算基础，则算法稍显复杂，且一旦出现机组闸门数据中断，轻则算法无法正常计算，重则出现误判，导致系统紊乱。

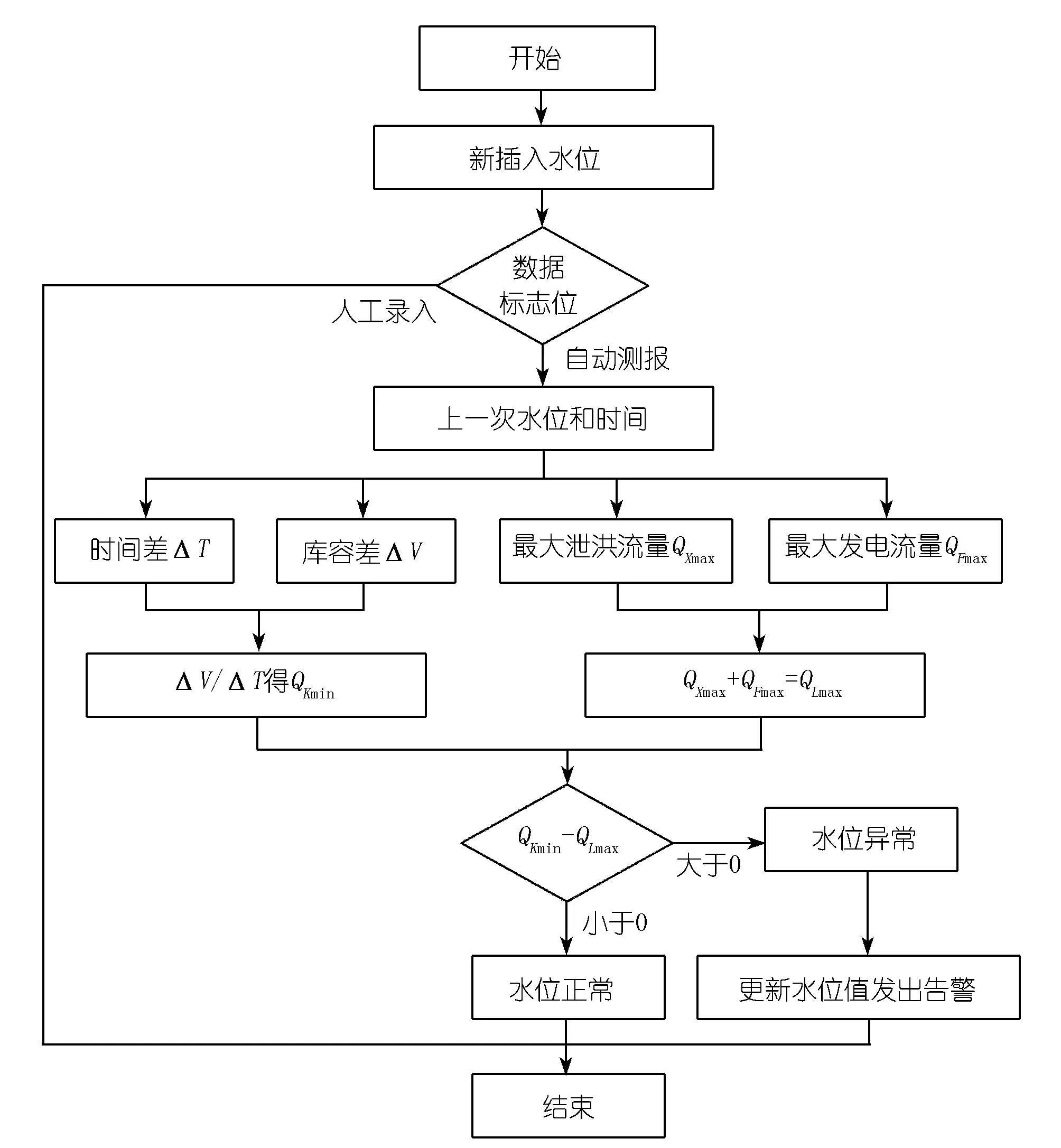
图4 水位跳变过滤算法流程Fig.4 Flow chart of water level fluctuation filtering algorithm

(3) 当判定某次水位测量值为异常跳变时，算法修改本次水位值为系统中已有的前一次水位。该处理方式基于以下3方面考虑：① 若直接抛弃异常数据而不置数，则将导致数据缺失，影响流量计算；② 根据实际运行情况，水库水位测量时间间隔较短(1 h以内)、库水位升降速率较慢，因此相邻时段水位可做适当延展(可根据前一次水位定值延展，也可根据前两次水位变化情况同斜率延展)；③ 判定异常跳变后系统发出告警信息，提示值班人员核实，若算法延展的水位数据确有不妥，还可人工修正。

(4) 本算法利用水情水调系统数据库触发器实现，无需额外运行程序，算法稳定，响应迅速，便于系统现场实施以及推广应用。

(5) 为便于用户察觉水位计跳变问题，本算法将处理情况发送给报警系统，同时将本条数据置于特殊标志位，在系统中以不同颜色展示，使用户能及时知晓数据过滤情况，以便及时对高故障率水位计进行维护更换。

4 实例应用

将本算法应用于槟榔江三岔河水情系统，对前文描述的8月2日水位跳变进行过滤处理。新插入水位为1 893.201 m，时间为2日1：00，系统中前一次水位为1 893.291 m，时间为2日0:30，两者时间差为30 min，根据库容曲线，对应库容分别为239.85×106m3和238.99×106m3，库容差出库流量达478.0 m3/s。而此水位下最大溢洪流量为386.0 m3/s，最大发电流量为47.7 m3/s，最大理论出库流量为434.0 m3/s，小于库容差出库流量478.0 m3/s。因此，判定本次插入的水位属于异常跳变，修改本次水位值为系统中已有的前一次水位1 893.291 m。

过滤后，新的坝上水位过程线以及重新计算后的入库流量过程线如图5所示。

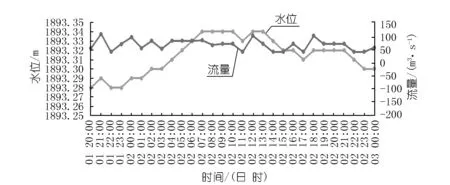
图5 过滤后水位-入库流量过程线Fig.5 Graph of water level-reservoir inflow after filter

与图2中未过滤水位-入库流量过程线比较，其入库流量震荡明显减弱，更为合理。事实上，过滤后水量平衡算法入库流量为53.5 m3/s，利用三岔河上游大岔河、胆扎河、拉拉河、轮马河4个入库流量站实时流量加库区区间流量比例求和得到的推流入库流量值为58.6 m3/s，两者比较接近。

5 结 语

本文将水量平衡模型引入库水位跳变过滤算法中，利用水位库容曲线、机组最大过流曲线和闸门最大溢洪曲线插值计算当前水位理论最大出库流量和库容差流量，当库容差流量大于理论最大出库流量时，判定本次水位数据属于异常跳变(变小)，对其进行过滤和处理。实例计算表明，本算法能根据不同水位情况自动调整变幅判断阈值，从而准确有效地过滤水位小幅跳变(变小)异常，且避免误判。

本算法实现方式简便、响应迅速、运行可靠，对系统其他数据依赖度低，适用于使用雷达水位计作为坝上水位自动监测设备的水库和电站，可用于新水情水调系统设计开发，也可针对已建系统进行优化完善，具有较好的推广应用价值。

同时，由于本算法仅对水位向下跳变进行分析过滤，针对水位上涨跳变问题，虽可通过上游入库流量站实时流量作为判据反推计算，但增加算法对其他遥测数据的依赖，稳定性无法得到保障。因此，水位上涨跳变问题尚需与其他方式(如定值判断、人工处理等)协同处理解决。