南水北调中线干线节制闸过流公式率定及曲线绘制

李 景 刚，乔 雨，陈 晓 楠，黄 诗 峰2，高 林

(1.南水北调中线干线工程建设管理局，北京 100038； 2.中国水利水电科学研究院，北京 100038)

南水北调中线干线全程1 432 km，自汉江丹江口水库引水，穿越长江、淮河、黄河、海河4个流域，沿途分别向河南省、河北省、天津市、北京市供水，是缓解我国华北地区水资源短缺、实现我国水资源整体优化配置、改善生态环境的重大战略性基础设施工程。工程沿线共布设了 97 座分水口门和 64 座节制闸，无在线调蓄水库，需通过各闸门的联合调度实现按用水计划平稳输水的目标[1-3]。其中，节制闸均为弧形闸门[4-6]。南水北调中线干线工程于2014年12月12日正式通水，当前正处于初期运行阶段，按照SL75-2014《水闸技术管理规定》[7]等规范要求，需逐步建立健全各类闸门技术档案，尤其是闸门过流能力率定和闸门控制运用图表绘制等，这对于精确实施渠道控制、指导闸门日常控制操作、保障输水调度安全具有重要意义[8-9]。

目前，闸门过流计算方法概括起来主要有传统水力学法和量纲分析法两类。其中，传统水力学法主要是基于能量方程进行过流公式推导，求解流量系数和淹没系数等关键参数，并在此基础上结合工程实际，进行经验公式改进和修正[6，9-12]。而量纲分析法主要是通过量纲分析来构建闸门流量与开度、上下游水深之间的表征关系式,最早由Ferro Vito提出[13]。对于上述两种过流计算方法，穆祥鹏等分别采用Buyalski弧形闸门模型试验数据和南水北调中线京石段部分节制闸现场观测数据进行了计算分析比较，结果显示：传统水力学法中的有关过流参数，因多由根据试验或原型数据获得的经验公式或图表进行求取，易产生较大的误差[9]；同时因为闸门的水力关系复杂，率定工作通常难度较大。而量纲分析法其物理概念比较清晰，公式形式较为简单，在有闸门实测数据的条件下能够获得较高的计算精度，易于率定，是进行闸门水力计算的较好选择。

本文基于量纲分析法，以刁河节制闸为例，利用南水北调中线干线通水运行观测数据，在孔流条件下开展节制闸过流公式率定，并在此基础上绘制节制闸不同闸前、闸后水位差下的过闸流量与闸门开度关系曲线，以指导调度人员掌握闸门运行状况、适时开展闸门日常调度。

1 量纲分析法

对于弧形闸门，假定在淹没流情况下，单宽流量q是闸门开度e、重力加速度g、能量差He和绝对黏性系数μ的函数，其函数关系可用式(1)表示，其中，能量差He可由式(2)得到[14-16]。

q=f(e,g,He,μ)

(1)

He=H0-Ht

(2)

假定过闸流量具有如下形式：

(3)

式中,a,b,c,d和m为常数系数。

利用量纲分析可得：

(4)

式(4)左边表示矩形渠道的临界水深，若用K表示，则有

(5)

式中，K=(q2/g)1/3,q是闸门的单宽流量；e是闸门的开度；He是闸门的上下游水位差；i和j分别是与闸门型式和过闸流量有关的经验系数。

对于自由流状况，上式依然成立，只是将下游水深Ht设为0。

对于南水北调中线干线节制闸，单宽流量为

(6)

式中，Q是节制闸的总输水流量，N是参与运行节制闸的孔数，B是节制闸闸门宽度。

而对于公式(5)，当两边同时取对数时，有

(7)

可知，在对数坐标系中，节制闸无量纲过闸流量计算公式是一个线性方程，对于流量系数i和j可根据最小二乘法计算确定，即

(8)

进而得到节制闸过闸流量为

(9)

2 节制闸过流公式率定

本文以南水北调中线干线刁河节制闸为例，利用正式通水以来的水情观测数据合理选取样本点进行过闸流量公式参数率定。样本点选取具体原则如下。

(1) 数据观测前24 h内闸门开度未作调整，保证过闸流量的相对稳定。

(2) 流量变化区间要尽量拉开，且取点分布尽量均匀。

(3) 孔流分界点按e/H0<0.65控制[17]，其中H0为上游观测水头。

按照上述原则，本文共选取刁河节制闸2014年12月至2018年5月间闸前、闸后水位、闸门开度及过闸流量观测数据共40组，见表1。

表1 刁河节制闸水情数据Tab.1 Water information of the Diaohe check gate

依据公式(8)，通过线性拟合得到刁河节制闸过闸流量率定曲线如图1所示，其决定系数超过了0.99。进而，得到该节制闸流量系数i=100.0567=1.139 5，j=0.261 9。

另外，刁河节制闸为2孔闸门，单闸宽度为13 m，最终求得刁河节制闸孔流条件下的过闸流量曲线关系为

(10)

3 精度分析

由图1可以看出，由观测样本数据率定的刁河节制闸过闸流量曲线呈现出显著的线性关系，说明观测样本选择整体合理。因此，采用无量纲流量计算公式不仅能简化流量系数的率定过程(只有两个未知数)，同时也有助于剔除不合理的观测数据，从而提高流量系数的率定精度。

图1 刁河节制闸过流公式率定曲线Fig.1 Calibration curve of flow equation for the Diaohe check gate

另外，本文采用误差分析法对流量率定曲线计算所得的刁河过闸流量精度进行计算分析。其中，平均误差按照下式计算[2]：

(11)

式中,E为计算的平均误差；q为实测流量值；q′为计算流量值；n为样本的数量。

根据表1中数据，利用本文构建的刁河节制闸过闸流量曲线公式(10)计算出流量相对误差基本都在±6%以内，而平均误差为2.46%。为进一步检验本文构建的节制闸过流公式其率定精度，另选取11组观测数据进行检验，见表2。从检验结果来看，实测流量与计算流量误差均在±5%之间，而平均误差为2.81%，计算精度相对较高。同时，随着南水北调中线干线工程的持续运行和水情观测数据的不断丰富，通过对观测样本数据的深入优化筛选[18]，节制闸过流公式率定精度还将会得到进一步地提升。

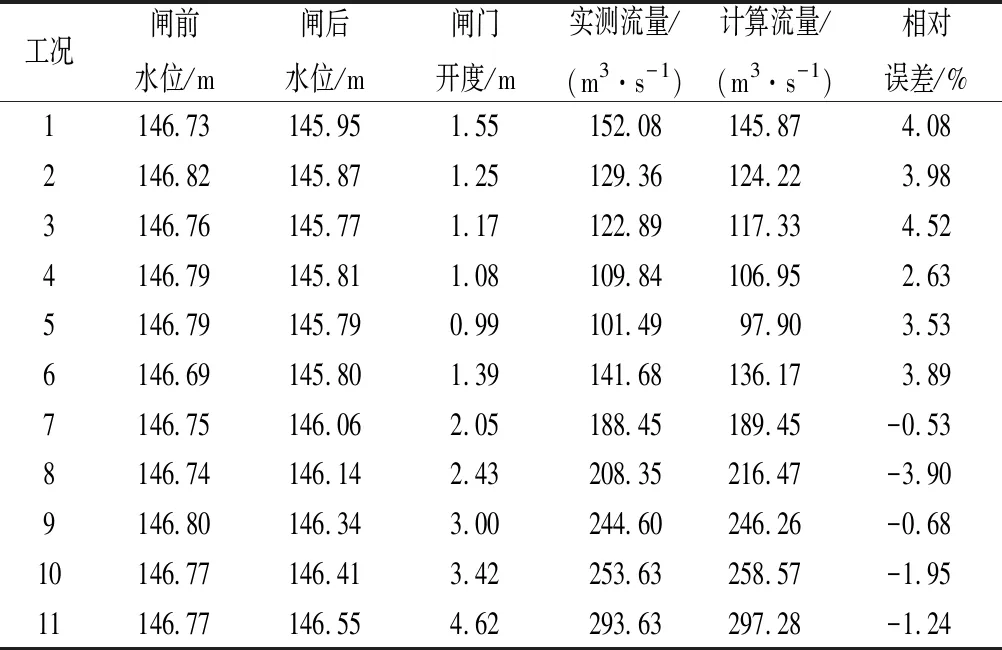
表2 刁河节制闸过流公式率定精度检验Tab.2 Accuracy test of calibrated flow equation for the Diaohe check gate

4 节制闸过流曲线绘制

对于式(10)，当He为常数项时，演变为一个以闸门开度e为自变量、过闸流量Q为因变量的幂函数。设He=0.2 m时，可计算得到当闸门开度e=1,2,3,4,5时所对应的Q值，这样就得到了一条He=0.2 m时的开度-流量(e～Q)关系曲线。重复上述步骤，可依次得到He=0.4,0.6,0.8,…,1.2 m时的一系列开度-流量(e～Q)关系曲线(见图2)。

在调度运行过程中，当节制闸过闸流量需进行调整时，根据闸前、闸后水位通过曲线可以确定闸门开度，为闸门调度人员设定闸门开度值提供依据；另外，调度人员可以根据闸门开度和闸前、闸后水位查询相应的过闸流量，从而掌握过闸流量的变化，适时开展闸门调度，保障全线输水调度安全[8]。

图2 刁河节制闸开度-流量关系曲线Fig.2 The e-Q relation curve of the Diaohe check gate

5 结论与讨论

本文以刁河节制闸为例，基于量纲分析法，在孔流条件下利用南水北调中线干线通水运行观测数据开展了节制闸过流公式率定，并在此基础上绘制了节制闸不同闸前、闸后水位差下的过闸流量与闸门开度关系曲线。结果显示：基于量纲分析法物理概念比较清晰，公式形式较为简单，只包含两个常数系数，因此率定工作量较传统水力学法大大降低；同时，在有实测水情数据的条件下，率定后量纲分析公式能够达到很好的计算精度，是进行闸门水力学计算和实现自动化调度的很好选择；另外，节制闸过闸流量曲线的绘制，为日常调度人员掌握过闸流量变化、适时开展闸门调度，提供了很好的决策依据。

在实际运行过程中，为有效保障水情观测数据的准确性，运行管理单位应定期组织对渠道水位计、流量计等进行率定，以消除系统观测误差。同时，渠道水位计、流量计等作为电子观测设备，其观测数据受水流波动等因素影响，存在不同程度的跳变现象，当前虽在数据观测过程中进行了一定的滤波处理，但在滤波算法和处理效果上仍需进一步研究。另外，结合本文方法及结果试用，可尽快完成其余节制闸的过流公式率定及曲线绘制，以满足南水北调中线工程日常通水运行调度需要。