“多疑”出正解——三角函数中角的范围的界定

☉苏州外国语学校 孙龙华

一、考题再现

【题目】如图1，在平面直角坐标系中，以x轴为始边作两锐角α，β，它们的终边分别与单位圆交于A，B两点，且A，B的横坐标分别为，求（1）tan∠AOB的值；（2）α+2β的值.

图1

【考题分析】本题主要考查三角函数的定义、两角和与差的正切公式、二倍角公式以及特殊角的三角函数值等相关知识.对于问题（1），根据题意可知，然后根据同角三角函数关系式中的平方关系式，可求得sinα，sinβ的值，这样tanα，tanβ的值就有了，而tan∠AOB=tan（β-α），依据两角差的正切公式展开即可求得答案；而问题（2）要求α+2β的值，由于角α，β并非特殊角，所以只有整体求值，通过计算α+2β的三角函数值，间接求出α+2β的值，本题中选取求正切值较为妥当.

【学生错解】（1）因为α，β的终边分别与单位圆交于A，B两点，且A，B的横坐标分别为，所以.又由题意知，α，β均为锐角，所以.所以.所以

【错解分析】学生的解答过程中，第（1）小题没有错误，是正确的，第（2）问的解答是错误的，在考试的时候，很多学生都“栽”在第（2）问上，看似无懈可击的过程，其实反映了我们大多数学生在平时解题时的“缺心眼”.当结果求出时，我们要多几份质疑：怎么会解出两种情况？这两种情况都正确吗？要不要验证一下？如果不正确，是哪个环节出现了问题？当我们有了上述疑问之后，就会再去认真研究整个解答过程.既然出现了两个解，而整个解答过程的计算又没有问题，那就只有一种可能：角的范围过大，导致多解，沿着这个思路，我们验证的方向就明确了，下面我们一起来看一下第（2）问的正确解答.

【第（2）题正解】由（1）知，所以.因为，所以.因为，且α为锐角，所以，且β为锐角，所以.所以.所以.而tan（α+2β）=1，所以.

点评：根据三角函数值来确定角的大小，最为关键的是要确定好角的取值范围，而这其中有些题目给的范围恰到好处，在范围内只有正确解.可当遇到有些既给了三角函数值，又给了大致范围的题目，我们就要当心“陷阱”，当根据题设给定的范围求解出现多解时，一定要再根据三角函数值重新界定并缩小角的范围，去掉错误的答案，本题就是一个很好的例子.

其实这道考题是根据2008年的江苏高考题改编而来的，下面我们再来品味一下这道高考题.

二、品味高考

【2008年江苏15】如图2，在平面直角坐标系xOy中，以Ox轴为始边，作两个锐角α，β，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为

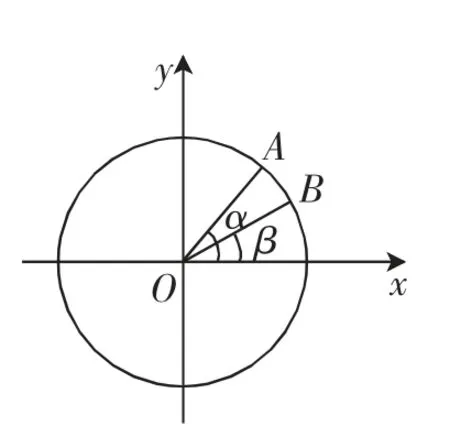
图2

（1）求tan（α+β）的值；（2）求α+2β的值.

【思路简析】第（1）问由三角函数的定义，知，而后根据同角三角函数关系式，分别求出，进而求得tanα=7，，最后利用两角和的正切公式，解得tan（α+β）=-3；第（2）问中，求得，因为，所以α+2β∈，从而

点评：这道高考题主要考查三角函数的定义、两角和的正切公式、二倍角的正切公式等.本题的考查，比上述考题的考查要容易很多，主要是题设数据比较巧，导致第（2）问中求得tan（α+2β）=-1，而，在此范围内只有一解.

在课本教材上的习题中，也有安排需要考虑角的范围的习题，在这里列出来，与大家一起体会编者的用意.

三、回味教材

苏教版数学《必修4》第123页练习题第3题：

【题目】已知，且α，β都是锐角，求α+2β的值.

【思路简析】此题就是“考题再现”中的考题的原型，其解法这里就不再赘述了.苏教版数学《必修4》第112页习题第12题第（2）题：

【题目】在△ABC中，已知，求cosC.

【学生错解】在△ABC中，易知C=π-（A+B），所以cosC=cos［π-（A+B）］=-cos（A+B）=sinAsinB-cosAcosB.因为，所以，所以，下面分两种情况讨论：

【错解分析】学生的解答过程看似非常完美、无懈可击，考虑得很是全面，其实错误还是出在角的范围的界定上，在题中，由必然要去算cosA，但是这时cosA有两种情况，这两种情况都符合三角形中角的要求吗？这是解题中出现多解时，我们必须要考虑的问题，故我们需要重新审定角A的范围问题.

【正解】因为，所以0°＜B＜90°.又因为，即sinA＜sinB，在△ABC中，根据正弦定理，有2RsinA＜2RsinB，即a＜b，所以A＜B.而0°＜B＜90°，故0°＜A＜B＜90°.再由可得，，于是

点评：本习题在新授课讲解时，绝大部分学生都是采用了【学生错解】中的分类讨论来做，根本没有考虑到角A的取值范围问题，归根到底，还是学生在考虑问题时不够全面.像这类在三角形中的求三角函数值的问题，一定要结合另一个角的三角函数值，来界定角的范围，切不可盲目地分类讨论.

三角函数中有关角的求值问题，是学生学习三角函数时的一大难点，在平时的学习中，我们要刻意加强这方面的训练，俗话说“熟能生巧”，只有多练、多写、多思，才能有效减少解题时出现的错误.