运用线性规划思想方法解决两元变量取值范围问题

☉江苏省昆山中学 沈艳虹

《普通高中数学课程标准（2017版）》提出了培养学生数学学科核心素养的课程目标，即“在学习数学和应用数学的过程中，学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等数学学科核心素养.”这是对2003版实验新课标提出的四基和四能目标的继承、创新、提升和发展.作为一名高中数学教师，除了在平时的教学实践中，把发展学生的数学学科核心素养贯穿于教学活动的全过程之外，更要分析研究并随时把握新课标下高考命题的新方向，即“命题应依据学业质量标准和课程内容，注重对学生的数学学科核心素养的考查.”唯有此才能引领学生取得素养发展和高考成绩的双赢.经过对近几年高考数学试卷的统计分析，笔者发现，简单的线性规划问题频繁地出现，其命题形式灵活，考查范围广泛，内容覆盖了方程、不等式、图像、坐标平移等基础知识.可以这样说，围绕简单线性规划来创设的问题情境已成为考查学生数学学科核心素养的载体，其中求线性目标函数在线性约束条件下的最值是常见题型，一般来说，学生只要把握线性规划的基本思想与方法就能顺利应答.但若题目在简单线性规划的基础上，对约束条件和目标函数做一些非线性的变换，则对学生的数学学习质量水平提出了较高的要求，该类题目具有较高的区分度，能体现高考数学的选拔功能.下面结合教学实践案例，就目标函数非线性和约束条件非线性下的两元变量取值范围的问题作初步的探讨与反思.

一、类型1：目标函数非线性

在近年的高考数学卷中出现了求目标函数是非线性函数的取值范围问题，此类题目情境多变，对考生的能力要求较高.常见的题型有以下几种：

【案例1】截距问题

解析：（如图1）令z=x2+y，则此式变形为y=-x2+z，z可看作是动抛物线y=-x2+z在y轴上的截距，当此抛物线与y=-x相切时，z最小.

故答案为72.

【案例2】比值问题

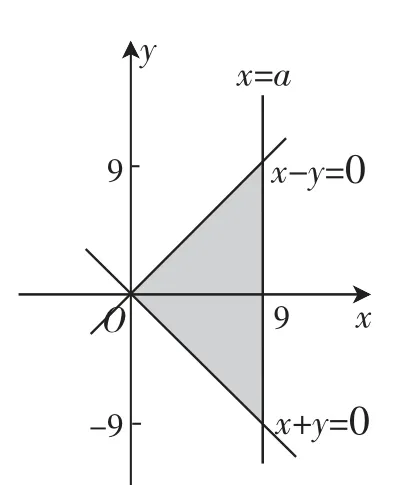
图1

解析：（如图2）是可行域内的点M（x，y）与原点O（0，0）连线的斜率，当直线OM过点取得最小值；当直线OM过点（1，6）时，取得最大值6.

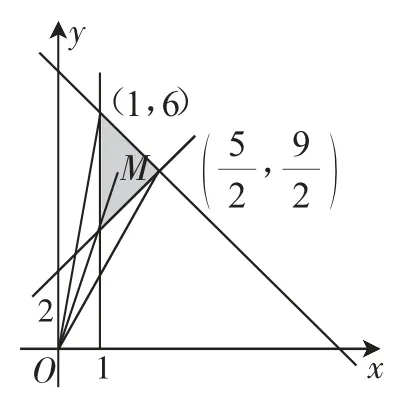
图2

【案例3】距离问题

当目标函数形如z=（x-a）2+（y-b）2时，可将z看作是动点P（x，y）与定点Q（a，b）距离的平方，这样目标函数的最值就转化为PQ距离的平方的最值.

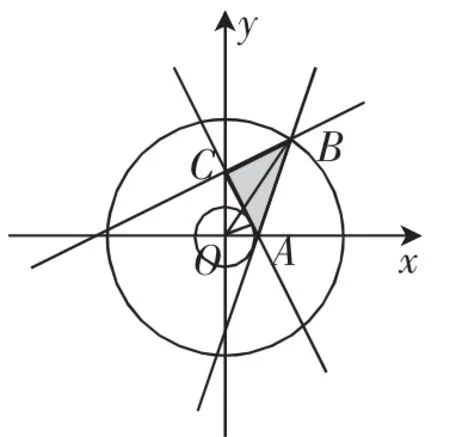
图3

解析：（如图3）作出不等式组表示的平面区域.

设x2+y2=z，则z是以原点为圆心的圆的半径的平方.

当圆x2+y2=z过点B（2，3）时取得最大值，

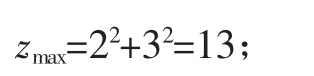
当圆x2+y2=z与直线AC：2x+y-2=0相切时取得最小值，从而z取得最小值.

设切点坐标为（x0，y0），则

【反思】从上述三个案例我们不难发现，当目标函数为非线性函数时，一般可以运用简单线性规划解决最值问题的思想方法去处理，所采用的方法和步骤也非常类似，其关键是先利用约束条件作出可行域，以确定目标函数对应的几何意义；然后根据其几何意义，利用数形结合的思想来求得其最值.这些问题主要考查学生的等价转化思想、数形结合思想以及运动变化思想等等，不仅考查了学生的作图、识图能力，还对学生的观察分析能力、联想与想象能力以及逻辑推理能力提出了较高的要求.

二、类型2：约束条件非线性

【案例4】已知正实数a，b，c满足c＞a，c＞b且=1，若a，b，c可构成某三角形的三边长，求c的取值范围.

错误解析：把条件c＞a，c＞b转化为a+b＜2c.

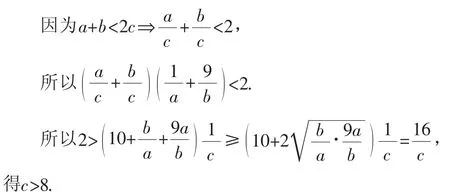
这个解法运用了不等式中常用的“乘1法”，很多学生认为这是个很巧妙的解法，然而，很显然在把条件转化为a+b＜2c时，此为一个不等价的转化，即c＞a，c＞b可以得到a+b＜2c，但反之不一定成立，所以求出来的c的范围可能发生了变化，所以这是一个错误的解法.

正确解析：，这样就能初步确定c的取值范围，进而假设a，b，c可构成某三角形的三边长，所以，还要满足a+b＞c这个条件，这又该用怎样的基本不等式才能解决问题呢？学生在运用不等式去解决该问题时遇到了困难.这时，如能结合题目中的已知条件，列出不等式组，则就可以运用线性规划的思想与方法来求得最终的答案.

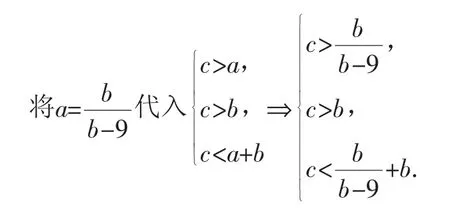
令c=y，b-9=x得

图4

作出图像（如图4）

可得y即c的取值范围是（16，+∞）.

【反思】当约束条件为非线性时，能结合所学的二次曲线、三次曲线等常见的函数图像作出不等式所对应的平面区域是解题的关键，也是解题的难点.此类题目蕴含数学中基本的优化思想方法，能很好地考查学生的数学学科核心素养.除了考查学生的数学基础知识、基本技能、基本思想和基本活动经验外，还对学生的综合分析能力、逻辑思维能力及解决实际问题能力提出较高的要求.所以在日常教学实践中，教师要联系学生的数学现实与生活实际，创设有效的教学问题情境，引导学生思维，利用信息技术呈现直观图像，以激发学生的学习兴趣，在夯实学生四基与提升学生四能的过程中，发展学生的数学学科核心素养.

综上案例分析，我们不难发现，线性规划思想能够很好的解决这类取值范围问题，前提是题设为两元不等式组，并能够作出相应的可行域，再从中提炼出目标函数的几何意义，然后利用数形结合思想，从而解决了基本不等式不能解决的最值问题.