破解一道2019年中考几何拉档题的视角分析与应对策略

(邮编：241002)

安徽省芜湖市南瑞实验学校

2019年安徽省中考数学试卷颇有亮点，特别是选择题的第7题，虽然题序靠前，构图简洁，数据简单，但还是让许多学生早早就遭遇了“拦路虎”，耽误了很多时间，甚至许多平时水平较好的学生思路也一时无法打开，有的甚至不得已，用作图的方法按比例放缩“量”出了答案，无形中这道小题居然成为了卷面的拉档题.

下面我们从不同的视角予以探究分析，并提炼出应对策略，以供参考.

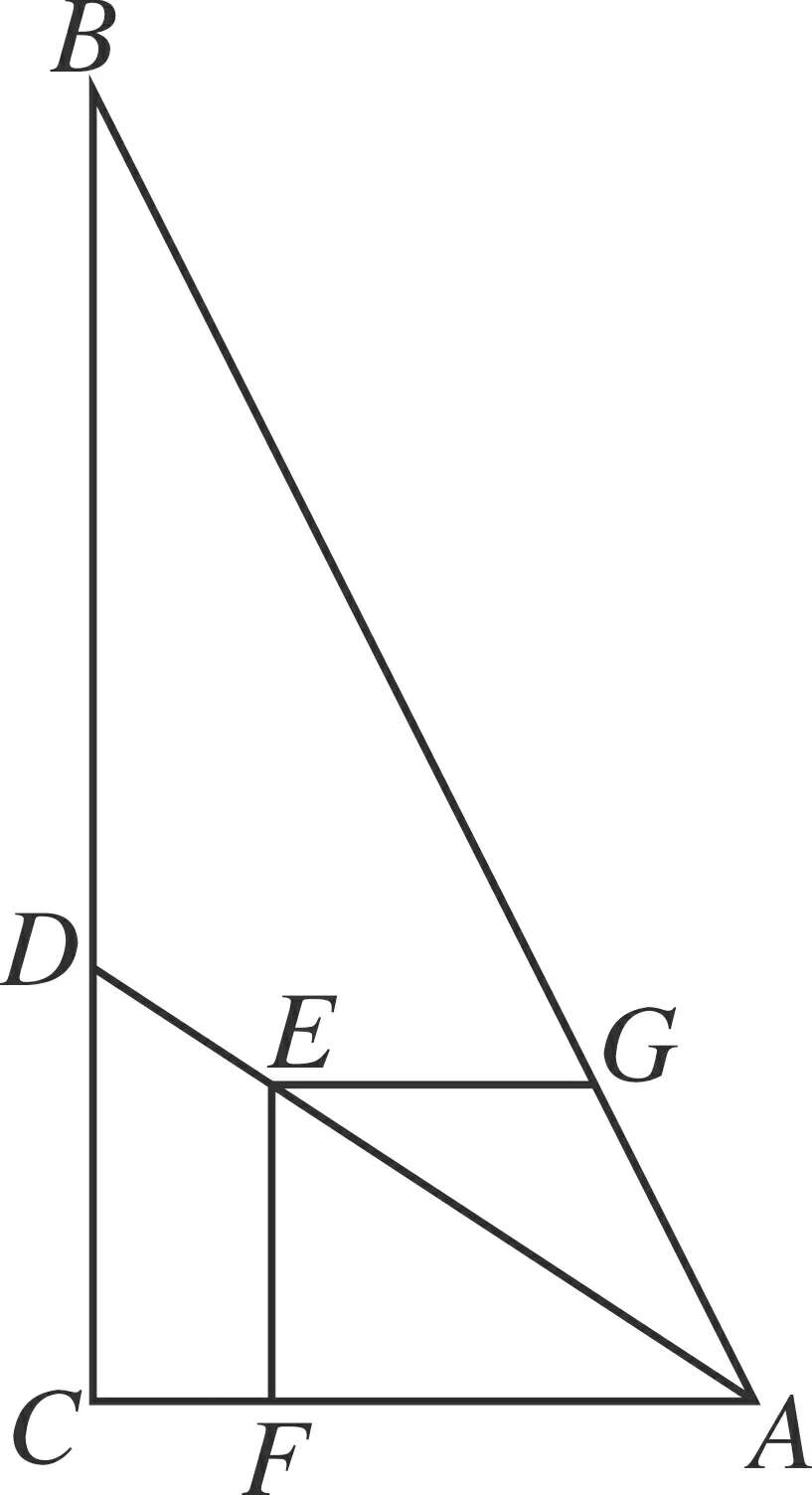
图1

题目如图1，在Rt△ABC中，AC=6，BC=12.点D在边BC上，点E在线段AD上，EF⊥AC于点F，EG⊥EF交AB于点G.若EF=EG，则CD的长为( )

A.3.6 B.4 C.4.8 D.5

1 初步审题 遭遇困惑

由∠C=90°，AC=6，BC=12，可知△ABC是确定的，即形状与大小均确定.D点是主动点在边BC上运动，随着D的运动，DA在变化，E在线段AD上运动，位置不确定，但始终保持EF⊥AC，EG⊥EF的位置关系，在运动变化过程中的某个瞬间有EF=EG，此时D点的位置是确定，故而CD的长可求.

明确了题意之后，如何寻找解题突破口仍旧没有突破.困难之处在于，点D与点E都在运动，EF=EG这个条件有什么作用，和已知条件之间有何关联，都颇费思量.

图2

2 基于不同视角的分析

2.1 几何变换视角 条件转化

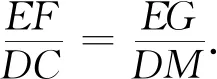
这样把EF=EG的条件就自然转化为DC=DM.接下来就是我们都很熟悉的基本问题了.

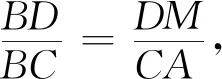
类似的，我们有

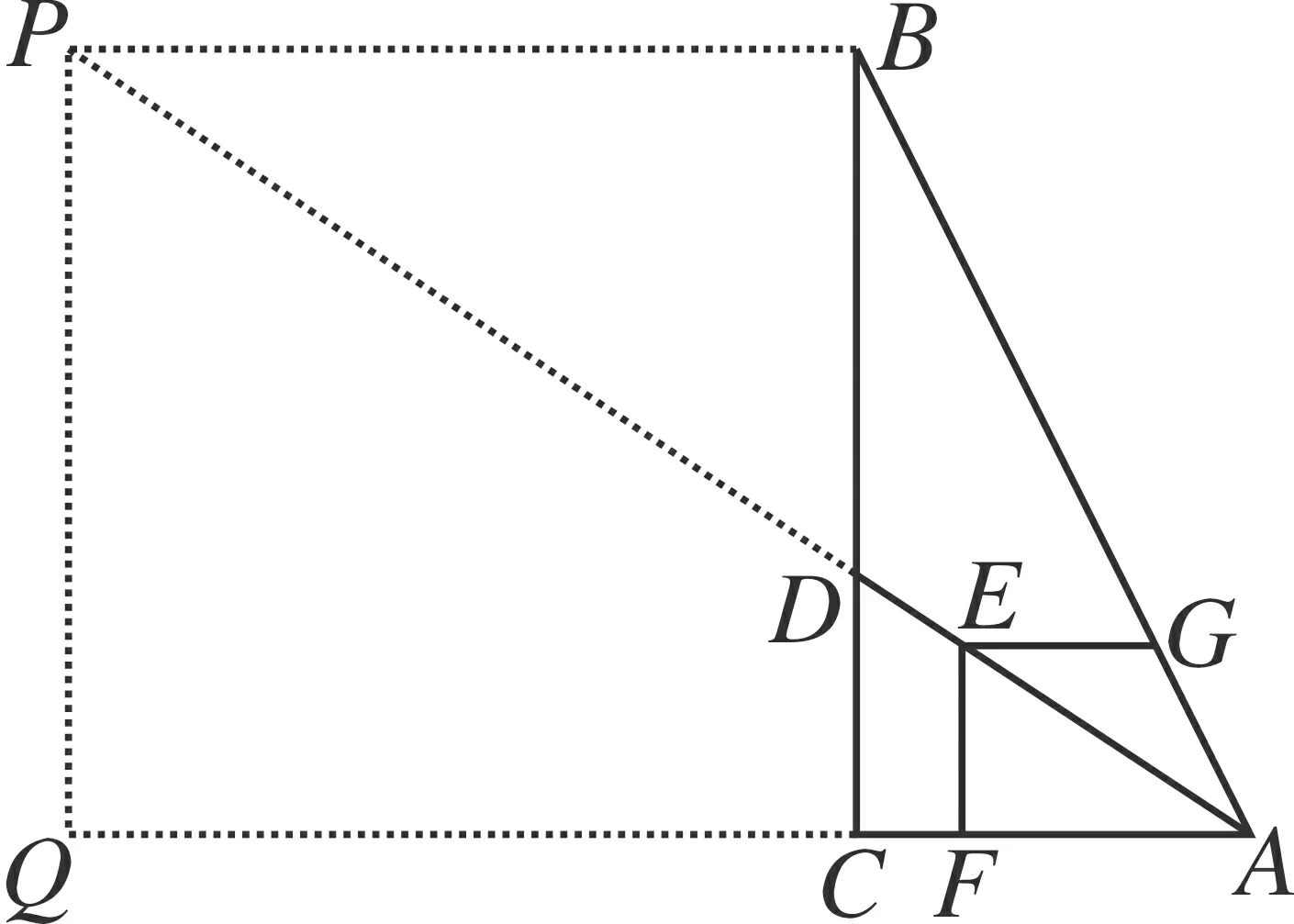
图3

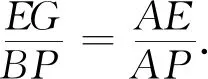
2.2 三角函数视角 列式消参

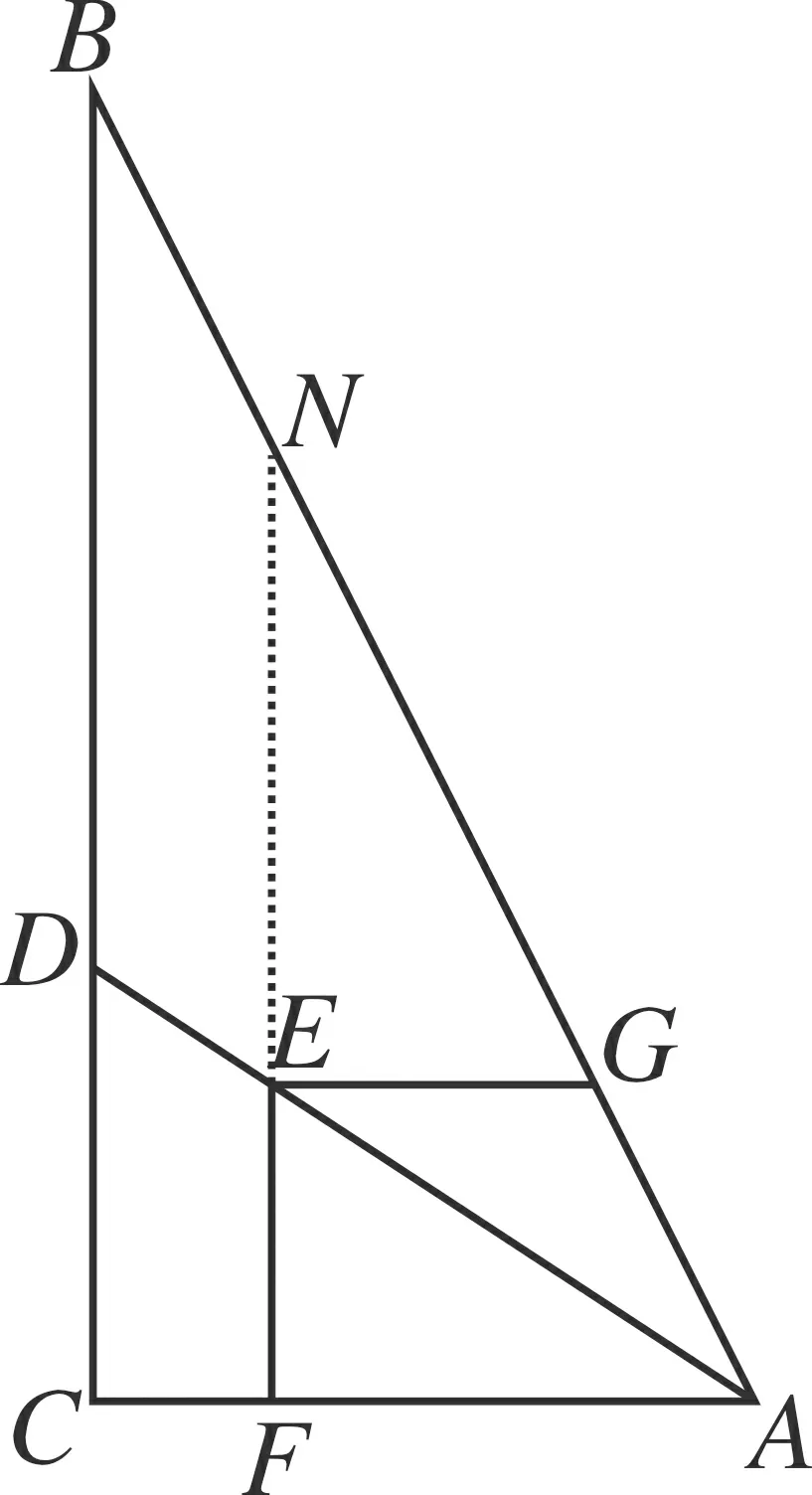
图4

考虑到tan∠BAC=2是定值，如图4可以延长FE交AB于N点.

法3 因为EG∥AC，所以∠EGN=∠BAC，所以tan∠EGN=tan∠BAC=2.

设EF=EG=k，则EN=2k.

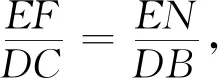
由上述三种方法，我们发现，虽然D和E都是动点，但是只要D的位置确定，E点分线段FN的比就是固定的，由tan∠BAC的值，可知NE与EG倍比关系，因此我们可以设定EF与EG的数量关系，就能源源不断编出新的题目.

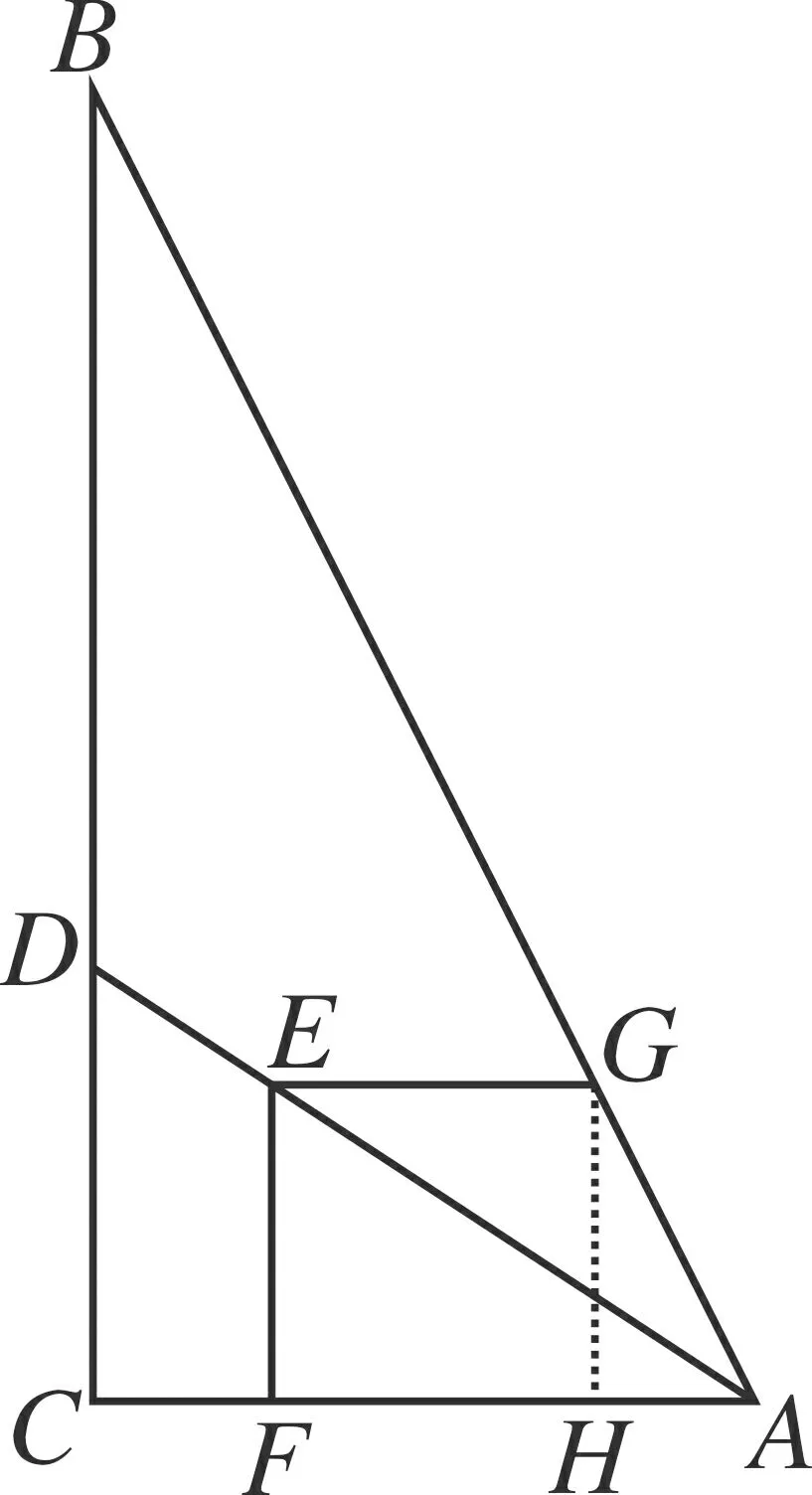
图5

法4 如图5过G作GH⊥AC于H点. 因为EF⊥AC，EG⊥EF，EF=EG，则四边形EFHG是正方形.

由tan∠BAC=tan∠GAH=2，可设AH=k，GH=EF=FH=2k，则AF=k+2k=3k.

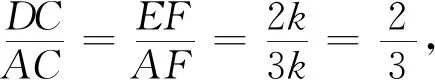
2.3 一次函数视角 待定系数

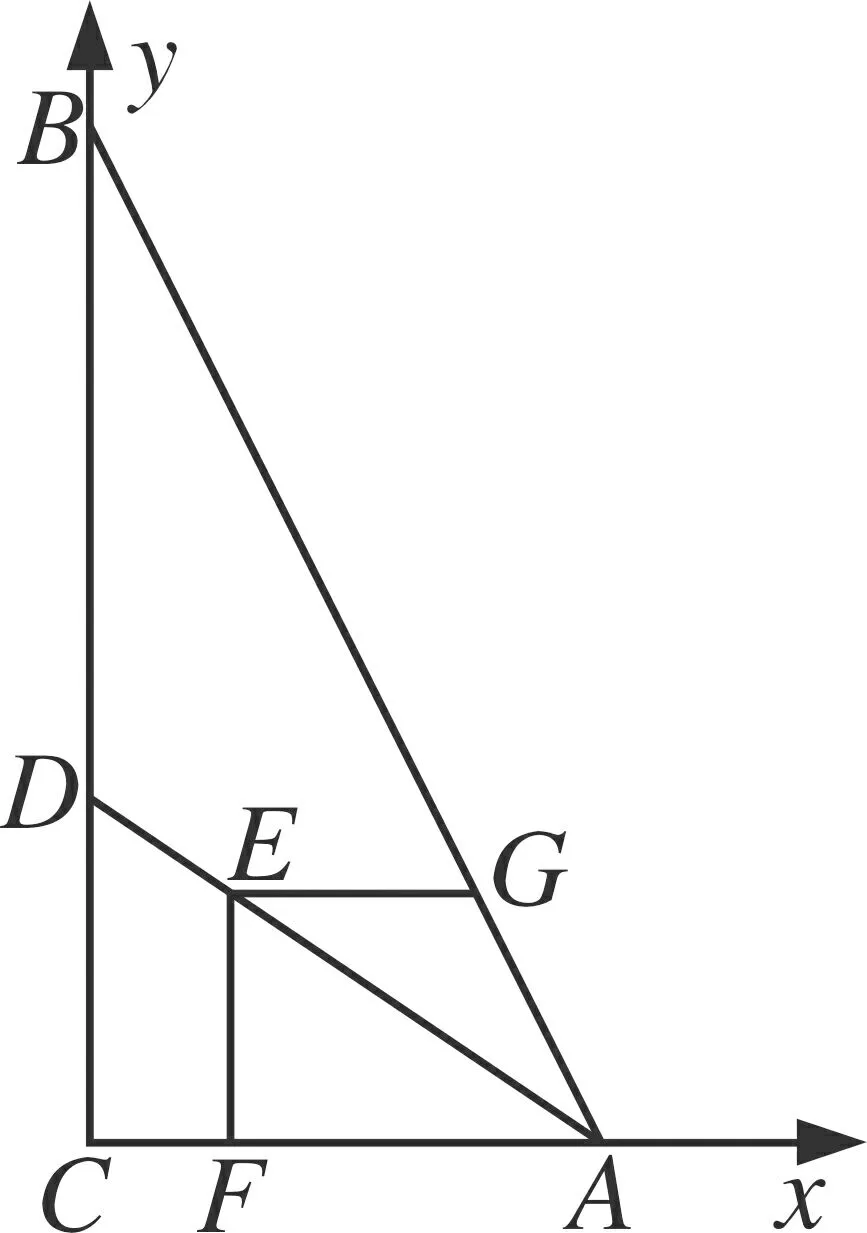
图6

法5 考虑到∠C=90°，且AC=6，BC=12，以C为原点，CA和CB所在的直线分别为x轴、y轴建立如图6的平面直角坐标系，则点A为(6,0)，点B为(0,12)，设直线AB的解析式为y=k1x+b1,可得k1=-2,b1=12.

因为G在直线AB上，可设G坐标为(t,-2t+12)，由题意yG=EF=EG=-2t+12，

所以xE=xG，GE=t-(-2t+12)=3t-12,yE=yG=-2t+12.即E点坐标为(3t-12，-2t+12).

设直线AE的解析式为y=k2x+b2,可得

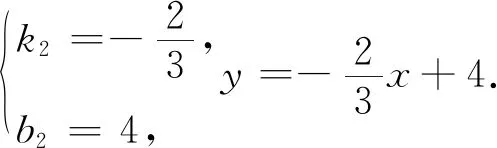
2.4 构建方程视角 设而不求

图7

法6 如图7，延长GE交BC于K，设EG=EF=KC=a，KE=b，DK=c.

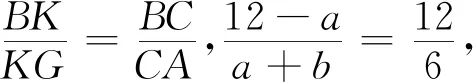
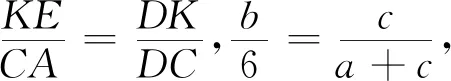
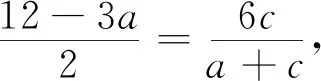
3 回顾与反思

回到问题的开始，本题困难在于EF=EG这个条件有什么作用，以及和已知条件之间有何关联，可以发现如果拘泥于某一个知识点，比如说“边等找全等”，或者局限于就几何论几何，而不能跨界思考，再加上考场心理紧张，思维打开确实有点困难.上述不同视角的破解分析，源于平时的积累与反思，将EF=EG放到不同的知识背景中就有可能产生不同的理解，从而展开由此及彼的推理，发挥关键条件的核心作用，攻坚克难.

由此，对我们的教学有以下启示：

3.1 复习阶段要注意对考生的心理疏导

现行中考虽然是初中学业水平考试，但同时肩负有高一级学校的选拔功能，对心智尚不太成熟的初三学生来说，压力很大.教师指导复习时，除了要进行知识梳理、优化结构、提炼方法、显化思想，还要有意识地进行考试心理疏导，让学生能以合理的预期对待考试，遇到平时不太常见的问题，能有效地平复躁动的心境，能合理地掌控时间和积极地应对，比如先用特殊位置、作图估算等尝试，待第二轮解答时再重点冲刺，以免过多纠缠，影响正常发挥.

3.2 坚持以核心素养的提升作为教学的落脚点，不能被 “绑架”

近年来，安徽省中考数学试卷命题不落俗套，稳中出新，平和而有力度，特别是第9、10、14和23题等固定题位的命题质量尤为上乘，具有广泛的美誉度.但是，由于客观上存在的应试指挥棒，每年市场上针对上一年真题的高仿卷、定心卷、逆袭卷等甚嚣尘上，花样百出.各级各类的模考，也是紧跟其后，于是无形中就形成了一股洪流，大家都围绕上述所谓热点(如最值、动态函数图象、操作型几何多解问题等)进行狂轰乱炸，且不说是否和当年考试对路(比如今年的试卷)，但是有一点是明显的，就是忽略了中考复习的全面性、全体性以及复习教学行为的最终目的——让学生真正经历数学问题的发现、分析与解决的过程，并在此过程中核心素养得到提升，而不是通过不断刷题形成“肌肉记忆”.

3.3 用辩证的态度对待“解题套路”

学生通过初中三年的系统学习，积累了大量的解题套路.一些特征明显、可操作性强的解题套路，直接上手，可以减少思考的逻辑链，缩短思考的时间，效率较高，但带来的负面效应就是学生解题只凭感觉，缺少反思的意识和能力，容易固化思维形成路径依赖(如上面提到的，部分学生看到线段相等只能想到全等)，长此以往就会形成思维定势，数学思维缺乏灵活和变通.因此，复习教学要倡导一种不唯书、不唯上、不唯套路的课堂氛围，鼓励学生既要总结适合自己的解题套路，又要能跳出固有思维，用全息化的视角去审视问题.相应地，教师备课时则要在问题的选配、变式的拓展、本质的挖掘上做足文章，力求以点带面，以少胜多.