高三解析几何解题教学中的几点做法

(邮编：230601)

安徽省合肥市第三十二中学

1 问题背景

在2018年高三二模考试前的月考和平时试卷批改中，笔者多次发现数学解答题得分较少的是第20道题——解析几何.

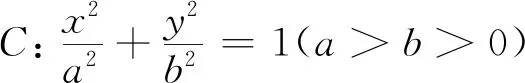
(1)求椭圆C的标准方程；

(2)若不经过椭圆C的右焦点F的直线l:y=kx+m(k<0,m>0)与椭圆C交于A、B两点，且与圆x2+y2=1相切.试探究△ABF的周长是否为定值，若是，求出定值；若不是，请说明理由.

从答卷上来看，有的同学只做了两问中的第一小问；有的对第二小问也只是写了一点点，如联立一个方程组，搭了个简单的框架就不了了之，能做完的同学为数极少.

2 原因探究

解析几何作为高中数学的重要板块，承担着培育学生数学的两大核心素养，即逻辑思维和计算能力的重任，作为数学老师在学科教育上应抓住高三全面复习的契机着力落实，这不仅仅是为了高考的得分，更重要的是为学生的后续学习.为此，高三年级组对不同层次的学生就这种现象进行了座谈.根据座谈的结果，我们将学生分成以下三类：第一类学生只会做第一问，对第二问由于缺少逻辑推理能力而不知如何下笔，建构不了知识框架；第二类学生明确解题方向，能搭建解题框架，但因为计算方法选择不当，计算过程过于繁琐，导致无法将计算坚持到底；第三类学生有较好的计算能力，但由于缺少必要的训练，在解题中缺少必胜的信念，从而框架搭好了就此搁浅.

针对学生解题中出现的这些问题，教师如何教学才能改变解析几何解答中出现的荒芜局面呢？

3 改进措施

现将年级组老师们的建议总结提炼后，提出要从信念、框架、计算这三个方面着手来改进解析几何复习教学，改变以前为赶复习进度而忽视学情的讲授式模式.为此，在后期的复习中，我们采用了以下流程来帮助学生攻克解析几何：首先通过简单题来夯实双基，帮助学生坚定信念增强信心；再用分层框架来破解典例；掌握常用技能简化和优化计算；最后进行对点强化训练.下面用实例来阐述具体的做法，以与同仁共享.

3.1 坚定信念 增强尝试信心

解析几何因计算难而让不少师生制定了这样的备考策略：第一问必做，对第二问如果难就选择放弃.在这样的指导思想下，即使看似难题，但稍加努力就能解决的问题也会因此而空缺.

波利亚曾说：“认为解题纯粹是一种智力活动是错误的，决心和情绪所起的作用很重要，教学生解题是意志的教育”.同时越来越多的研究表明：动机和信念在问题解决过程中同样有重要的意义.笔者赞同以上观点，认为解析几何复习中帮助学生树立战胜困难的信心比框架、计算显得更为重要.如对于问题背景中的第(2)问，教师可以在学生已做出(1)问的基础上，鼓励学生用数学语言去翻译：①直线l与C相交和②直线l与圆x2+y2=1相切这两个条件.至于这两步得出的结论怎么用，教师可以先不说.再引导学生尝试去写△ABF周长的表达式.这时学生会遇到如何表示|AB|、|AF|和|BF|的困难.教师适时点拨，进一步引导他们怎样利用前两步，这样逐步引导他们尝试去解决.让他们在实践中积累解题经验，在问题解决中体验成功的快乐，在战胜困难中坚定信念.

爱因斯坦说得好，他认为信念最好能由经验和明确的思想来支持.这说明除了有意识，还要有活动经验，而经验的获得来自于大量的实践.信念的培养不是老师几句鼓励的话就能树立的，它需要有扎实的基础，教师的有效示范，学生的积极内化和有素的训练来支撑.

3.2 搭建框架 明确解题方向

(Ⅰ)求C的方程；

(Ⅱ)设直线l不经过P2点且与C相交于A、B两点.若直线P2A与直线P2B的斜率的和为-1，证明：l过定点.

做法剖析：

(1)根据逻辑关系，搭建分层框架，对本题的第二问采用分析法执果索因.

寻结论成立的条件，步步为营理清解题思路，消除解题的盲目性，增加解题的信心.通过化整为零，将解题过程分成若干层.根据层与层之间的逻辑关系建立起框架，然后自下而上进行书写.具体如下：

(2)理清条件关系，翻译每层内容

为了表达的需要，引导学生大胆设出未知量，将题中的条件关系用数学符号或式子来表达，在框架的指引下理清k和m的逻辑关系，朝目标方向努力.

第一层：特殊情况验证.

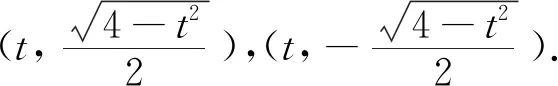
一般情况证明：

联立方程，得出两点间坐标的关系，用两点的坐标表示斜率和.

设l：y=kx+m(m≠1)，A(x1，y1)，B(x2，y2).

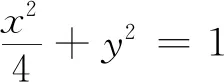
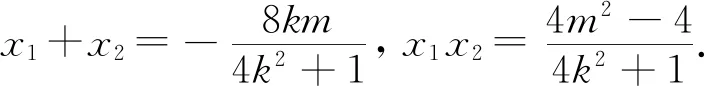
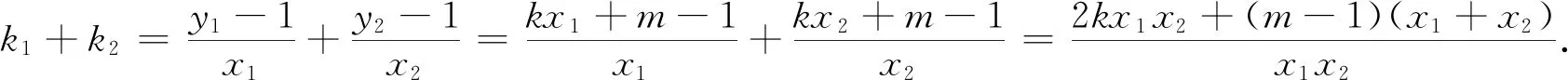
第二层：利用韦达定理，根据斜率和为-1，寻找k与m的关系式.

第三层：消去k，将其方程化为点斜式，从而得出定点.

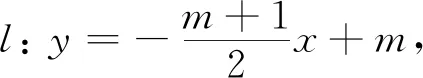
(3)对点练习，训练思维 选择相应的模拟题，让学生分析，进行解题前逻辑思维训练.采用独立思考，畅谈解法,优化解法这样的课堂活动来激发学生的解题热情，开发学生解题潜能.

3.3 简化计算 助推正解得出

解析几何的特点是计算难，如果计算方向不明确，方法繁杂会导致整个解题全盘崩溃.因而当学生面对问题时，首先要引导学生多想少算，明确计算对象，优选解题方法，设计合理的运算途径.框架构建好后，要求学生再想一想，寻找恰当的计算方法，以便简化运算过程而获得优解.常用的简化计算方法有：追根溯源，回归定义；平面几何渗透，数形结合；设而不求，整体运算；利用韦达定理化繁为简等.

图1

(Ⅰ)当t=4，|AM|=|AN|时，求△AMN的面积；

(Ⅱ)当2|AM|=|AN|时，求k的取值范围.

做法剖析 (Ⅰ)解略；(Ⅱ)条件中|AM|和|AN|都是弦长，因而需要利用弦长公式，于是联立方程求出|AM|.为简化计算，再利用MA⊥NA，在|AM|已得出的基础上，直接求出|AN|.

(1)设而不求，整体代入

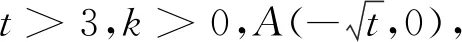
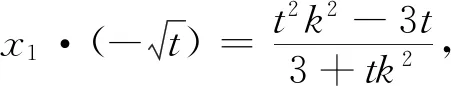
(2)利用垂直，避免重复

(3)挖掘隐含条件，建立不等关系

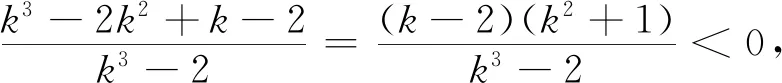
(4)对点练习，强化计算

让学生在练习中逐步掌握运算技能，在计算中磨练意志，消除对解几的畏惧心理.

(1)求椭圆C的标准方程；

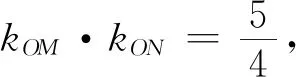
4 改进后的反思

在框架分层式的解题解学中，框架有助于学生按照逻辑关系寻找解题方向，

分层有助于梳理条件，分解难点.而一些简化计算方法的掌握便于学生优化计算，使计算变得更流畅.对点训练让学生从解题的模仿开始，逐步训练思维和提高计算能力.通过一段时间的训练，取得了一定的成效.从学生的答卷来看，回答解几大题第二问的同学越来越多，能坚持做完的同学也多了起来，该题年级平均得分在逐步提高.在尝试的过程中，感触较多，反思感悟可总结成以下三点：

反思一不愤不启，学会忍

不愤不启是指不到学生们想弄明白而还没有弄明白时，不去启发他.在课堂上我们经常看到学生解这类题会跑偏，出现一开始解题方向不对，选择的计算方法过于繁琐，跌跌撞撞艰难向前的现象.这时的老师要学会忍，不要马上就呈现解答.要让学生在挫折中探索解题方向，以便能更好地磨练他们计算耐力，让他们更深刻地去体会计算背后的算理.启发时先多问问学生是如何想的，为什么这样想，然后贴近学生的认知去启发.切不可急于兜售自己的想法，而掐灭学生思维的火花.

反思二不舍不得，学会放

对解析几何的复习，教师要敢舍，认为多讲一些题型，学生就能搞好是老师们的一厢情愿.对学生解题思路和计算能力的训练，虽然开始训练时很费时间，但教师也要舍得把宝贵的课堂时间放手给学生去尝试，即便一堂课只解决一道题,只要学生能真正理解掌握也是值得的.授之以鱼不如授之以渔，没舍就没有得！

反思三不急不躁，学会听

一道解析几何题，它的的解法往往有多种.教师的解法不是权威，我们要放下权威，更多地去关注学生的想法.借学生的口让各种解法“百花齐放”起来，让他们在思维碰撞中寻找最优解.即使学生的解法很拙劣，教师也要不急不躁，耐心去倾听，呵护学生参与思考的积极性.

总之，对解析几何的复习，我们既要从意识层面去落实，调动学生的一切非智力因素的参与；又要从实践层面上加以夯实.用信念、框架和计算这样的三套车齐驱并驾我们高三解析几何的复习，相信一定不会辜负“把立德树人作为教育的根本任务”的历史使命！