素养视域下数学能力的考查——2019年全国高考数学(理科Ⅰ卷)部分试题分析

(邮编：237331)

安徽省金寨第一中学 六安市徐道奎名师工作室

2019年全国高考数学(理科Ⅰ卷)试题的学科特色突出，素养导向明确，对素养视域下数学能力的考查较为全面.试题有以下特点：对必备关键能力的要求更强，对创新能力的要求更强，对应用能力的要求更强.注重考查学生的探究实践能力，发现、提出、分析和解决问题的能力，适应新情境以及在新情境中获取信息能力，阅读理解能力，迁移联想能力，对数学符号语言的理解转化能力，逻辑思维和思维转化能力等等，融综合性、应用性、创新性于一体，注重数学文化与数学教育的高度融合.实现了“从能力立意到素养导向”的转化，本文仅以学生普遍反响较为强烈的几个问题为例予以分析.

1 全方位的能力考查

1.1 数学需要探究和实践，要有在探究中发现问题的能力

素养视域下的探究发现是一种主动、自觉的活动，是一种习惯、意识的使然，是自主发现、提出、分析和解决问题的行动过程.

题1 (第12题)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E、F分别是PA、AB的中点，∠CEF=90°，则球O的体积为

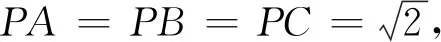
解决数学问题需要主动的观察、分析、尝试，这就是探究，探究没有固定的模式.探究活动要以关键条件切入，以条件如何运用找到契机，如：作出三棱锥的高，在此基础上尝试、摸索.探究是感知、发现隐含信息的基本方法.探究过程需要不断地迁移联想，不断地提出问题，条件有什么用？为什么要给“这个”条件？条件能否转化？转化后又可发现什么，得出什么？回到本题，立体几何中的“垂直关系”非常重要，是否隐含其它的垂直关系？具体地，能否通过“中点”、∠CEF=90°和PA=PB=PC得出新的“垂直关系”？怎样得出？

学生解题的障碍是：习惯于思路明了、直觉就能做出判断的问题，对于条件和关系隐含的问题“无从下手”，缺乏探究经验，不知道运用条件深入分析，发散思维，不能够迁移联想，比较分析.当然，探究发现不是“无中生有”，不是“空中楼阁”，而是建立在一定的基础知识、基本能力、基本思想和基本活动经验之上的数学活动.

1.2 数学需要适应情境，要有在新情境中分析问题的能力

高考要体现时代精神，要创新，要与时俱进，跟上时代潮流，“对创新意识的考查是对高层次理性思维的考查”，“在考试中创设新颖的问题情境，构造有一定深度和广度的数学问题”是今后考查的方向，毫无疑问，素养视域下的能力考查，更需关注创新能力、创新意识和创新精神，而新情境、新背景是考查创新能力的重要载体，在新情境中用数学解决实际问题是数学价值的体现.

题2 (第21题)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别为α和β，一轮试验中甲药的得分为X.

(1)求X的分布列；

(2)若甲药、乙药在试验开始时都赋予4分，pi(i=0,1,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…，7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1).假设α=0.5，β=0.8.

(ⅰ)证明：{pi+1-pi}(i=0,1,…,7)为等比数列；

(ⅱ)求p4，并根据p4的值解释这种试验方案的合理性.

题目具备创新能力考查的三个特点：新的角度，新的情境，新的知识组合方式.对于具有实际意义的情境问题，如何把实际问题数学化？需要进行数学抽象，分析问题中的关键要素，建立数学模型.

第一问：求一轮试验中甲药得分的分布列，根据题目设置和约定，容易分析甲药在一轮试验中得分有三种的可能，即：-1、0、1，概率分别是：(1-α)β、αβ+(1-α)(1-β)、α(1-β).

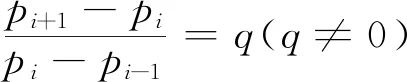
平心而论，本题并没有学生反应的那么难，但学生为什么怕？第一，不能适应新情境，不能理解新情境.情境是广义的概念，包括自然情境，实践情境，学术情境等等.情境陌生，融入不了.不明白题目要表述的是什么事？第二，缺乏在新情境中阅读、获取信息的能力，很多学生根本读不懂题目，不理解题目表述的方法去对比药效.第三，也是最关键的，对数学学科语言的理解转化存在障碍，数学符号语言不能“翻译”为通俗的自然语言，如：怎样用随机变量表示试验结果？“pi(i=0,1,…,8)表示甲药的累计得分为i时，最终认为甲药比乙药更有效的概率”是什么含义？pi=api-1+bpi+cpi+1(i=1,2,…7)有什么作用？第四，缺乏把实际问题抽象为数学问题的基本素养，缺乏灵活运用数学知识的能力.如：第二问实际上就是一般的数列问题，构造法证明等比数列和累加法求数列通项问题，情境(学术情境)变化了(不在单一的数列问题里面)，就无所适从.

素养视域下的数学考查将逐渐从“学科知识化”转变为“真实情境化”，因此，适应、理解新情境至关重要，呆板、机械、僵化的知识将无用武之地.“情境化”不是“去数学化”，而恰恰更能发挥其应用价值、实践价值和社会价值.所以，我们要强调培养学生适应新情境，在情境中分析问题的能力，培养情境中的问题意识和灵活、综合解决问题的基本素养.

1.3 数学需要科学的思维，要有在不断推理转化中解决问题的能力

对逻辑思维能力的考查贯穿于整个试卷的始终.数学是思维的体操，是思维的科学，解决数学问题离不开科学的思维，离不开逻辑推理和抽象概括.数学问题的解决需要不断地把条件、结论进行分解组合，变式转化，这就是数学推理，当然，主要是逻辑推理.

题3 (第20题)已知函数f(x)=sinx-ln(1+x)，f′(x)为f(x)的导数.证明：

(2)f(x)有且仅有2个零点.

分析(1) 求f′(x)的极大值点，实际上只要分析f′(x)的导数f″(x)的变号零点，可通过对f″(x)再求导，证明f″(x)单调，结合零点存在定理得出.

(3)f(x)的零点可按照f″(x)→f′(x)→f(x)路径分析，思维不断地进行转化，直至得出结论.推理要锲而不舍、严密周全，从二阶导数的单调性、二阶导数的正负，到一阶导数的单调性、一阶导数的正负，到原函数的单调性、零点，一步一步的分析.

学生解题的障碍是：缺乏思维的条理性，由高阶导数逐步分析原函数的思路不清，目标不明确.

素养视域下的思维能力既是一种能力，也是一种品质，更反映了一种严肃的科学态度和科学精神.

1.4 数学需要学科贯通和领域融合，要有在文化背景下进行数学抽象的能力

高考是综合能力素养的考查，全国一卷试题充分体现了数学的科学价值和人文价值和社会价值.

题4 (第4题，试题略)把数学美、艺术美和数学运用充分结合起来，把实际问题抽象为数学问题，虽然不是难题，也容易出错，问题出在是否理解生理学意义“腿长”的定义，跨学科的知识对问题解决非常重要.素养视域下的能力考查，要适应“试题条件从结构良好到结构不良”，“试题要素从单一因素到复合因素”的变化，要学会批判、判断、选择和分析.

数学在体育中运用也非常广泛，第15题是涉及体育比赛规则的概率问题.

题6 (第15题)甲、乙两队进行篮球决赛，采取七场四胜制(当一队赢得四场胜利时，该对获胜，决赛结束)，根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4:1获胜的概率是______.

问题抽象为独立事件同时发生的概率.首先要充分理解题目，如：比赛的规则，要根据题目的表述结合实际理解，注意主客场获胜概率的不同，甲4∶1获胜的含义.有的学生没有理解比赛的规则，把4∶1取胜理解为5场比赛胜4场，发生错误.

素养导向的能力考查要求学生关注生产生活，关注社会，有宽广的知识面，能把实际问题抽象为数学问题，能以科学的方法和数学原理解决实际问题.

2 新高考对教学的启示

高考是教学的风向标，考试制度的改革对数学教学提出了新的要求.高考命题整体质量高，要充分发挥高考试题的教学导向作用，要透过高考考试风格和考试方向反思教学的不足，积极弥补和改进.

(1)有基础才能有潜能，提升能力素养的前提是扎实教学，夯实基础，因此，必备的基础知识必须加宽加厚，要全面而有深度地理解掌握基础知识.教学要回归概念，回归基础，整体把握数学学科体系，建立知识网络体系.

(2)不能依靠刷题来提高学生成绩.要让学生在理解数学、掌握原理的基础上获得“四基”，提高“四能”，以不变应万变.学生在解答本套试题中暴露很多问题，为什么能计算复数却不理解复数的概念(第2题)，会用参数的意义解题而不会消参(第22题)，能解情境熟悉的“难题”，却不能解情境陌生的简单问题(第4、6、15、21题)，是长期单一训练，机械做题，思维固化的结果.

(3)要认真研究课标，研究教材.2019年数学试题逐步由“实验版课标”向“2017版课标”过渡，放弃了三视图、线性规划的考查，有一定的道理.尤其三视图，从数学角度分析，其反映学生空间想象力作用并不明显，在备课组讨论时我们把该问题提出，但老师们不敢轻易放弃，平时练习和考试中的三视图问题偏、怪、难，意义不大，浪费了时间.当然，并不是今年不考的，将来不考，笔者只是强调要注意研究课标，注意课标的变化.

(4)注意素养视域下能力考查的变化，尤其是探究能力的考查，多引导学生解决开放型、组合型问题.注意情境的变化，提出问题方式的变化，考查目的变化.树立正确的教学观，要在培养学生自主学习能力(包括阅读理解能力)上下功夫.数学教学要重视学科观念，触及数学本质，追求有深度的教学，渗透数学思想，融入数学文化，坚持以人为本，立德树人，注重培养创新精神、创新意识和创新能力，养成科学的思维品质和思维习惯，在数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等方面培养学生的关键能力.

3 关于命题的几点思考

(1)数学文化包罗万象，数学概念的形成，数学思想方法的提炼，数学精神，数学美学，数学发展的曲折历程，数学家不屈不挠、孜孜以求、敢为人先的思维方法、探索历程和创新精神，中西方数学思想方法的差异等，都是数学文化.数学文化素材的选择要凸显数学历史发展的成果和过程，要积极向上，涉及的范围可以更广.

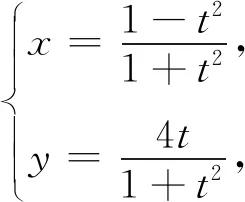
(3)概率或以概率为背景的试题(第6、15、21题)出现多次，虽说考查的内容不同，但是否有比重失调之嫌呢？基于高考选拔功能，函数及其性质(或者考查函数方程思想的试题)是否可以加大份额？

上述分析仅一孔之见，不足之处敬请专家同行批评指正.