两个旁切圆与半外切圆半径的平方型双边不等式
2019-09-04 07:12:58福建省闽侯县上街实验学校350100
中学数学研究(江西) 2019年8期
福建省闽侯县上街实验学校 (350100)
黄银珠
最近,笔者重新翻阅了《中国初等数学研究》,受益匪浅.其中杨志明老师于2016年发表的一文[1]引起笔者关注,经过探究,在文[1]的基础上,本文建立了两个涉及旁切圆与半外切圆半径的平方型双边不等式.
约定ΔABC三边长为a,b,c,其对应的旁切圆半径分别为ra,rb,rc,R、r与s分别为ΔABC的外接圆半径、内切圆半径及半周长.Σ表示轮换对称求和.
定义[2]与三角形两边延长线及其外接圆相切的圆,叫做三角形的半外切圆(即“远切圆”).ΔABC三边a,b,c对应的半外切圆半径分别记为Ra、Rb、Rc.其中Ra表示与AB,AC延长线及外接圆相切的圆半径;Rb表示与BC,BA延长线及外接圆相切的圆半径;Rc表示与CA,CB延长线及外接圆相切的圆半径.
引理在ΔABC中有如下结论成立:
(1)R≥2r(欧拉不等式);
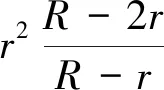
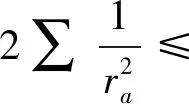
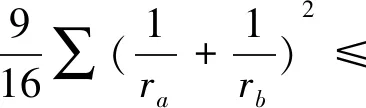
定理1证明:由文[1]可得恒等式
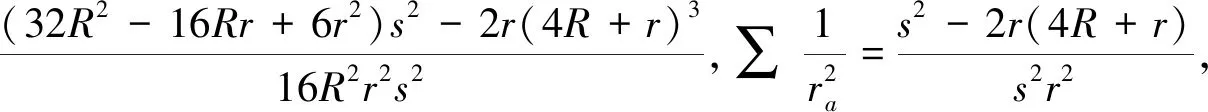
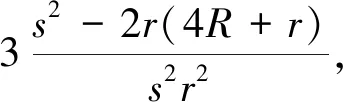
定理2证明:由文[1]得恒等式

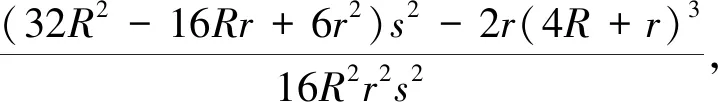
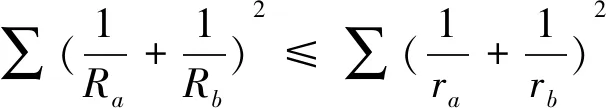

猜你喜欢
民族文汇(2022年23期)2022-06-10 00:52:23
中等数学(2021年2期)2021-07-22 06:21:52
科学家(2021年24期)2021-04-25 12:55:27
中等数学(2020年9期)2020-11-26 08:07:28
初中生学习指导·中考版(2020年4期)2020-09-10 07:22:44
数学物理学报(2019年4期)2019-10-10 02:39:12
中等数学(2018年7期)2018-11-10 03:29:04
周口师范学院学报(2018年5期)2018-09-28 08:49:16
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
语数外学习·上旬(2013年2期)2013-03-13 07:20:42

