一个求解旅行商问题的松弛算法

董传波

(中国航空油料集团有限公司，北京 100088)

旅行商问题(TSP)是运筹学领域典型的组合优化问题，其目的是在一个完全图G=(N,A)中找到费用最小的哈密顿回路。其中,N={1,…,n}表示城市构成的集合，A={(i,j)|i∈N,j∈N,i≠j}表示边构成的集合。TSP在实际中具有非常广泛的应用，例如，机组调度[1]、热轧调度[2]、采访日程安排[3]、自主移动机器人任务规划[4]、印刷机调度[5]等。由于TSP是一类具有二元决策变量的NP-hard问题[6]，启发式算法常被用于解决这类问题，包括蚁群算法、遗传算法、局部搜索、神经网络、模拟退火、禁忌搜索等[7-12]。然而，这类算法存在解的最优性无法保证、实际应用中的解释性不好等缺陷。因此，有必要设计TSP的全局最优求解算法[13-19]。

Dantzig等[13]首次提出了TSP问题的数学规划模型，即Dantzig-Fulkerson-Johnson(DFJ)模型。该模型除了包括决策变量的二元约束以外，还包括分配约束和子回路消除约束。然而，由于该数学模型的约束条件数量是城市数量的指数级，导致利用该模型在求解大规模TSP时变得不可行。因此，有必要构建只有多项式数量约束条件的TSP数学模型以提高求解效率。Miller等[14]提出了一个具有多项式约束数的混合整数规划模型来描述TSP。随后，Desrochers等[15-16]改进了该模型。混合整数规划问题通常可以采用分支定界法来精确求解。然而，由于受变量数和约束条件数量的限制，TSP可求解的问题规模仍然有限。

Sarin等[17]的数值结果表明，约束条件个数对求解TSP最优解起着至关重要的作用。虽然TSP具有指数级数量的子回路消除约束，但是大多数约束都是不起作用约束。研究有效的方法来给出起作用的子回路消除约束，可以潜在地加快TSP的求解速度。本文提出了一个求解TSP的松弛方法，通过求解一系列线性整数规划问题(LIP)来得到起作用的子回路消除约束，不断地把新找到的起作用子回路约束添加到松弛问题中，逐步实现TSP的精确求解。

1 数学模型

TSP的数学模型可以表述如下：

(1)

(2)

(3)

xij∈{0,1},∀i∈N,j∈N，

(4)

{(i,j):i∈N,j∈N;xij=1}不构成子回路，

(5)

其中，xij为0-1变量，表示路段(i,j)是否在最优的旅行路径中，即推销员是否通过该路段。cij表示从城市i到城市j所需要的花费。

目标函数(1)表示总的旅行费用最小；约束条件(2)～(4)为TSP的分配松弛约束，约束条件(2)和(3)意味着最优路径上任意一个城市都只有一条边进入和一条边离开，约束条件(2)保证推销员只能经过一个城市i到达城市j，约束条件(3)保证推销员只能经过一个城市j到达城市i；约束条件(4)表示变量xij是0-1变量；约束条件(5)用于避免子回路。该约束条件有不同的数学表述形式[13-16]。

在DFJ模型中，子回路消除约束可以表述如下[13]:

(6)

约束条件(6)具有城市数量指数级的子回路消除约束，但可以完全排除任何可能的子回路。我们提出的松弛策略生成的子回路消除约束是约束条件(6)的子集。

Desrochers等[15]提出了如下约束条件来代替子回路消除约束：

SDL={x:∃ {u1,…,un},u1≡0,使得

uj≥(ui+1)-(n-1)(1-xij)+(n-3)xji,∀i,j≥2,i≠j，

(7)

1+(1-x1j)+(n-3)xj1≤uj≤(n-1)-(n-3)x1j-(1-xj1),∀j≥2}，

(8)

当约束条件(8)是起作用约束时，约束条件(7)是最大平面定义[18]。

2 求解TSP的松弛算法

如下命题是本文提出的方法的理论基础：

命题1：对于满足分配约束条件(2)～(4)的任意可行解x=[xij,i∈N,j∈N]，可以把x分解为一组回路，且分解得到的回路数量不小于1。

证明：根据约束条件(3)，对于给定的任意一个节点i∈N，我们可以找到有且仅有的一个节点i1∈N满足xii1=1。这意味着推销员从城市i到达城市i1。同理存在一个节点i2使得xi1i2=1。以此类推我们可以得到一个城市序列Si=(i,i1,i2,…,im)，这个序列满足：xikik+1=1,∀k=1,…,m-1；i≠i1≠i2≠…≠im-1，其中，im∈{i,i1,i2,…,im-1}。当im=i就意味着Si是一个回路。该城市序列的生成保证了序列的存在性。如果m=|N|那么就只有一个回路，否则对于可行解x来说至少包含一个回路。特别地当m=1时节点i自身形成一个回路。证毕。

如果我们把约束条件(5)从TSP的模型中去掉，则TSP被松弛为了一个指派问题(AP)。我们可以采用匈牙利算法快速求解得到AP的最优解。如果得到的最优解只有一个回路，则该解也是TSP的最优解。如果AP的最优解包含多个回路，则需要在AP问题的基础上添加起作用的子回路消除约束。为了简化表示，我们令T表示已经生成的子回路集合，At表示子回路t上的路段集合，mt表示该回路上路段的数量。起作用的子回路消除约束表述如下：

(9)

把约束条件(9)加入到AP中，我们可以得到松弛的TSP。由于该松弛问题是线性整数规划问题，我们可以采用分支定界算法来进行求解。通过求解松弛问题，我们可以得到松弛问题的最优解。该解也可以分解成为一组子回路。如果得到的新的最优解中只有一个回路，则该解就是TSP的最优解。否则，将新生成的一组子回路加入到已经生成的子回路集合中。然后根据新的已经生成的子回路集合生成子回路消除约束(9)，形成新的松弛TSP，然后通过分支定界算法求解，重复上步骤，直到松弛的TSP的最优解只有一个回路，即得到TSP的最优解。

求解TSP的松弛方法的详细步骤总结如下：

Step 1 初始化。设已经生成的子回路集合C0=∅，将迭代次数设为k=0。

Step 3 求解松弛的TSP。求解得到松弛的TSP的最优解xk。

Step 4 生成子回路。把xk分解成一组回路，生成新的回路集合Tk。

Step 5 检验。如果新生成的回路个数|Tk|=1，则xk为TSP的最优解，停止迭代；否则，更新已经生成的子回路集合Ck+1=Ck∪Tk，设k=k+1，转到Step 2。

由于TSP的子回路消除约束的数量有限，本文提出的松弛算法具有全局收敛性。在我们的方法中，生成的子回路消除约束的个数随着迭代次数的增加而增加，最坏的情形是生成所有子回路消除约束。

3 算例分析

3.1 9个城市的TSP

考虑如图1所示的9个城市的对称TSP,我们通过城市的坐标来获取任意两个城市间的出行费用。通过求解AP，我们可以得到4个子回路：1→2→1、3→4→3、5→6→7→5和8→9→8。AP的目标函数值35.685。这4个子回路可以生成4个子回路消除约束：

x12+x21≤1，

(10)

x34+x43≤1，

(11)

x56+x67+x75≤2，

(12)

x89+x98≤1。

(13)

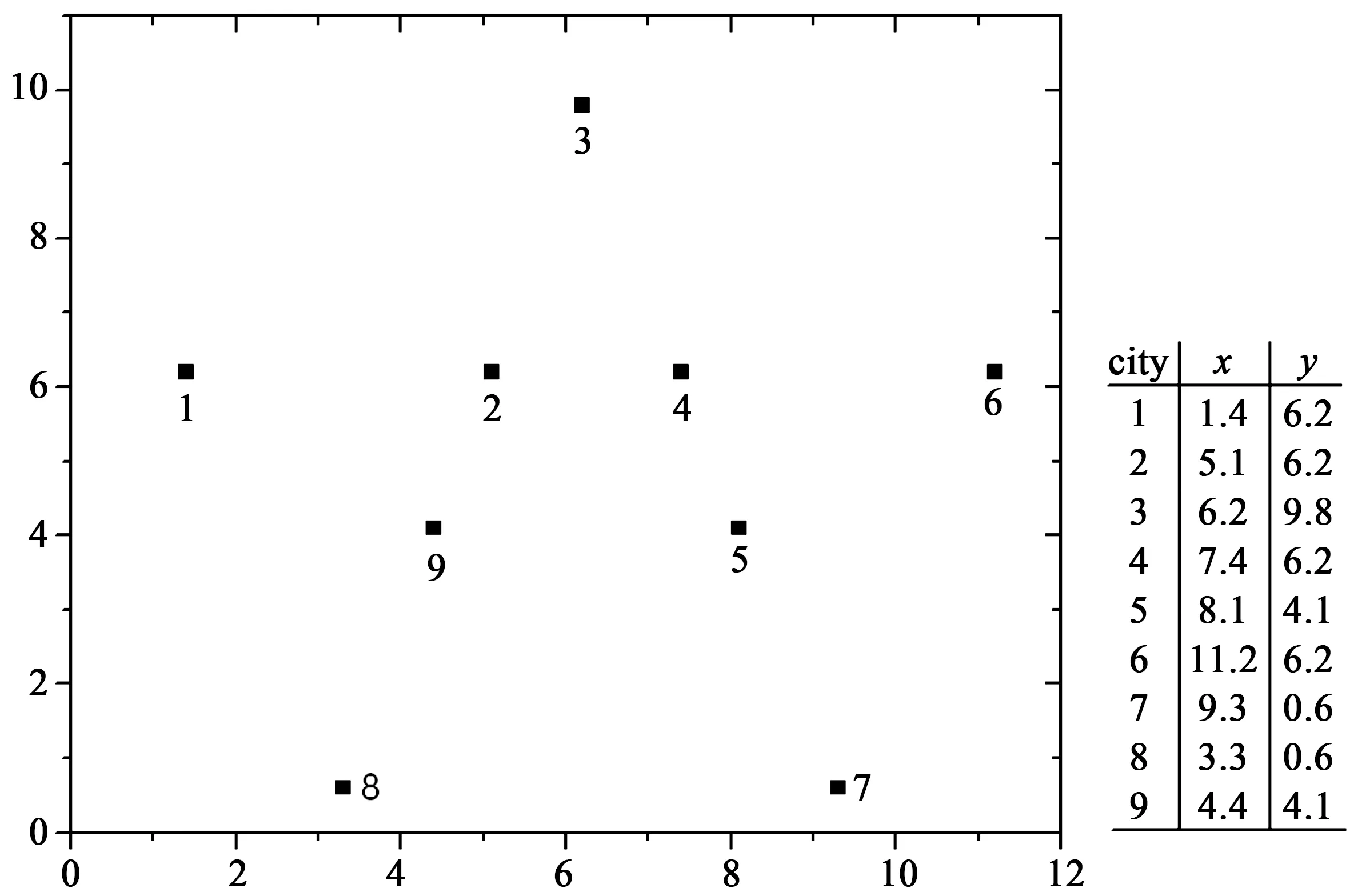
图1 9个城市的TSP问题Fig.1 A TSP problem involving nine cities

把生成子回路消除约束(10)～(13)添加到AP中，构造松弛的TSP。该松弛TSP的可行解可以避免已经出现的子回路再次出现。松弛的TSP的最优解可以生成4个新的子回路：1→9→8→1、2→3→2、4→6→4和5→7→5。此时，总的出行费用为35.773，并可以生成新的子回路消除约束如下：

x19+x98+x81≤2，

(14)

x23+x32≤1，

(15)

x46+x64≤1，

(16)

x57+x75≤1。

(17)

将约束条件(14)～(17)添加到上述松弛的TSP中，可以得到新的松弛的TSP。通过求解该松弛的TSP，我们可以得到最优解为1→2→3→4→6→5→7→8→9→1，总的出行费用为35.834。该最优解只含有一个子回路，因此也是原始TSP的最优解。

3.2 TSP库中的TSP

我们采用TSP库中的问题来验证提出的方法的有效性,采用IBM ILOG CPLEX 12.5求解LIP子问题。所有计算均在具有Intel(R)Core(TM)i5-2400 3.10GHz CPU和8GB RAM的计算机上运行。已有的研究表明，DL模型的求解速度在整体上比其他模型快[16-17]。因此，本文只对比所提出的方法和直接求解DL模型。

表1中给出的结果表明，所提出的方法和DL模型都可以得到TSP的最优解，且大多数情况下，提出的松弛方法具有更高的求解效率。通过求解一些规模较大的问题(如rbg323、rbg358)可以明显看到，本文方法比求解DL模型具有更快的求解效率,所提出的方法对求解效率的提升主要得益于子回路消除约束条件数量的减少。表1中的结果表明，所提出的方法只需要小于3n个起作用子回路消除约束。因此，对于某些TSP，有效子回路消除约束的大小是O(n)。

表1 松弛算法与DL模型求解TSP的结果对比

4 结论

本文提出了通过求解松弛的TSP来确定TSP问题的有效子回路消除约束，并基于有效子回路消除约束实现TSP的全局最优求解。所提出方法的每个松弛问题的约束规模大小可以减少到O(n)，可以大大减少TSP求解所需要的迭代次数和CUP时间。通过求解大量TSP，验证了本文方法的可行性以及求解效率。结果表明，本文提出的方法在计算效率方面明显优于直接采用Cplex求解TSP的DL模型。