车辆弯道行驶横向加速度干扰模型的研究
许伦辉,黄宝山
(1. 北京理工大学 珠海学院 工业自动化学院,广东 珠海 519088; 2. 华南理工大学 土木与交通学院,广东 广州 510640)
交通安全是交通工程研究的重要课题。车辆在道路行驶过程的安全性受道路线形、路面质量、车辆状况、气象条件、驾驶技术等众多因素影响。尽管单个交通事故具有随机性和偶然性,但基于大数据分析表明:在道路交通事故的黑点路段,往往能找到交通事故与道路线形之间的内在相关性[1]。因此,基于道路线形的车辆行车安全性研究有利于甄别和排除道路事故黑点路段,建立道路线形参数加速度干扰模型是近年来确定道路行车安全性与线形参数关系的一个重要方向[2]。
1 问题描述
车辆行驶过程中,其行驶状态处于时刻变化中,其行驶速度在一定范围内摆动。R.HERMAN等[3]首先提出了以加速度干扰描述车辆行驶速度的摆动的观点,即分析车辆加速度对平均加速度的标准差,其计算如式(1)、(2):
(1)
(2)
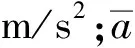
自从加速度干扰这一能定量描述车辆行驶平稳性的概念提出后,随后的研究主要围绕如何建立加速度干扰模型及加速度干扰大小与行车安全性舒适性的关系进行展开。基于式(1)一般形式,文献[4]建立了三维加速度干扰的形式化模型,将平面弯道简化为标准圆弧,并分析了道路线形圆心角、半径、车速对行车安全舒适性影响。文献[5]结合道路平面线形特点,将加速度干扰模型进行便于实际计算的离散化处理,并通过实例分析了道路平面线形加速度干扰变化特征。文献[6]从横、轴、竖3个方向给出了加速度干扰模型的具体形式。文献[7]分别建立水平、竖直方向的分加速度干扰模型,并给出了两个方向各自的权重系数,在此基础上建立了缓和道路曲线上的合加速度干扰模型,并通过实例验证分析了回旋线参数和行驶速度对加速度干扰及行车舒适性的影响。文献[8] 采用分层控制结构对巡航车辆的跟随性和安全车距控制问题研究了紧急制动工况下的舒适性和安全性。文献[9]基于高速公路交通事故的统计数据,分析了不当越线超车与交通安全的内在关联性。此外,根据大量实验数据和案例分析发现[10-12]:行车安全性与加速度干扰大小成反比。加速度干扰越小,行车安全性、舒适性能越好,反之则越差。目前学界普遍认同的观点是:当σ>1.5 m/s2时,行车安全性很差,需要进行安全预警;当σ<0.7 m/s2时,行车安全性和舒适性好;当0.7 m/s2<σ<1.5 m/s2时,车辆处于正常行驶状态。
笔者针对车辆行驶在弯道上的特定路段,基于典型的缓-圆-缓弯道建立了由弯道曲率和弯道长度描述的横向加速度干扰模型,为评价弯道路段行车安全性舒适性提供依据。
2 横向加速度计算
在道路平曲线的行驶过程中,车辆所受作用力的计算如式(3):
(3)
式中:FR为车辆所受离心力,N;G为车辆自重,N;v为行驶速度,m/s;R为行驶道路上平曲线的半径,m;g为重力加速度,g=9.8 m/s2。
受离心力影响,汽车难以稳定行驶,且有可能向侧向滑移或横向倾覆,引发行车事故。因此,在道路设计过程中会采取设计横向坡度方法以避免离心力干扰,进而提高行车安全性能[11]。在道路平曲线上车辆的受力作用情况如图1。

图1 道路平曲线上汽车受力Fig. 1 Vehicle stress on the road horizontal curve
由图1,可分解为重力与横向作用力,如式(4)~(7):
Fh=FRcosa-Gsina
(4)
Fs=FRsina+Gcosa
(5)
(6)
(7)
式中:Fh为横向力;Fs为纵向力。
将式(6)、(7)代入式(4)中,可得式(8):
(8)
根据牛顿第二定律Fh=mah,得ah=Fh/m,如式(9):
(9)
式中:ah为横向加速度,m/s2;R为平曲线半径,m;hc为曲线上某处路面横向内外路缘的高度差,m;b为平曲线上该处所在路面宽度的1/2,m。
文献[12]给出式(9)中车辆行驶速度,如式(10)~(12):
(10)
(11)
(12)
式中:v0为起点处速度,m/s;az为轴向加速度,m/s2;λ为海拔修正系数;δ为惯性力系数;D为汽车动力因子;f为滚动阻力系数;i为纵向坡度。
由此可得:一旦已知汽车行驶过程中某时刻的瞬时速度与其所在平曲线上的半径、超高,就能计算出相应的横向加速度值。在以上3个参数中,除了行驶速度须通过实测获得外,曲线半径及超高可通过设计资料得到。
弯道曲率k为平曲线半径R的倒数,其单位为m-1。对于缓-圆-缓类型的道路线形,曲线长度l与曲率k之间的关系[11]如式(13):
(13)
式中:k为曲线某线上某一点的曲率值,m-1;R为圆曲线半径,m;A1为第一缓和曲线参数;A2为第二缓和曲线参数;l为任意点的曲线长度,m;l1为第一缓和曲线长度,m;l2为圆曲线长度,m;l3为第二缓和曲线长度,m。
又有:tanα=ih=hc/b,ih为超高横坡度。则横向加速度可表示如式(14):
(14)
根据式(10)可得车辆在缓-圆-缓弯道行驶中的横向加速度,如(15)~(17):
1)第一缓和曲线,当0≤l≤l1时:
(15)
2)圆曲线,当l1≤l≤l1+l2时:
(16)
3)第二缓和曲线,当l1+l2≤l≤l1+l2+l3时:
(17)
3 建 模
在曲线上行驶过程中,车辆同时受重力和离心力,因而产生了横向加速度。车辆在弯道路段横向加速度干扰即为横向加速度对平均横向加速度的标准差,大小与行车安全性舒适性密切相关。
已知横向加速度ah为关于曲线长度l的函数,即ah=a(l),那么横向加速度干扰σ如式(18):
(18)
由此可依次得到车辆在缓-圆-缓弯道行驶中横向加速度干扰模型。
1)第一缓和曲线,当0≤l≤l1时,有式(19)~(21):
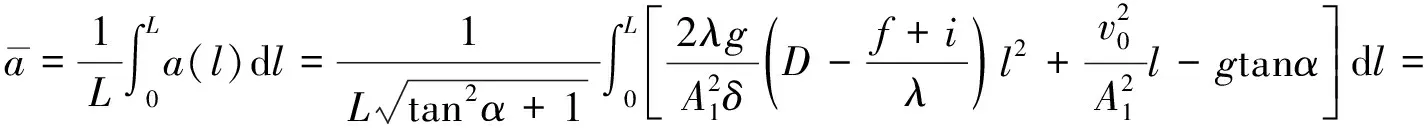
(19)
(20)
(21)
2)圆曲线,当l1≤l≤l1+l2时,有式(22)~(24):
(22)
(23)
(24)
3)第二缓和曲线,当l1+l2≤l≤l1+l2+l3时,有式(25)~(27):
(25)
(26)
(27)
上述模型中,式(21)、(24)、(27)中各参数含义如前文所述。
4 实例验证
笔者选取陕西省某一山岭重丘区的二级公路,道路区段为K37+425.423~K46+060.659段,全长为8 635.24 m,路基宽度为11 m,路面宽度为10 m,双向两车道,设计时速为40 km/h。
4.1 相关参数取值的确定
本验证分析计算横向加速度干扰需明确以下参数:行驶速度v,所选路段平曲线半径R,曲线长度L,海拔修正系数λ,动力因子D,滚动阻力系数f,惯性力系数δ,纵坡度i,超高横坡度ih。验证计算选取10个弯道路段,其参数取值如表1。
其中:动力因子D=0.06;滚动阻力系数f=0.02;惯性力系数δ=1.05;海拔修正系数λ=1;纵坡度i=3.5%;超高横坡度ih=2.5%。
本例选用车型为小客车,考虑其公路等级,设计时速40 km/h,故以v=40 km/h与四档作为运行速度初始值,之后各个路段行驶速度按照式(12)计算得出,计算结果如表2。
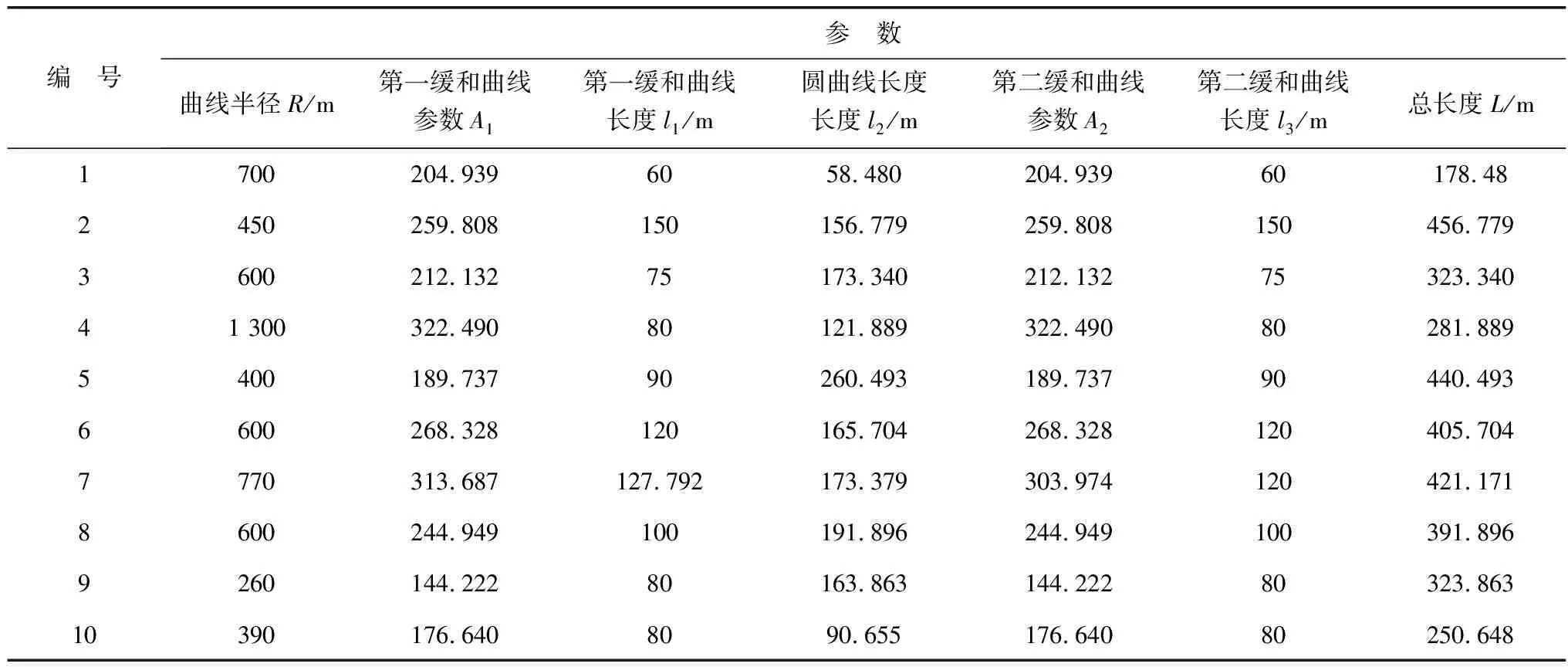
表1 所选路段的平曲线半径及曲线长度Table 1 The horizontal curve radius and curve length of the selected road section

表2 各路段车辆行驶速度计算结果Table 2 Calculation results of vehicle speed in each section (m·s-1)
4.2 横向加速度干扰计算及安全性评价
文中的计算模型可视为横向加速度干扰关于曲线长度l变化的函数。笔者在MATLAB中进行模型编程计算,进而绘制出横向加速度干扰变化曲线图,观察其曲线变化范围,以判断所在试验路段车辆行驶的舒适性与安全性。表3为实例路段行车舒适性评价结果。
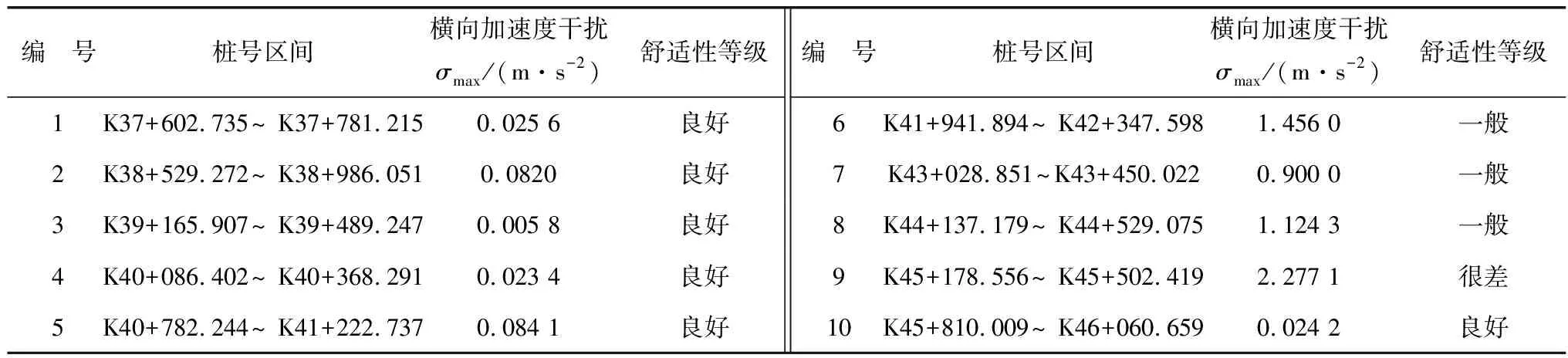
表3 测试路段车辆行驶舒适性评价结果Table 3 Vehicle driving comfort evaluation results of the tested sections
当横向加速度干扰σ>1.5 m/s2时,行车安全性很差;当0.7 m/s2<σ<1.5 m/s2时,车辆处于正常行驶状态;当σ<0.7 m/s2时,行车安全性和舒适性好。由表3可看出:该路段行车舒适性整体较好;其中:6~8号测试路段横向加速度干扰分别为4.156、0.900与1.124 3,显著大于其它路段,安全舒适性较差。影响因素包括车辆行驶速度、道路纵坡度、曲线半径及曲线长度等道路平曲线的平纵组合。6号路段主要是因为车辆行驶速度较大;7号路段行车舒适性差的原因在于其半径差值过大,从2 km变化到了0.77 km,线形顺畅性太差;9号路段曲线半径是所有测试路段的最小值,仅为0.26 km。平曲线路段车辆行驶安全舒适性由以上因素共同决定。
5 结 语
笔者从动力学角度分析了汽车的动力特性,从行驶力学角度分析了汽车在道路平曲线上的受力情况,进而明确了车辆横向加速度与弯道线形参数的关系,并依据加速度干扰理论和加速度干扰模型定义式,建立了车辆行驶在缓-圆-缓弯道路段的横向加速度干扰模型。通过某条二级山区公路的实际线形参数对所建立车辆弯道行驶横向加速度干扰模型进行验证,验证结果表明:文中给出的模型和方法能为行车安全性评价提供新的途径。

