索梁结构面内耦合振动机理研究

赵文忠，康 健，梁 栋

(1. 河北工业大学 土木与交通学院，天津 300401； 2. 河北省高速公路曲港筹建处，河北 定州 073099)

0 引 言

索因其质量轻、强度高、阻尼小的优点被广泛应用于工程结构，索梁组合体系作为斜拉桥的重要组成结构，非线性问题较为突出。鉴于现代工程轻型预制化的发展方向，主梁会在车辆或风雨等激励下出现大幅振动的现象，大柔度的斜拉索受其影响，同样发生剧烈振动，短时间使索间碰撞，部件连接失效，长时间引起拉索的保护层脱落或疲劳破坏，对斜拉桥整体安全与耐久性能十分不利。法国布鲁东纳大桥、加拿大安纳西斯大桥、美国伯灵顿大桥与阿根廷瓜渚大桥等都曾观测到外部激励与参数激励的现象[1]。

众多学者对索梁间的非线性耦合振动相关问题进行了不同程度探索。Y. FUJINO等[2]基于Gimsing观察到斜拉桥整体模态与局部模态的研究成果提出了三自由度索梁组合结构模型，同时进行了索横向振动频率、梁横向与竖向振动频率满足1∶1∶2的缩尺模型试验，观察到全局模态和局部模态线性耦合的模态失真现象；J. M. W. BROWNJOHN等[3]以全尺寸试验和分析模型研究了曲线斜拉桥的动力特性，发现上部结构的相互作用会使索产生不同的振动形式；汪至刚等[4]将索简化为弦，同时考虑桥面质量与刚度的作用，通过数值积分得到了斜拉索会与主梁在规定条件下发生参数共振的结论；在此基础上，赵跃宇等[5]建立了与实际更相近的多自由度索-悬臂梁模型，利用连接与边界条件得到索梁结构的耦合运动方程与离散化动力学方程，使用摄动方法进行非线性响应分析与共振模式的数值模拟，分析各参数变化对耦合系统的影响，并以试验的方式验证；近年来，WEI Minghai等[6]探讨了索梁耦合体系在参数激励与外部激励下的非线性响应；冯维明等[7]研究了完全参数激励下柔性拉索与弹性悬臂梁耦合结构的非线性动力学问题，得到离散的常微分方程，进而探索阻尼参数对耦合系统的影响；吴庆雄等[8]进行了单索-梁结构和双索-梁结构模型振动试验，采用斜拉桥整体动力分析有限元方法建立了索梁结构有限元模型，并推导得到了多索-梁结构固有振动的频率方程和振型函数。

上述研究大多关注单根拉索或单自由度的基本模态与索梁共振特性研究，缺乏对多根拉索高阶振动模态及其相互影响的综合考量。因此，笔者将着重分析索-梁组合结构的非线性耦合振动响应，改进索梁模型，进而探究该组合结构的耦合机理。

1 单梁多索结构动力学分析

建立如图1所示索梁模型以模拟成桥，3根索的一端与主梁耦合，另一端与固定桥塔铰接，梁的两侧铰支。分析过程中的基本假定为[9]：索的变形关系服从胡克定律且各点受力均匀；认为索的重力垂度曲线是抛物线；不计索的抗弯刚度、抗扭刚度及抗剪刚度；在弦向方向拉索只受沿索长均匀分布的自重荷载；不计桥塔振动影响。

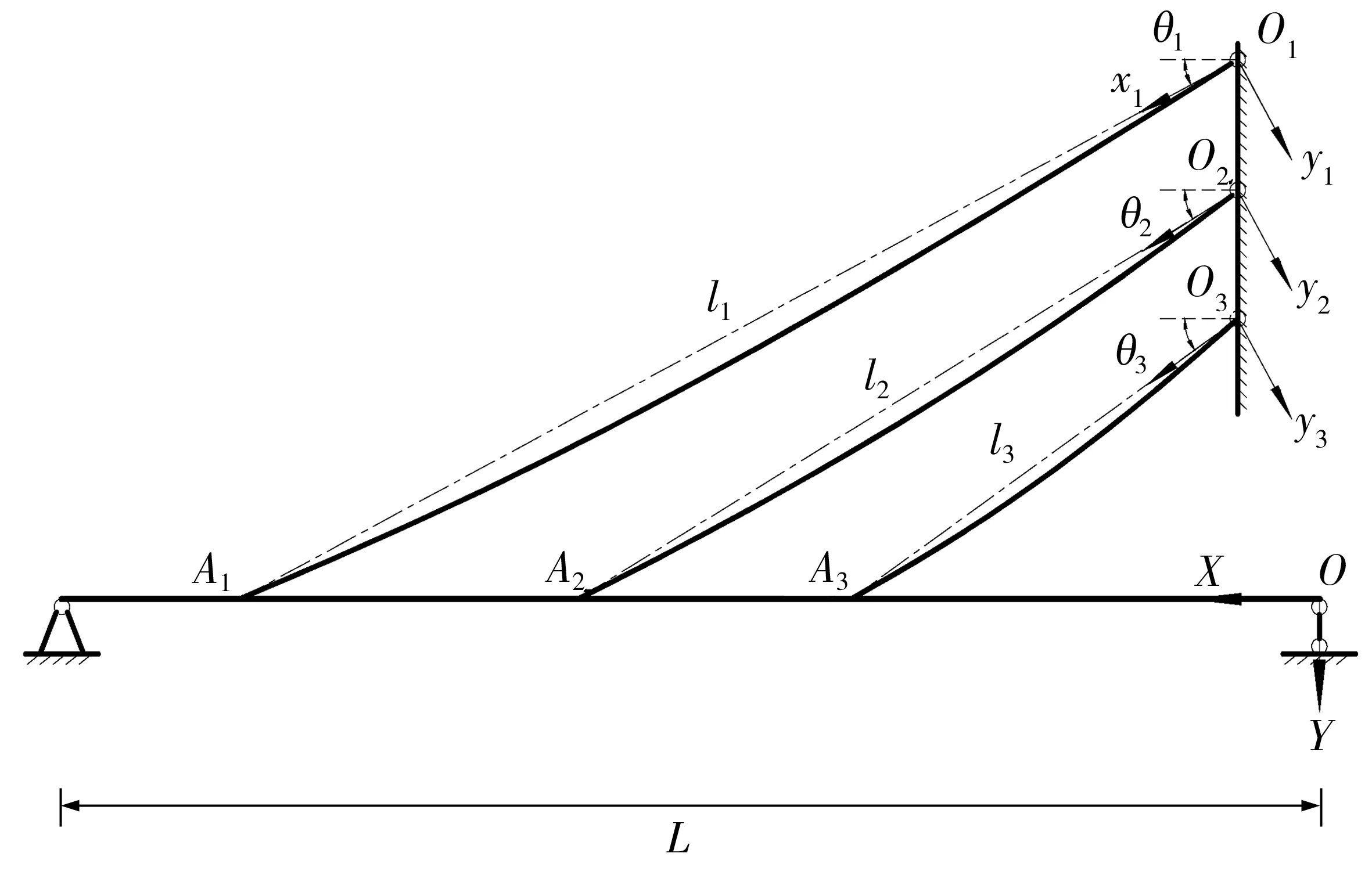
图1 斜拉桥单梁多索模型Fig. 1 Single beam multi-strip cable model of cable-stayed bridge

其中，斜拉索O1A1、O2A2与O3A3的面内运动分别由坐标系x1O1y1、x2O2y2、x3O3y3描述，主梁在竖直面内的运动以坐标系XOY描述。图中L为主梁长度，l1、l2、l3分别为索O1A1、O2A2与O3A3弦长。假设各拉索具有相同的单位长度质量m、弹性模量E、横截面面积A与阻尼系数c，根据Hamilton原理分别建立它们的面内径向运动微分方程为(3根拉索方程相似，因此不再赘述)

(1)

式中：T1为斜拉索O1A1某一振动时刻的初始轴向张力；x1、y1分别为索O1A1在平面内索弦向和径向的振动方向；v1为索O1A1在坐标系的平面内y方向振动的动位移；s1为索O1A1长度；θ1为索O1A1弦向与水平方向的夹角(忽略振动时的角度变化)。

代入轴向与弦向张力关系、重力平衡关系可将式(1)表示为

(2)

式中：H11中的H为与轴向张力T对应的弦向张力，第1个角标1为索O1A1，第2个角标1为构成索轴向张力的静张力， 2为构成索轴向张力的由斜拉索振动引起的动拉力， 3为构成索轴向张力的由主梁竖向位移引起的动拉力。

斜拉索拉力部分表示为

(3)

式中：f1为索O1A1的垂度；V1为索O1A1与主梁结合处梁的振动位移。

由于斜拉桥中索的质量远小于主梁的质量，为进一步简化，不考虑拉索振动对主梁振动的影响，把索对主梁的作用等效为施加于主梁上的弹性支撑和一个轴向压力[10]。

图2 弹性支撑简支梁Fig. 2 Simply supported beam with elastic support

图2中，K是索对梁作用的弹簧刚度，K1=EAsin2θ1/l1，K2=EAsin2θ2/l2，K3=EAsin2θ3/l3。

根据Hamilton原理，双索梁模型中梁的运动微分方程为

(4)

式中：M为梁沿水平方向分布的每延米质量；cb为梁的阻尼系数；EbIb为梁的抗弯刚度。

综合式(2)～式(4)即为索梁耦合振动的运动微分方程。

索梁连接处的变形协调条件为

(5)

体系的边界条件为

(6)

2 单梁多索结构离散分析

为了简化主梁与斜拉索的振型曲线，将主梁竖向、索径向与面外的振动模态进行变量分离。根据体系边界条件假设主梁的振动模态为[11]

(7)

根据索梁连接处位移一致的原则，同时考虑二阶模态对耦合振动的影响，索O1A1、O2A2与O3A3面内径向的振动模态可设为

(8)

(9)

(10)

忽略结构阻尼，对体系进行Galerkin离散分析，可以得到振动方程为

(11)

式中：

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

通过式(11)可以看出，在斜拉索与主梁振动方程中均包含有线性项、二次项与三次项，这表明结构存在非线性振动。在忽略阻尼而考虑垂度的情况下，单根斜拉索的振动与其垂度、面内振动、一二阶模态、主梁振动等参数均有关，而多根斜拉索也经由梁间接地联系在一起。将通过合理控制工况条件进行数值模拟，以探究该组合体系耦合振动过程中的索梁响应与影响原理。

3 数值模拟

参考现行规范并结合实际工程，拟定斜拉索O1A1、O2A2与O3A3基本参数为：E=1.95×1011Pa，l1=260 m，l2=225 m，l3=200 m，A=0.001 2 m2，f1=1.2 m，f2=1.1 m，f3=1 m，θ1=28°，θ2=32°，θ3=35°，m=100.8 kg/m，T11=6.5×106N，T21=4.86×106N，T31=3.82×106N；主梁的基本参数为：Ib=8.5 m4，Eb=7.5×109Pa，M=1×105kg/m，L=300 m，L1=260 m，L2=217.12 m，L3=190.14 m。

既有研究表明[12]，当主梁振动频率与索面内一阶固有频率相同时二者会谐波振动，由此确定文中频率比：索O1A1面内一阶固有频率ω1、索O2A2一阶频率ω3、索O3A3一阶频率ω5与主梁固有频率ω7相等，索O1A1面内二阶频率ω2、索O2A2二阶频率ω4与索O3A3二阶频率ω6均为其二倍。假设了5种初速度均为0而初始激励不同的振动工况，如表1。

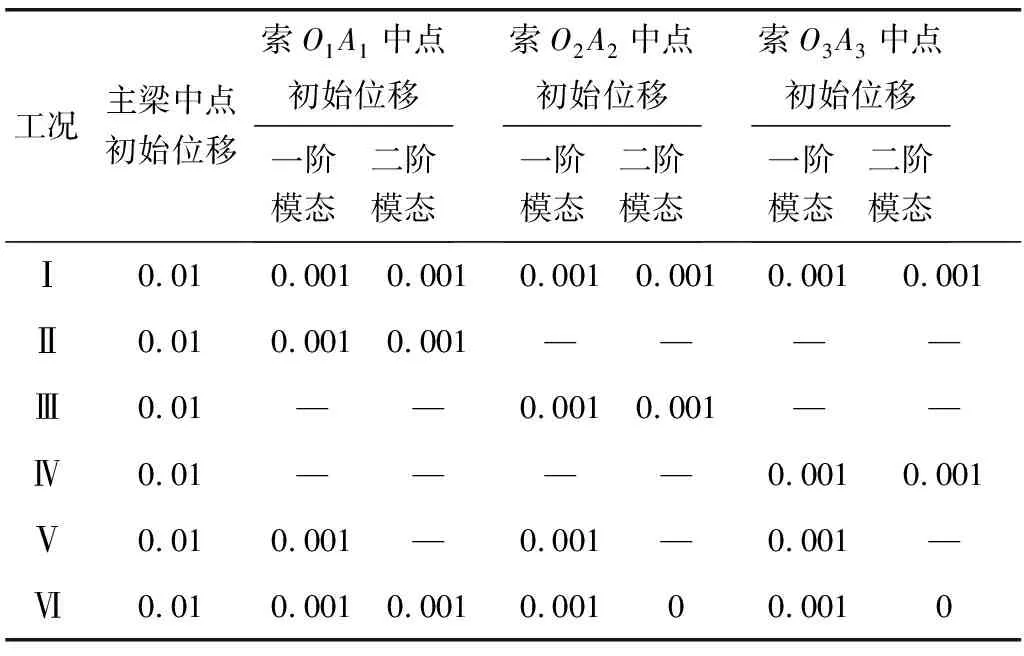
表1 索梁振动工况Table 1 Working condition of cable-beam vibration m

将以上参数代入离散后的振动方程，通过四阶-五阶Runge-Kutta法，得到不同工况下体系无阻尼振动时的时间位移曲线，结果如图3～图13。

图3 索O1A1中点一阶时程曲线(Ⅰ)Fig. 3 First-order time-history curve at the midpoint of cableO1A1(Ⅰ)

图4 索O1A1与梁结合处梁的时程曲线(Ⅰ)Fig. 4 Time-history curve of beam at the junction of cable O1A1and beam(Ⅰ)

图5 索O1A1中点二阶时程曲线(Ⅰ)Fig. 5 Second-order time-history curve at the midpoint of cableO1A1(Ⅰ)

图6 索O2A2中点一阶时程曲线(Ⅰ)Fig. 6 First-order time-history curve at the midpoint of cableO2A2(Ⅰ)

图7 索O3A3中点一阶时程曲线(Ⅰ)Fig. 7 First-order time-history curve at the midpoint of cableO3A3(Ⅰ)

图8 主梁不同初始扰动下索O1A1跨中一阶模态最大振幅Fig. 8 First-order maximum amplitude at the midpoint of cableO1A1 with different initial disturbance of beam

图3、图6与图7分别表示梁中点的初始位移为0.01 m、索面内受到初始扰动为0.001 m且初始速度均为0时索O1A1、O2A2与O3A3中点一阶振动模态时程曲线。图4、图5分别为同样工况下对应索梁结合处梁的时间位移曲线与索O1A1中点二阶振动模态时程曲线(各索梁连接处梁的时程曲线、各索二阶时程曲线均类似)。图8为工况I条件下改变主梁初始位移，对应索O1A1跨中一阶模态振动最大振幅。在工况I的振动过程中，索的一阶模态振动位移由初位移开始同步周期性地增大、减小，而索的二阶位移和梁的位移也存在相似现象，由最初位移周期变化，且短时间内最大振幅变化不明显。不同的是，斜拉索一阶模态与主梁振动均为同步增减，而相应二阶模态正负方向最大振幅交叉呈现。在频率满足条件的情况下，当两条索面内一阶模态位移减小时，对应时刻梁的位移增大，振幅周期性地“互补”，表明梁与索一阶模态存在能量交换，即为明显耦合现象。索二阶模态正方向的最大振幅对应负方向的最小振幅，与索一阶最大振幅、梁的最小振幅同时出现，且“拍”频是它们的二倍，说明索二阶模态与一阶模态、主梁振动的耦合程度不高。由于结构频率比不同，索的一阶模态振动与主梁发生谐波共振，二阶模态与主梁发生超谐共振现象。因为索一阶模态在主梁不同初始挠度下出现超过初位移100倍的大幅振动，在主梁位移为0.55 m附近还发生了“跳跃”现象，表现为不稳定的非线性，而二阶模态的最大振幅仅为初挠度的二倍左右，因此在小扰动与特定频率条件下，索梁耦合振动中主要考虑一阶模态是合理的。

图9、图10与图11表示梁中点的初始位移为0.01 m、索面内受到初始扰动为0.001 m且初始速度均为0时索O1A1、O2A2与O3A3分别单独与主梁耦合情况下索中点一阶振动模态的时程曲线。表2为前4种工况下拉索面内一阶模态的最大振幅。类似多索单梁的耦合关系，单索单梁的耦合振动也存在周期性地变化，但索的面内一阶模态振幅较三索耦合有明显降低，降幅达97%，且“拍”频加快，三者比较，振幅变化幅度愈显著，变化速率愈缓慢，表示在多索结构中，某根拉索的大幅振动可能是由附近或更远处的索导致的，同时，单根索的能量也会通过主梁传递给其他拉索，以振幅与频率变化的形式表现出来。因此，大跨度斜拉桥的拉索间并不孤立，而是通过与主梁的耦合振动连接成一个整体。还应该注意到的是，对于三索与梁耦合振动的情况，索O2A2面内一阶振幅最大，索O1A1振幅最小，这是由于索O1A1、O2A2与O3A3在与主梁结合处受到的激励依次增大，而初始弦向张力依次减小。这也表明拉索振幅不一定与拉索长度成比例，处于梁段中部的索振幅有可能最大，对于实际斜拉桥还应综合考虑环境激励等其他因素。

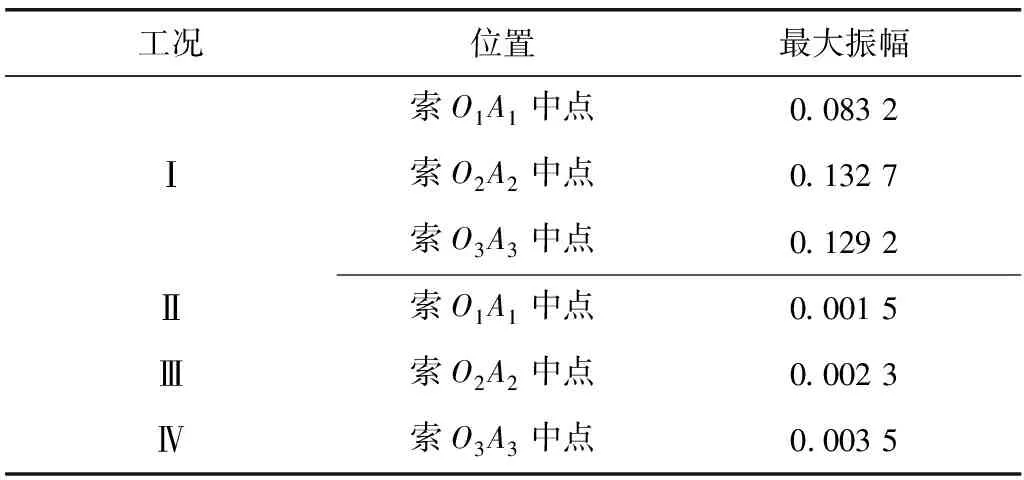
表2 不同工况下拉索一阶模态最大振幅Table 2 First-order maximum amplitude of cable under differentworking conditions

图9 索O1A1中点一阶时程曲线(Ⅱ)Fig. 9 First-order time-history curve at the midpoint of cableO1A1(Ⅱ)

图10 索O2A2中点一阶时程曲线(Ⅲ)Fig. 10 First-order time-history curve at the midpoint of cableO2A2(Ⅲ)

图11 索O3A3中点一阶时程曲线(Ⅳ)Fig. 11 First-order time-history curve at the midpoint of cableO3A3(Ⅳ)

图12为不考虑拉索二阶模态振动情况下，梁中点的初始位移为0.01 m、索面内一阶模态受到初始扰动为0.001 m且初始速度均为0时索O1A1中点面内一阶模态振动的时程曲线。图13为类似工况下考虑拉索二阶模态，但索O1A1二阶模态初始位移为0.001 m，其余索二阶模态没有受到初始扰动时索O1A1中点一阶模态的时程曲线。经对比可以看出，在相同的时间内，考虑二阶振动模态的拉索周期性的最大振幅无明显变化，2 000 s左右的最大振幅为0.816 3 m，而没有考虑二阶模态的拉索一阶模态振幅却出现减小趋势，同一时刻的最大振幅为0.700 9 m。由此可见，二阶模态振动对持续性的索梁耦合振动有显著影响，拉索长时间的大幅振动有可能造成其疲劳破坏，因此，在进行拉索疲劳性破坏研究时应将二阶模态纳入考量。

图12 索O1A1中点一阶时程曲线(Ⅴ)Fig. 12 First-order time-history curve at the midpoint of cableO1A1(Ⅴ)

图13 索O1A1中点一阶时程曲线(Ⅵ)Fig. 13 First-order time-history curve at the midpoint of cableO1A1(Ⅵ)

4 结 论

在忽略系统阻尼而考虑垂度的条件下建立了单梁多索结构面内运动微分方程与非线性离散方程，重点探讨了在特定频率条件下主梁和3根斜拉索以及索面内一、二阶模态间的耦合振动关系，得到以下结论：

1)在单梁多索组合体系中，索与梁、索面内一阶与二阶模态振动互相影响，当索面内一阶模态固有振动频率与主梁相同，二阶模态频率为其二倍时，受扰动均会发生不同程度耦合振动现象。与单梁单索结构相比，三索耦合时的振幅与拍频明显不同，表示索与索之间存在能量传递，这种耦合作用将多根索通过主梁间接联系在一起。对类似多索结构而言，索间作用不可忽视。

2)索梁耦合振动过程中，拉索一阶模态出现远超初始扰动100倍以上的大幅振动，同时表现出不稳定的非线性特征，对结构安全造成威胁。

3)索二阶模态耦合振动的最大振幅仅为初始扰动的二倍，在小扰动条件下可以忽略其短时影响。但由于二阶模态振动会造成耦合中的索持续大幅振动，因此研究拉索疲劳问题时应考虑其作用。