基于协方差矩阵特征向量的圆环阵目标方位估计方法

朱少豪, 杨益新, 汪 勇

基于协方差矩阵特征向量的圆环阵目标方位估计方法

朱少豪, 杨益新, 汪 勇

(西北工业大学 航海学院, 陕西 西安, 710072)

为解决传统高分辨方位估计(DOA)算法计算量大、不稳健的问题, 文章首先利用圆环阵空间均匀噪声场中噪声协方差矩阵的特征向量重新定义了不同阶数的特征向量和阵列流形向量, 并将数据采样协方差矩阵根据阶数的大小进行了降维处理, 最后利用新的阵列流形向量和降维的数据采样协方差矩阵采用最小方差无失真响应(MVDR)进行目标方位估计。仿真结果表明, 在没有误差的情况下, 所提方法的最高阶方位估计结果与传统MVDR一致; 存在幅度和相位误差时, 更稳健的低阶方位估计的结果要优于传统MVDR方法, 在提升了抗误差稳健性的同时, 降维的数据协方差矩阵也大大减少了求逆的计算量。海试结果验证了文中方法的有效性, 采用的12元均匀圆环阵, 其2阶和3阶方位估计的结果要优于传统的MVDR方法。文中方法可为水下无人系统等平台上的圆环阵水下目标方位估计提供应用参考。

水下无人系统; 圆环阵; 特征向量; 协方差矩阵; 方位估计; 最小方差无失真响应

0 引言

在水下无人系统、声呐系统以及空气中的智能音箱等工作平台上, 常常需要声传感器阵列采用波束形成完成信号降噪、目标识别和方位估计等任务[1-3]。由于平台空间有限, 声传感器阵列的尺寸需要加以限制, 但是传统的常规波束形成方法由于受到瑞利准则的限制, 在低频时需要较大的尺寸才能有较高的角度分辨率进行目标方位估计, 这在实际应用中往往难以实现。

几十年来, 针对常规波束形成分辨率低的问题, 人们提出了很多高分辨方位估计方法。Capon[4]提出的最小方差无失真响应(minimum variance distortionless response, MVDR)方位估计是多年来常用的一种方法, 但它需要对阵列噪声采样数据的协方差矩阵求逆, 当阵元数较多时, 此方法不仅计算量会大大增加, 且容易出现奇异矩阵, 因此不是一个稳健的处理过程, 在实际应用中有时难以达到理想效果。另外, 信号子空间类法(如多重信号分类(multiple signal classification, MUSIC)[5]方法)利用了信号子空间和噪声子空间的正交性, 但其需要预知信源数量, 并且是一种非线性方法, 估计结果的峰值不等于信号的功率, 在处理过程中使用了全部的噪声特征向量, 也会导致较大的计算量。近十年, 稀疏信号处理类[6-7]方法得到广泛的关注和研究, 然而此类方法约束复杂, 并且循环迭代计算量过大, 因此实际应用还存在一定的困难。

为解决上述算法计算量大、不稳健的问题, 文中首先利用空间均匀噪声场中圆环阵噪声协方差矩阵的特征向量得到了新的阵列流形向量, 并重新定义了不同阶数的阵列流形向量和特征向量, 然后将数据采样协方差矩阵根据不同阶数的大小进行降维处理, 最后利用新的阵列流形和降维的数据协方差矩阵采用MVDR方法进行目标方位估计。理论仿真结果表明, 在没有误差的情况下, 最高阶的方位估计结果与传统MVDR方法一致; 存在幅度和相位误差时, 更稳健的低阶方位估计结果要优于传统MVDR方法。文中方法不仅提升了抗误差的稳健性, 也大大减少了矩阵求逆的计算量。海上试验结果也验证了文中方法的有效性。

1 基本信号模型

假设1个半径为, 均匀分布有个阵元的圆环阵, 如图1所示。

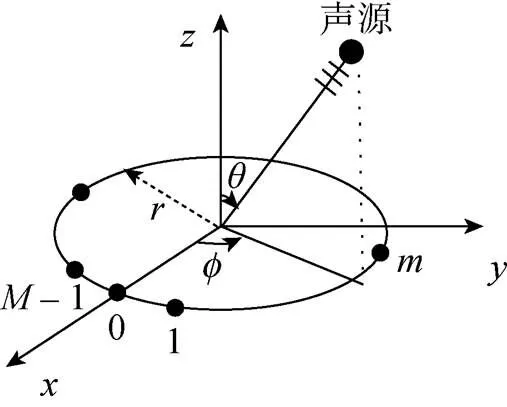
图1 圆环阵坐标示意图

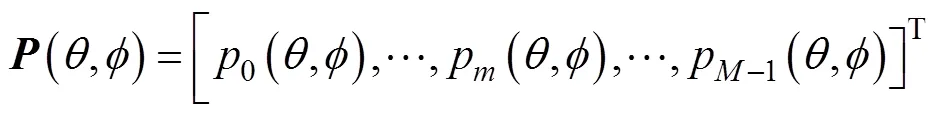
令为加权向量, 波束响应一般可定义为

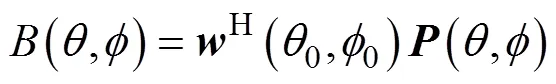
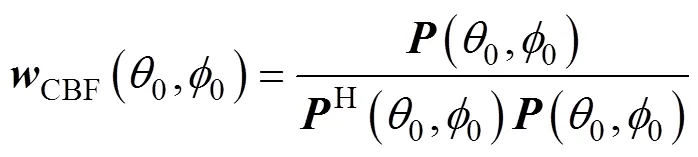
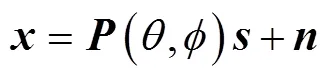
其中,是与信号不相关的随机噪声, 则阵列接收数据的采样协方差矩阵为

波束形成器方位估计的输出功率可表达为

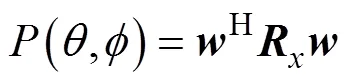
2 高阶超指向性模型

2.1 重新定义阵列流形向量

在空间均匀噪声场中, 圆环阵的噪声协方差矩阵是一个循环矩阵, 具有如下形式[9]

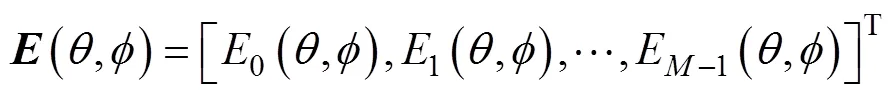
其中

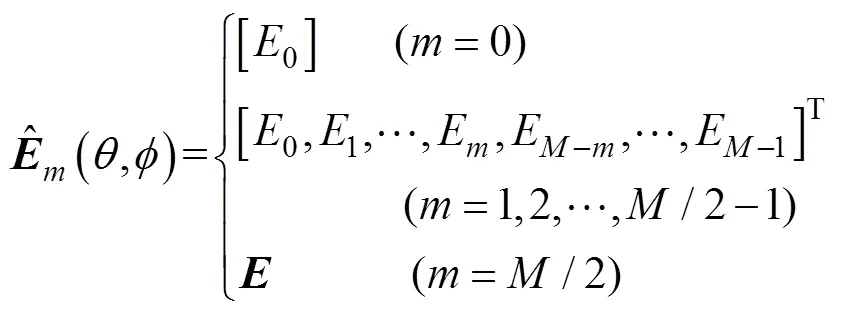
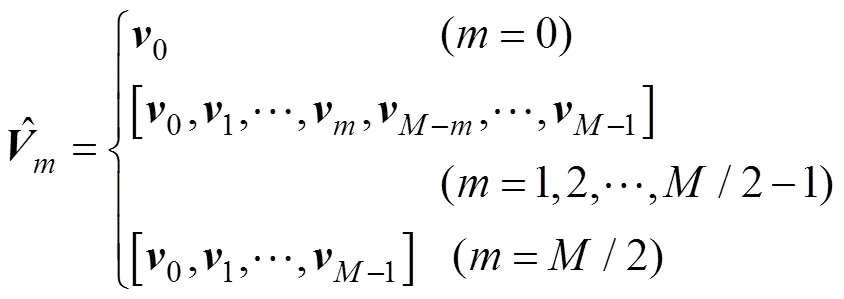
其中, 阵元数为偶数。当为奇数时, 相应的第阶阵列流形向量和特征向量可定义为

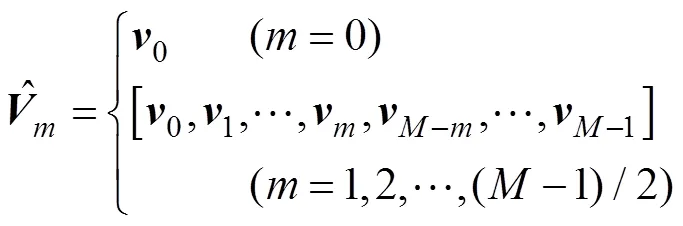
2.2 数据采样协方差矩阵

因此, 阶数越小, 矩阵的维度越小, 从而实现矩阵的降维。

2.3 MVDR方位估计

对于传统MVDR波束形成, 其最小化接收数据输出的无失真响应约束为

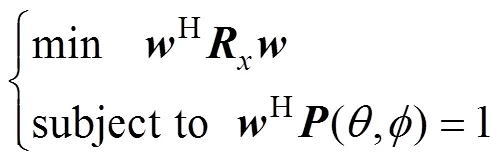
由此可得MVDR波束形成的最优加权为

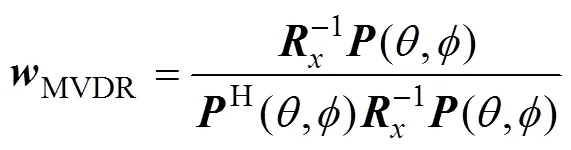
其方位估计的输出可表示为

参照MVDR波束形成, 第阶最小方差无失真响应波束形成的约束为

由此可得第阶最优加权的表达式为

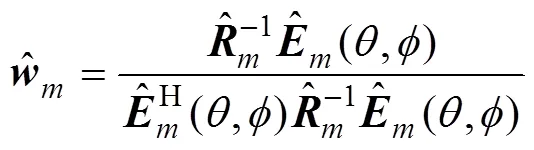
对应的第阶方位估计为

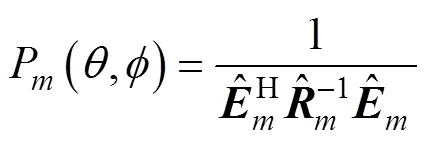
为方便后文比较, 文中提出的方法可称为特征向量最小方差无失真相应(eigenvector MVDR, EVMVDR)法。

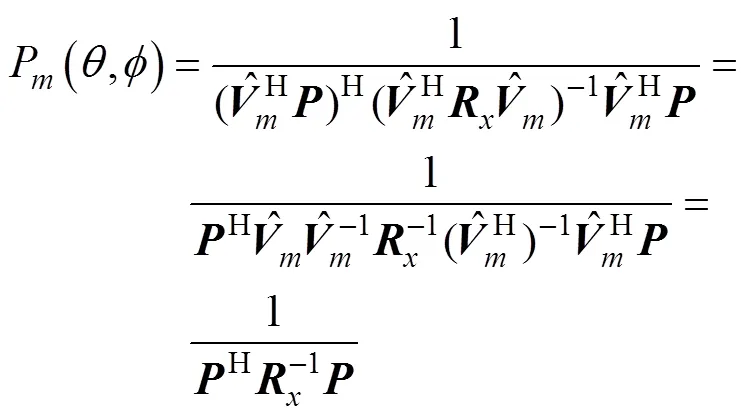
可见, 从理论上讲, 在没有误差时, 最高阶数的EVMVDR方位估计结果与传统MVDR方法一致。

2.4 误差存在时的方位估计

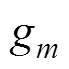
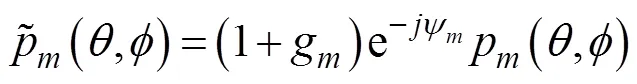
在误差存在的情况下, 阵列接收数据变为

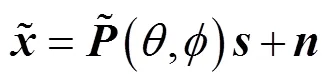
此时接收数据的采样协方差矩阵变为

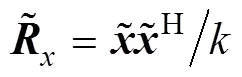
那么第阶接收数据的协方差矩阵可表示为

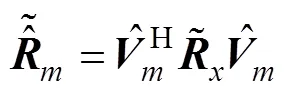
在误差存在时, 第阶基于MVDR方法的方位谱可表示为

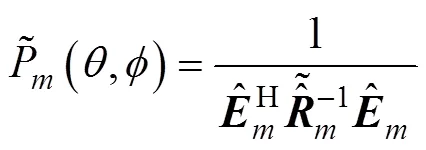
2.5 计算复杂度

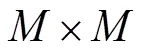
3 仿真分析

仿真中选取的圆环阵半径为= 0.5 m, 均匀分布有=12个阵元, 水下声速设为1 500 m/s, 信号采样率为20 kHz。

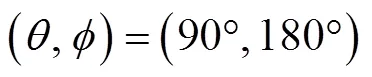
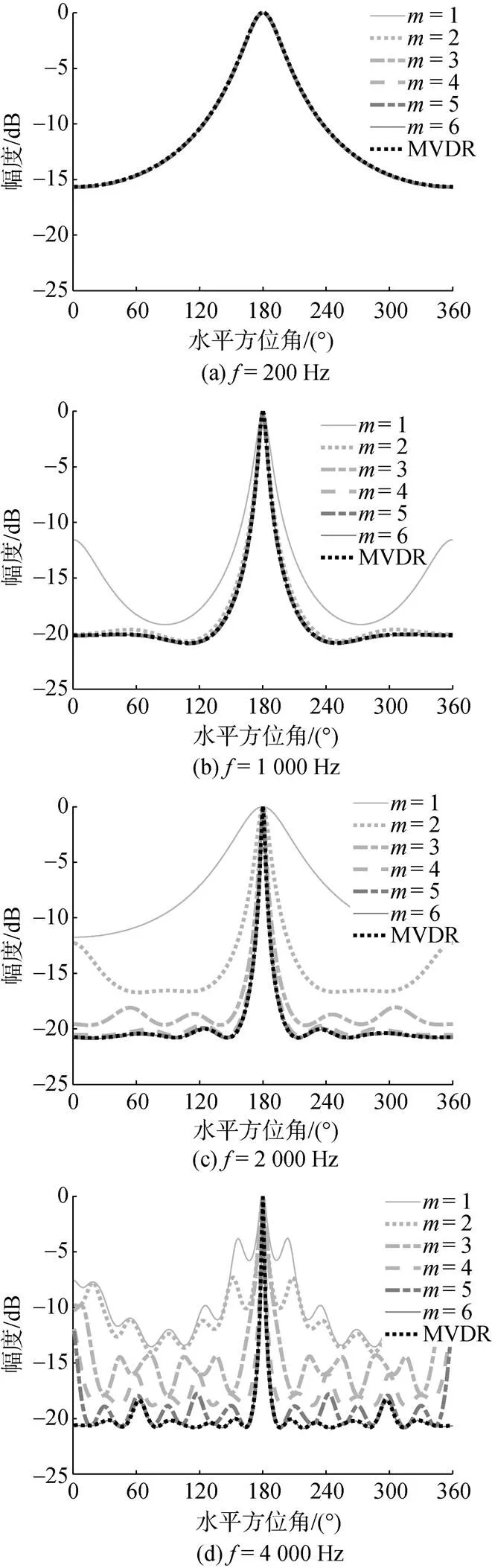
图2 特征向量最小方差无失真响应各阶方位估计和传统MVDR方位估计在不同信号频率下的对比曲线

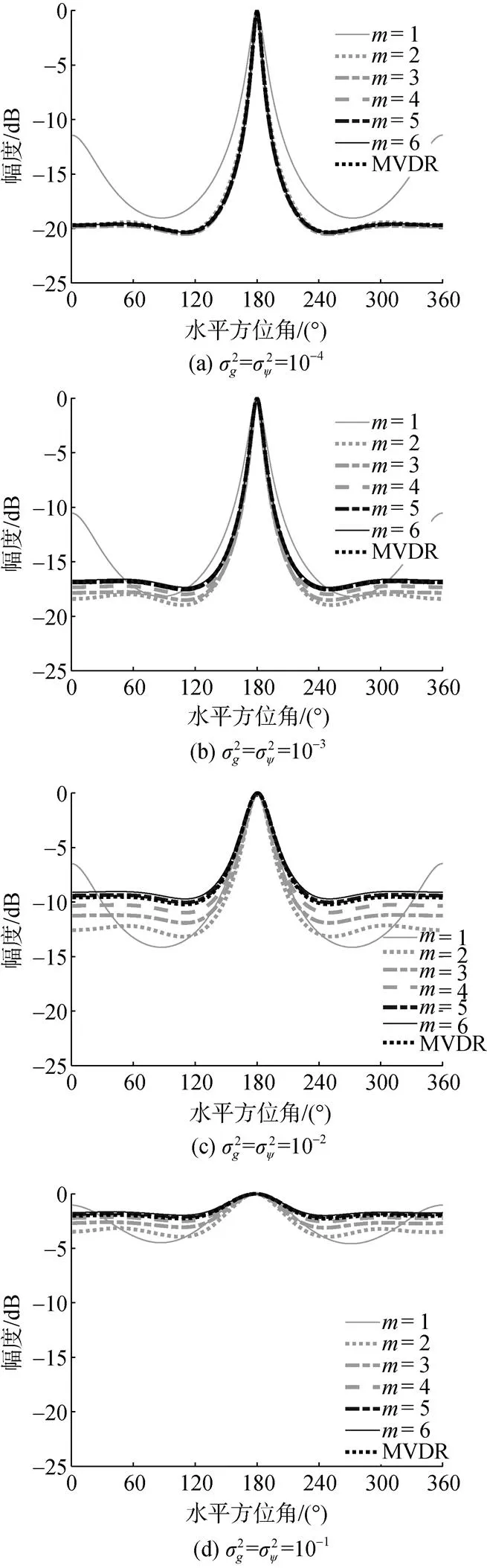
图3 圆环阵EVMVDR各阶方位估计和传统MVDR方位估计在不同幅度和相位误差下的对比曲线(f=1000 Hz)

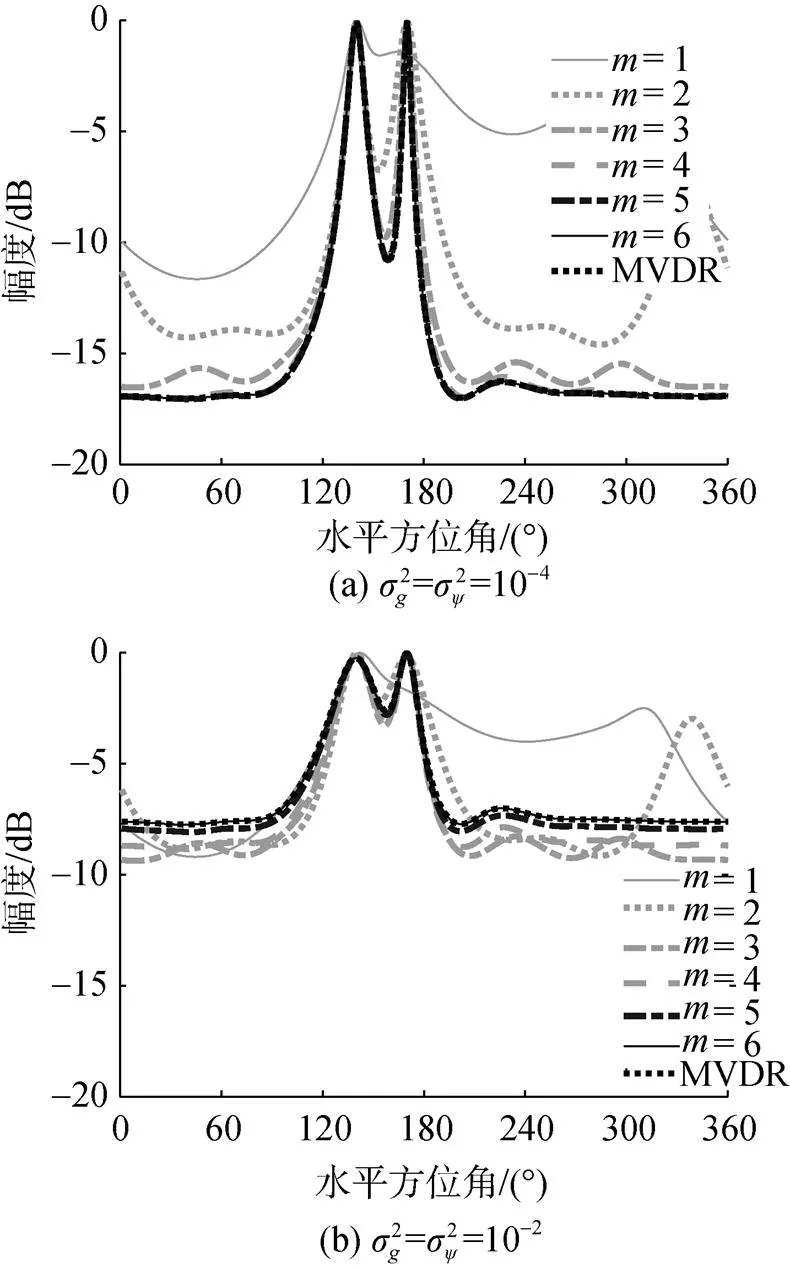
图4 存在2个目标时EVMVDR各阶方位估计和传统MVDR方位估计对比曲线

从以上仿真可以看出, 当存在一定的幅度和相位误差时, EVMVDR较低阶(如2阶和3阶)的方位估计效果要优于其高阶和传统MVDR方法, 并且低阶的噪声协方差矩阵的维度更低, 计算量更小, 适合在实际工作系统中应用。

由于俯仰维的EVMVDR方法的性能随阶数和频率的变化与水平维的性能变化基本一致, 所以仿真中只给出了圆环阵水平方向的性能, 限于篇幅, 不再给出俯仰方向的方位谱图。

4 试验验证

海试采用1个12元均匀圆环阵浮标, 半径0.5 m, 声源从远场发出的信号频率1000 Hz, 圆环阵采样率25 kHz。图5给出了EVMVDR方法中较好的2阶和3阶方位估计结果与传统MVDR方法的对比。从图5中可以看出, EVMVDR方法2阶和3阶的方位谱在主瓣宽度和旁瓣高度等性能指标上要优于传统MVDR方法。

图5 EVMVDR 2阶和3阶方位估计与传统MVDR方位估计海试结果对比曲线

实际海洋环境中的噪声复杂, 阵列随水流摇摆俯仰的角度也时刻改变, 因此接收信号复杂多变, 幅度和相位误差也不稳定, 导致各种方法方位估计的结果也不尽相同。在此次试验中, EVMVDR其他高阶方位估计的结果比2阶和3阶要差, 这也与仿真中图3的结果相吻合。

5 结束语

文中研究了一种利用空间均匀噪声场中噪声协方差矩阵的特征向量重新定义阵列流形和对数据采样协方差矩阵降维后进行目标方位估计的方法, 在一定程度上解决了传统高分辨方位估计算法计算量大、不稳健的问题。理论仿真结果说明, 在没有误差的情况下, 文中提出方法的最高阶方位估计结果与传统MVDR一致; 存在幅度和相位误差时, 更稳健的低阶方位估计结果要优于传统MVDR方法。文中提出的方法既提升了抗误差的稳健性, 也大大减少了矩阵求逆的计算量。海试结果表明, 文中所提方法的2阶和3阶方位估计结果均优于传统的MVDR方法, 与仿真结果基本一致, 从而验证了文中方法的有效性。对于阵元数较多的圆环阵, 后续将针对实际应用问题, 对EVMVDR方位估计的阶数选择做进一步研究。实际上, 文中方法同样适合其他需要数据协方差矩阵的高分辨方位估计方法。因此, 文中方法对实际水下系统中圆环阵目标方位估计具有潜在的应用价值。

[1] Stojanovic M. High-speed Underwater Acoustic Communications[M]. U.S.: Springer, 2002: 1-35.

[2] 万声国. 基于语音识别的智能WIFI音箱[D]. 南京: 东南大学, 2017.

[3] 汪勇, 杨益新, 马远良. 圆环形声学传感器阵列超指向性理论及方法[J]. 水下无人系统学报, 2017, 25(4): 297- 310.Wang Yong, Yang Yi-xin, Ma Yuan-liang. Discussion about the Superdirective Beamforming Theory and Me- thods of Circular Acoustic Sensor Arrays[J]. Journal of Unmanned Undersea Systems, 2017, 25(4): 297-310.

[4] Capon J. High-Resolution Frequency-Wavenumber SpectrumAnalysis[J]Proceedings of the IEEE, 1969, 57(8): 1408- 1418.

[5] Schmidt R O. A Signal Subspace Approach to Multiple Emitter Location Spectral Estimation[D]. U.S: Stanford University, 1981.

[6] Yardibi T, Li J, Stoica P, et al. Sparsity Constrained Deconvolution Approaches for Acoustic Source Mapping[J]. Journal of the Acoustical Society of America, 2008, 123(5): 2631-2642.

[7] 杨龙, 杨益新, 汪勇, 等. 一种改进的稀疏近似最小方差DOA估计算法研究[J]. 声学学报, 2016, 41(4): 465-476.Yang Long, Yang Yi-xin, Wang Yong, et al. Direction- of-arrival estimation of a modified sparse asymptotic minimum variance approach[J]. Acta Acustica, 2016, 41(4): 465-476.

[8] Trees V, Harry L. Optimum Array Processing : Part IV of Detection, Estimation and Modulation Theory[M]. New York, U.S.: Wiley, 2002.

[9] Ma Y L, Yang Y X, He Z Y, et al. Theoretical and Practical Solutions for High-Order Superdirectivity of Circular Sensor Arrays[J]. Industrial Electronics, IEEE Transac- tions on, 2013, 60(1): 203-209.

[10] Tee G J. Eigenvectors of Compound-Circulant and Alternating Circulant Matrices[J]. Department of Mathematics the University of Auckland New Zealand, 2005, 36(6): 195-211.

Direction-of-Arrival Estimation Using Eigenvectors of Covariance Matrix of Circular Array

ZHU Shao-hao, YANG Yi-xin, WANG Yong

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

To solve the problem that the traditional high-resolution direction-of-arrival(DOA) estimation algorithms have a large amount of computation and are not robust,the eigenvectors of noise covariance matrix of a circular array in isotropic noise field are used to redefine the eigenvectors and array manifold vectors with different orders, and the data sampling covariance matrix is reduced in dimension according to the orders. Then, DOA estimation is performed using the minimum variance distortionless response(MVDR) with the new array manifold vectors and dimension-reduced data sampling covariance matrix. Simulation results show that if there is no error, the highest-order DOA estimation result is consistent with that of the traditional MVDR method. When amplitude and phase errors exist, the more robust low-order DOA estimation results are better than that of the traditional MVDR method, which indicates that the proposed method improves the anti-error robustness, and greatly reduces the amount of computation of matrix inversion. A 12-element uniform circular array is used in the experiment conducted in the sea trail, and the results of the 2nd- and 3rd-order DOA estimation are better than that of the traditional MVDR method, verifying the effectiveness of the proposed method. This DOA estimation method may contribute to applications of circular arrays to unmanned undersea systems.

unmanned undersea system; circular array; eigenvector; covariance matrix; direction-of-arrival(DOA) estimation; minimum variance distortionless response(MVDR)

TJ630; TB566

A

2096-3920(2019)04-0379-07

10.11993/j.issn.2096-3920.2019.04.003

朱少豪, 杨益新, 汪勇. 基于协方差矩阵特征向量的圆环阵目标方位估计方法[J]. 水下无人系统学报, 2019, 27(4): 379-385.

2018-12-13;

2019-02-21.

国家重点研发计划项目(2016YFC1400200)、国家自然科学基金项目(11604259, 11527809)资助.

朱少豪(1989-), 男, 在读博士, 主要研究方向为水声信号处理技术.

(责任编辑: 陈 曦)