潜伏式武器水下施放后纵平面运动仿真

练永庆, 宋保维, 李宗吉

潜伏式武器水下施放后纵平面运动仿真

练永庆1,2, 宋保维1, 李宗吉2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2．海军工程大学 兵器工程学院, 湖北 武汉, 430033)

为了研究潜伏式武器自潜艇外部施放后在纵平面内的运动规律以及使用分离减速方案实现安全坐底的可行性, 将武器施放后的运动过程分为2个阶段, 第1阶段为武器下沉直至分离前, 第2阶段为武器分离开始直至武器完全坐底。针对这2个不同的运动阶段分别推导了相关数学模型, 并进行了整个运动过程的仿真计算, 分析了潜伏式武器水下施放后初始阶段的运动特性, 得出了分离减速坐底的规律。仿真结果证明了潜伏式武器采用分离减速方案可安全坐底。

潜伏式武器; 分离减速; 纵平面运动

0 引言

近年来, 随着海上斗争区域逐渐转向深海, 深海潜伏式武器[1-3]将逐渐登上战场。潜伏式武器一般以无动力水下航行器为载体, 通过水上或水下平台施放后, 依靠自身负浮力向海底运动直至坐底潜伏, 其后再等待时机上浮攻击水面或水下目标。在潜伏式武器总体论证研究中, 武器施放后的水下运动规律是其所关注的重点之一。目前有关水下航行器水下运动方面的研究很多[4-7], 但在类似潜伏式武器的大深度无动力航行器的下潜/上浮运动建模与仿真方面, 目前国内仅见刘正元等针对“蛟龙”号载人潜水器的无动力下潜/上浮运动所进行的研究[8-9]。文中在分析潜伏式武器被潜艇等水下平台外部施放后的运动过程基础上, 建立其水下纵平面运动数学模型, 其中包含武器在接近海底时采用分离减速方案后的运动数学模型, 并开展仿真研究, 以此来探讨潜伏式武器水下施放后在纵平面内的运动规律及其使用分离减速方案实现安全坐底的可行性, 从而为潜伏式武器的总体方案设计和论证提供理论依据。

1 潜伏式武器水下施放后运动过程

文中研究的潜伏式武器为圆柱形物体, 从潜艇平台施放直至坐底之前大致可分为以下2个阶段。

1) 第1阶段即武器从潜艇上分离直至武器到达设定的分离深度。在此阶段武器在自身重浮力以及水动力的作用下, 初始时在下沉的同时还进行自转, 最终其姿态由水平转换至垂直状态。

2) 第2阶段即当武器达到设定的分离深度后, 采用分离减速方案来实现坐底。该方案实施过程如下: 当武器到达分离深度时, 开始分离为武器舱和压载舱两部分(见图1), 彼此间通过钢缆连接, 压载舱通过钢缆拖动武器舱下沉, 当压载舱到达海底时, 武器舱在其自身正浮力作用下逐渐减速, 最终被压载舱如锚雷一样悬挂在海底。

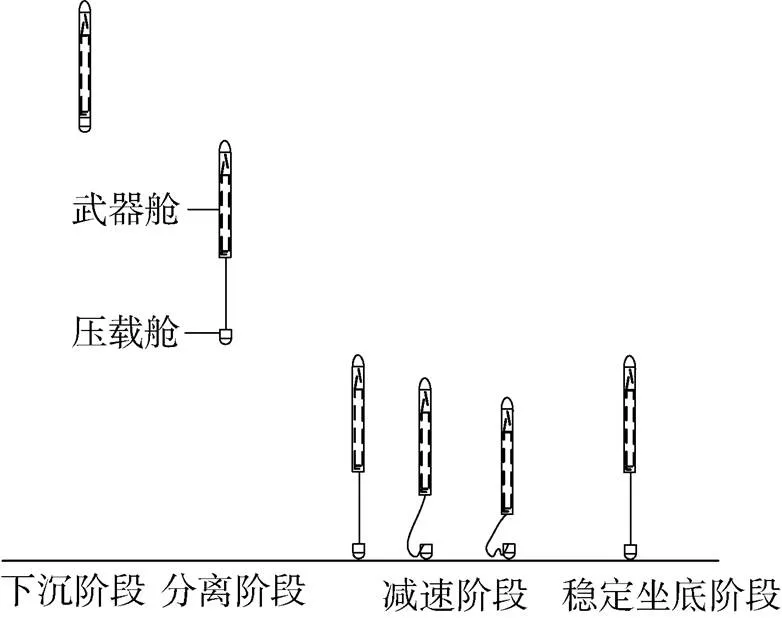
图1 潜伏式武器分离过程示意图

2 潜伏式武器水下施放后纵平面运动数学模型

2.1 建模坐标系

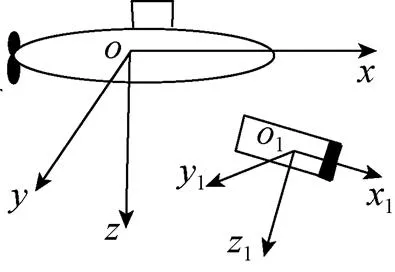
图2 固定坐标系和运动坐标系

为了简化建模过程, 建模中假定潜艇在静止条件下施放, 且不考虑初始施放阶段大攻角条件对武器水动力系数的影响, 以及在整个武器运动过程中水下海流的影响。

2.2 第1阶段数学模型

第1阶段为武器下沉直至分离前。经推导, 第1阶段的纵平面运动方程如下。

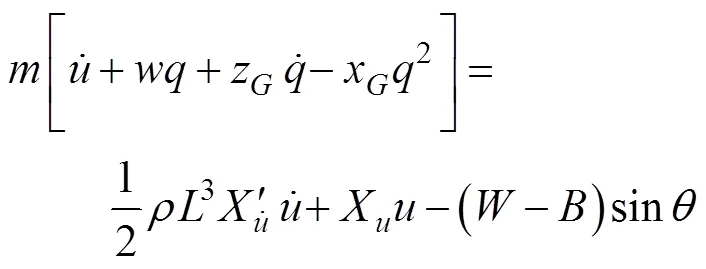
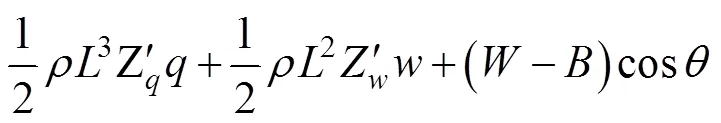
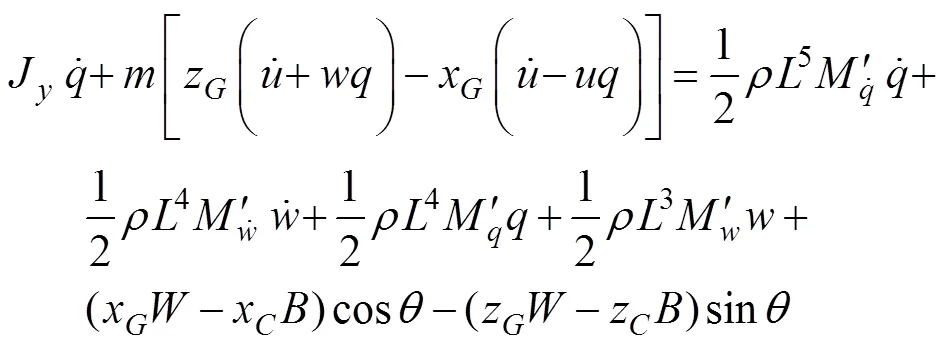
解以上方程可得在运动坐标系下的潜伏式武器任一时刻质心的加速度和绕质心的角加速度。

武器在固定坐标系下任一时刻的位置为

式中,v,v分别为武器在固定坐标系下,轴方向速度, 可按下式计算

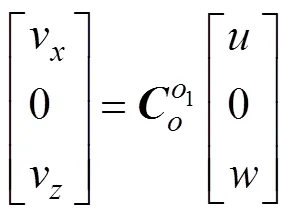
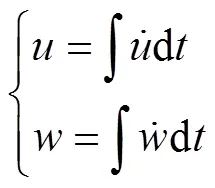
武器在任一时刻的姿态角为

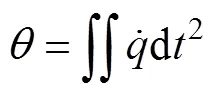
2.3 第2阶段数学模型

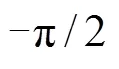
武器舱

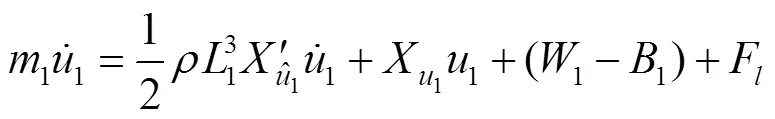
压载舱

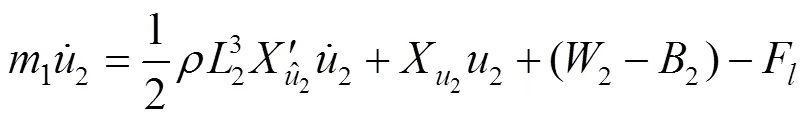
根据式(8)和式(9), 可解得任一时刻的加速度, 则运动坐标系下的任一时刻两舱段的速度为

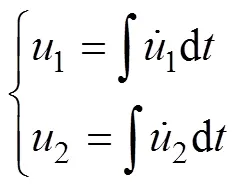
同理可通过坐标转换求得武器舱和压载舱在固定坐标系下的速度与位置。

因此在第2阶段运动建模的关键是求取分离后武器舱和压载舱之间的钢缆作用力。根据分离情况不同可分别按以下方法求取。

1) 钢缆拉直前

在武器刚分离直至钢缆拉直时, 作用在武器舱和压载舱之间钢缆作用力计算如下。

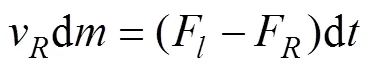
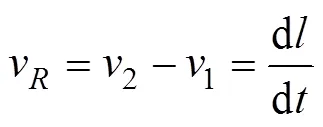
式(11)可改写成

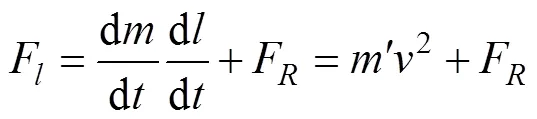
式中, , 为钢缆单位长度质量。

2) 钢缆拉直后

当武器的2个舱体分离距离大于钢缆最大长度时, 钢缆将拉直。此时作用在武器舱和压载舱的钢缆作用力可根据动能守恒和动量守恒定律进行计算。

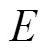
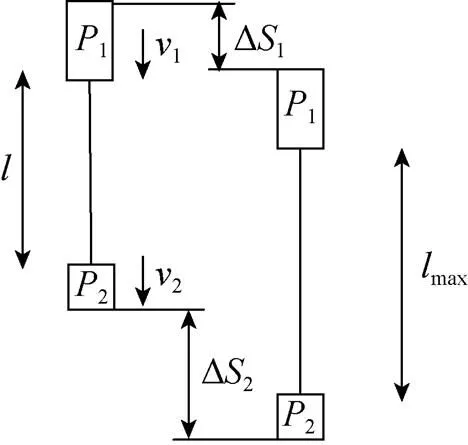
图4 钢缆拉伸过程示意图

器、海水阻力、钢缆张力所做的功, 即

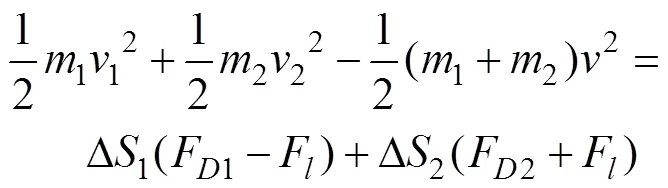
为了简化式(11), 参数取平均值

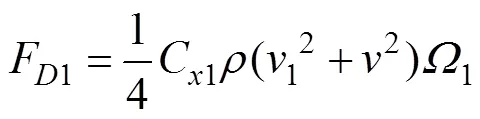
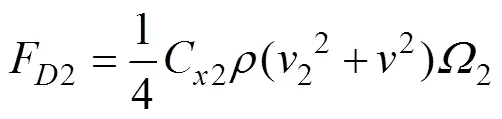
将式(18)、式(19)代入式(20), 得

则式(14)简化为

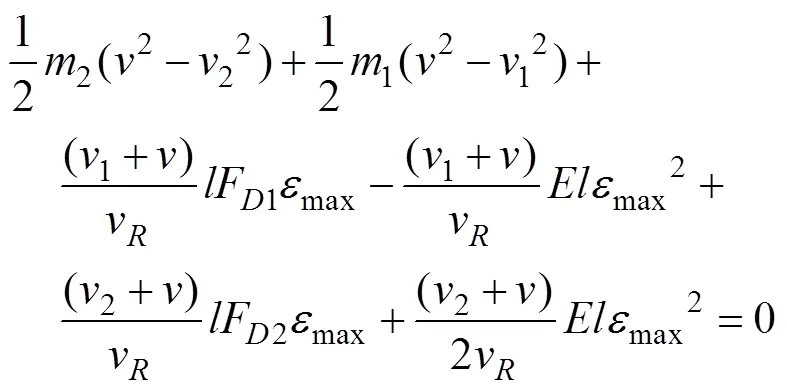
当忽略海水阻力的能量损失, 则武器整体拉直前后的动量守恒式为

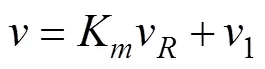
将式(25)代入(22), 得

令

则

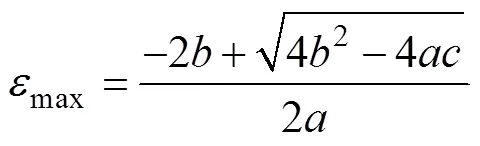
3 计算结果与分析

3.1 第1阶段运动仿真与分析

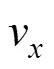
从以上仿真结果可以看出:

武器在施放后, 由于其重心与形心(动坐标原点)不重合, 因此除了自身转动外(见图7和图8), 其重心还围绕施放点垂线作类似钟摆运动(见图5), 并经过一段时间的摆动后, 最终武器保持竖直下沉方向;

图5 武器纵平面潜深曲线

图6 武器纵平面x向速度曲线

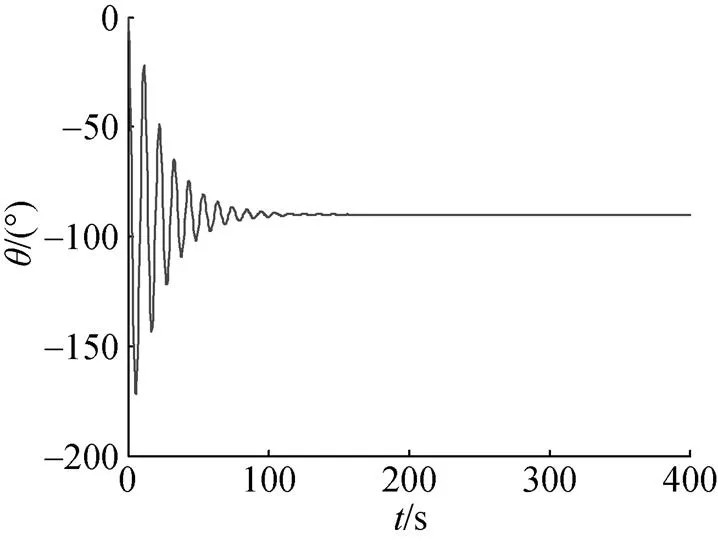
图8 武器纵平面纵倾角曲线

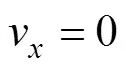
3.2 第2阶段运动仿真与分析

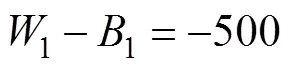
图9 武器舱与压载舱纵平面潜深变化曲线

从仿真结果可以看出:

1) 在水下2 700 m位置, 武器开始分离(见图9), 在分离过程中, 武器舱因正浮力的原因逐渐减速, 而压载舱则因负浮力突然增大而逐渐加速下沉, 两者之间的钢缆不断变长, 武器舱和压载舱的相对距离不断增加(见图9和图12)。

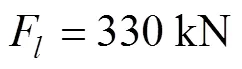
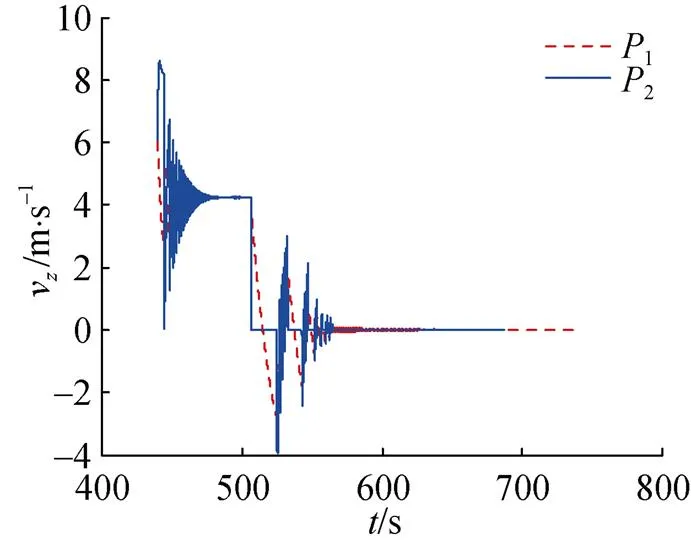
图10 武器舱与压载舱纵平面速度变化曲线

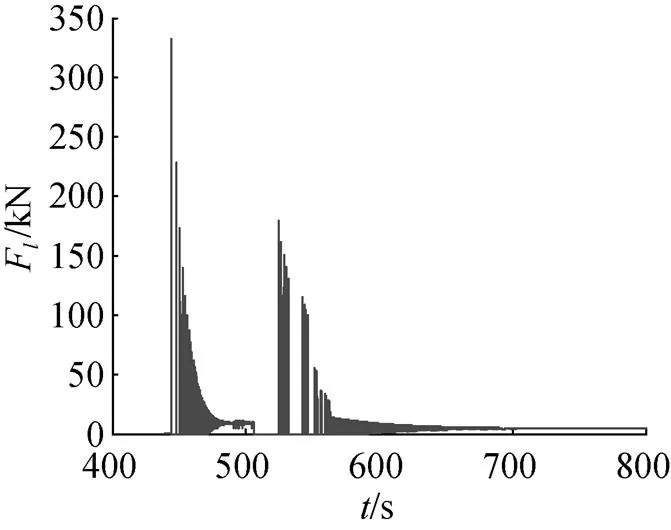
图11 钢缆拉力变化曲线

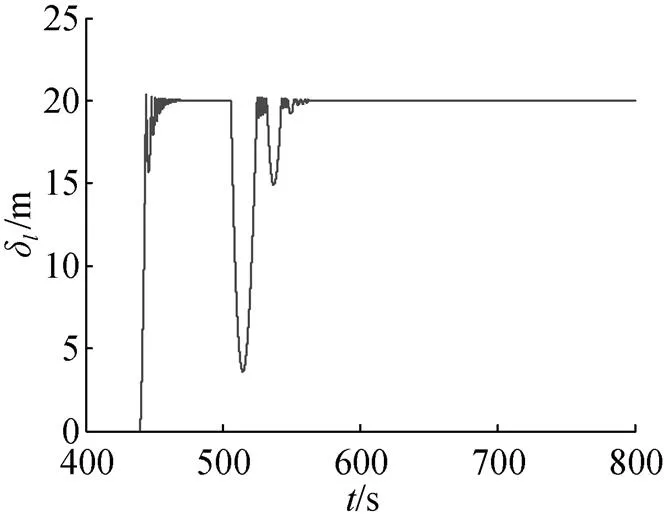
图12 武器舱与压载舱相对距离变化曲线

3) 当压载舱达到海底时, 武器舱因惯性继续下沉运动, 且下沉速度逐渐减小(见图10), 武器舱继续运动的最大惯性距离为16.4 m(见图12)。从两者的潜深曲线(见图9)可以看出, 经过减速下沉一段时间后, 当武器舱由于自身正浮力改为向上运动, 且其向上运动距离大于钢缆长度时, 钢缆将被拉直, 由于武器舱的向上运动惯性较大, 钢缆将会提起压载舱一起向上运动, 此刻钢缆受力, 武器舱和压载舱又将重复上述的运动, 直至武器舱的向上冲量瞬间无法提起压载舱, 则武器舱和压载舱将稳定停留在海底。

4 结束语

文中在分析了潜伏式武器水下施放运动过程的基础上, 针对武器施放后的不同运动阶段分别推导了相关数学模型, 并进行了仿真。结果表明:

1) 武器施放后初始阶段, 由于武器的重心和浮心不在其形心处, 因此在投放后的武器初期运动为其形心的下沉运动与绕形心钟摆式转动, 这种摆动随着下沉深度加大, 幅度逐渐减小直至成垂直下沉状态。

2) 分离减速方案可保证潜伏式武器的武器舱安全下沉到海底而不会发生冲击海底的情况, 而根据武器舱和压载舱的负浮力情况选择合适钢缆长度是确保武器舱安全着陆的关键, 如选择不合适, 则可能发生武器舱因惯性运动距离过大而撞击海底情况发生。因钢缆弹性及武器舱上浮惯性等原因, 分离减速方案不能保证压载舱一次着陆后就能稳定系留住武器舱, 往往会出现压载舱到达海底后又被武器舱提起的二次或多次着陆现象。

文中仿真未考虑大攻角条件下武器流体阻力系数变化以及水下涌浪的影响, 而且仿真中涉及的潜伏式武器的各种流体参数均是在准稳态条件下流场仿真获取的, 后续应开展动态条件及更接近实际状态条件下的潜伏式武器水下运动过程流场仿真, 以对潜伏式武器施放后的水下运动规律进行更为准确和深入的研究。

[1] 宋保维, 朱信尧, 梁庆卫, 等. 潜伏式无人水下航行器概念设计[J]. 火力指挥与控制, 2010, 35(8): 107-110.Song Bao-wei, Zhu Xin-yao, Liang Qing-wei, et al. Conceptual Design of Latent Unmanned Underwater Vehicle[J]. Fire Control and Command Control, 2010, 35(8): 107-110.

[2] 董阳泽, 刘平香. 远程潜伏式水声对抗器材概念及技术[J]. 舰船电子工程, 2007, 27(6): 7-9.Dong Yang-ze, Liu Ping-xiang. Primary Study on Long- range Underwater Acoustic Countermeasure[J]. Ship Elec- tronic Engineering, 2007, 27(6): 7-9.

[3] 周涛, 张晨光. 潜伏式鱼雷攻击性能分析[J]. 鱼雷技术, 2014, 22(2): 7-13.Zhou Tao, Zhang Chen-guang. Analysis on Attack Perfor- mance of Sleeping Torpedo[J]. Torpedo Technology, 2014, 22(2): 7-13.

[4] 宋保维, 陈良军, 丁浩, 等. UUV扑翼驱动机构设计及其运动仿真[J]. 机械设计, 2011, 28(4): 36-39.Song Bao-wei, Chen Liang-jun, Ding Hao, et al. Design and Kinematics Simulation of UUV’s Flapping Wing[J]. Journal of Machine Design, 2011, 28(4): 36-39.

[5] 王金强, 王聪, 魏英杰, 等. 飞翼式混合驱动水下滑翔机水动力与运动特性研究[J]. 兵工学报, 2018, 39(8): 1556-1564. Wang Jin-qiang, Wang Cong, Wei Ying-jie, et al. Hydrodynamic Properties and Motion Analysis of Hybrid-driven Underwater Glider with Flying Wings[J]. Acta Armamentarii, 2018, 39(8): 1556-1564.

[6] 潘瑛, 徐德民. 自主式水下航行器空间运动矢量建模与仿真[J]. 系统仿真学报, 2003, 15(4): 538-540. Pan Ying, Xu De-min. Vector Modeling and Simulation of the Autonomous Underwater Vehicle in Spatial Motions[J]. Acta Simulata Systematica Sinica, 2003, 15(4): 538-540.

[7] 胡坤, 张洪刚, 徐亦凡. 潜艇水下空间机动仿真与分析[J]. 计算机仿真, 2006, 23(5): 10-13.Hu Kun, Zhang Hong-gang, Xu Yi-fan. Simulation Study and Analysis on Underwater Space Motion of Submarine[J]. Computer Simulation, 2006, 23(5): 10-13.

[8] 刘正元. 潜水器大攻角范围内运动的仿真[J]. 船舶力学, 2005, 9(2): 54-59.Liu Zheng-yuan. Simulation of Submersible Motion in Large Attack Angle[J]. Journal of Ship Mechanics, 2005, 9(2): 54-59.

[9] 潘彬彬, 崔维成, 叶聪, 等. 蛟龙号载人潜水器无动力潜浮运动分析系统开发[J]. 船舶力学, 2012, 16(2): 58-71.Pan Bin-bin, Cui Wei-cheng, Ye Cong, et al. Development of the Unpowered Diving and Floating Prediction System for Deep Manned Submersible “JIAOLONG”[J]. Journal of Ship Mechanics, 2012, 16(2): 58-71.

[10] Gertler M, Hagen G R. Standard Equations of Motion for Submarine Simulation[R]. Washington D C: Naval Ship Research and Development Center, 1967.

Simulation on Motion in Vertical Plane of a Latent Weapon Released Underwater

LIAN Yong-qing1,2, SONG Bao-wei1, LI Zong-ji2

(1. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China;2. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

To study the motion law in vertical plane of a latent weapon released from submarine and the feasibility of using the separation and deceleration scheme to realize safe landing of the weapon, the motion process after release is divided into two stages: the first stage is from the latent weapon sinking until before separation, and the second stage is from separation beginning until weapon landing. Mathematical models are deducedrespectively for these two different stages of motion. And the whole motion process of the weapon is simulated. The characteristics of the initial motion are analyzed, and the weapon landing law according to the separation and deceleration scheme is obtained. Simulation result shows that the separation and deceleration scheme is feasible for safe landing of latent weapon.

latent weapon; separation and deceleration; motion in vertical plane

TJ012.3; E925.2

A

2096-3920(2019)04-0413-07

10.11993/j.issn.2096-3920.2019.04.008

练永庆, 宋保维, 李宗吉. 潜伏式武器水下施放后纵平面运动仿真[J]. 水下无人系统学报, 2019, 27(4): 413-419.

2019-11-19;

2019-12-18.

练永庆(1973-), 男, 博士, 副研究员, 研究方向为水中兵器总体及发射技术.

(责任编辑:许 妍)