超高速水下航行器控制方法研究热点综述

刘 伟, 范 辉, 吕建国, 杨贺然,2

超高速水下航行器控制方法研究热点综述

刘 伟1, 范 辉1, 吕建国1, 杨贺然1,2

(1 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077, 2 西北工业大学 航海学院, 陕西 西安, 710072)

超高速水下航行器借助超空泡减阻技术可以达到常规全沾湿航行器难以企及的200 kn以上的高航速, 对这类航行器的研究近年来呈现出由机理阐释向应用研究发展的主导趋势。在此趋势下, 针对超高速航行器控制方法的研究日益成为该领域的热点。文中首先给出了超高速水下航行器的概念, 继而综述了国内外最新研究进展, 随后提出并分析了若干热点研究问题, 包括对被广泛引用的Dzielski模型的讨论, 以及非线性滑行力、系统不确定性等动力学特性的研究热点, 和线型控制、反馈线性化、变结构控制、模糊控制等热点控制方法的优劣对比等, 最后对研究现状进行了总结, 展望了未来的发展方向, 提出对被控对象描述范围的拓展将是超高速水下航行器控制领域未来发展的主要驱动力, 同时智能控制也将成为超高速水下航行器控制方法的重要研究方向之一。

超高速水下航行器; 控制方法; 研究热点; 数学模型

0 引言

超高速水下航行器采用超空泡减阻技术, 使航行器所受阻力几乎降低了一个数量级, 因而航速可提升至常规水下航行器的3~4倍[1], 一举突破了水下航行的速度瓶颈, 具有重要的研究价值和广阔的应用前景。

超高速水下航行器涉及的技术领域十分广阔, 其总体设计和稳定控制是当前研究的重点和难点[2]。超空泡的包裹不仅使航行器阻力极大地减小, 同时也明显区别于传统全沾湿水下航行器的流体动力平衡模式。这方面相关研究早期集中于动力学建模和动态特性分析, 因此早期的相关综述主要集中于航行器概念的介绍[3]、模型的阐述、空化器和尾翼等流体动力的分析以及早期使用的控制方法简介[4]等。近年来, 随着学界对空泡机理研究的加深, 航行器后体非线性滑行力和系统不确定性的问题亟待解决, 而与之相关的航行器运动控制策略和方法也逐渐成为当前研究的热点。

文中主要综述了航行速度在50~200 m/s的超高速水下航行器的稳定控制方法。根据国内外最新研究进展, 综述了当前超高速水下航行器控制研究热点。从热点数学模型、热点对象特性和热点控制方法3个方面分析并总结了当前研究现状, 最后对超高速水下航行器控制方法的未来主要研究方向做出了合理预测。

1 超高速水下航行器概述

1.1 超高速水下航行器结构

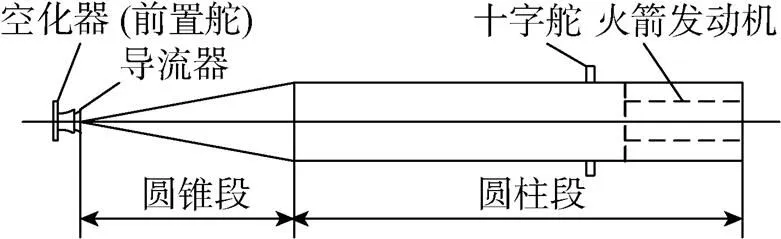
图1 超高速水下航行器外形图

超高速水下航行器的高航速是通过超空泡包裹航行器减小阻力得来的, 而超空泡在极大减小航行器所受流体阻力的同时也会让航行器丧失大部分浮力, 在这种前提下如何实现航行器的航行力学平衡, 这需要对其稳定运动模式进行合理设计[6]。

1.2 稳定运动模式

关于超高速水下航行器的稳定运动模式的研究, Savclenko[7]给出了4种超空泡航行器力学平衡运动模式, 如图2所示。

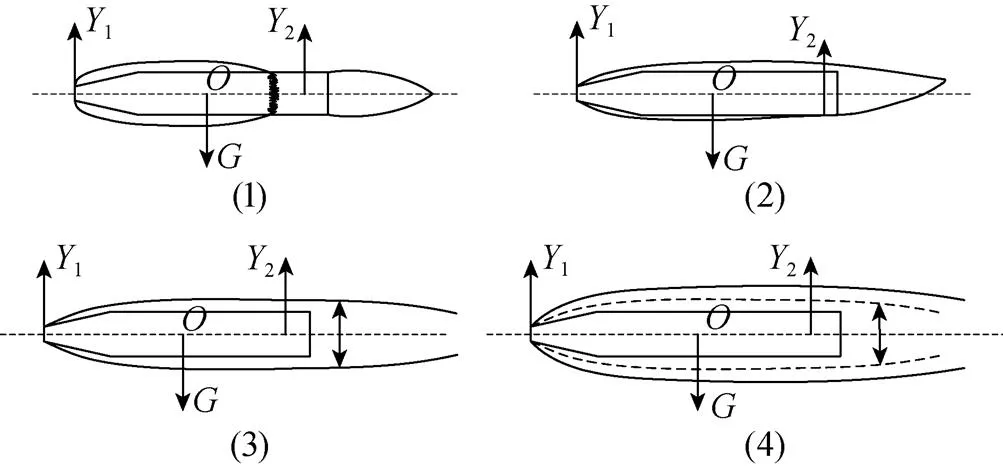
图2 超高速水下航行器4种稳定运动模式

目前针对超高速水下航行器控制方法的应用研究均基于上述模式2, 而模式1通常适用于超高速航行器过渡段的研究, 模式3和模式4则更多适用于超空泡射弹的研究。基于此, 文中综述的范围主要集中于基于模式2开展的超高速水下航行器控制方法的研究工作。

2 研究进展

2.1 国外研究进展

国外在超高速水下航行器控制方法研究方面的工作开展较早, 从近年来已公开发表的文献来看, 国外当前的研究热点在结合试验的控制性能研究和智能控制方法的应用方面。

为了能在实际流体条件中验证理论设计的控制方法性能, David设计了一个动态试验台[8], 在高速水洞中构建了一个可自由旋转的小比例超高速航行器模型(见图3), 可重现滑行力的振荡特性, 进而可对控制器的性能进行评估验证, 图4展示了诱导产生滑行力的试验情况。基于该试验平台, David完成了如下工作: 评估流体扰动对空化器和尾翼的影响[9], 指出了其对空化器的影响可忽略不计, 但对尾翼攻角的影响较大; 设计并验证了线性时不变(linear time invariant, LTI)输出反馈控制在非线性滑行力作用下的实际控制性能具有良好的鲁棒性[10], 同时还指出当航行器模型比例变大时, 空泡时延效应会更加明显, 必须要将时延特性考虑进实际控制器设计中。

图3 试验平台结构示意图

图4 后体滑行力诱导

Abolfazl等[11]宣称首次将智能控制方法引入超高速航行器的控制设计中, 设计了俯仰与深度控制系统, 控制器由2个独立的模糊比例微分(proportional derivative, PD)控制器和2个独立的前馈模糊神经控制器组成(见图5), 分别采用了mamdani和sugeno规则进行设计, 其中第1部分控制器用于控制深度, 第2部分控制器用于控制俯仰角。仿真结果表明, 所设计的智能控制器可以有效调节航行器深度和俯仰, 防止航行器跳水, 并且输入输出曲面变化率比较合理。

图5 智能控制系统框图

Seonhog等[12]针对超高速水下航行器在过渡阶段由于沾湿面积不断变化而导致的控制器控制效果恶化、控制系统稳定性变坏等问题, 提出了一种基于神经网络的自适应控制方法。经过相关数据训练过的适应神经网络可以使控制器在航行器模型不精确的情况下很好地进行俯仰控制, 同时双回路控制结构的设计也使得航行器能够很好地跟踪深度指令。

Yahyazadeh等[13]提出了一种参数优化迭代学习控制方法(parameter optimal iterative learning control, POILC), 以用于精确跟踪具有不确定参数的超高速水下航行器的俯仰角速度指令, 指出了航行器俯仰角速度控制具有非最小相位特性, 可以使用前馈控制来修正非最小相位引起的慢反应。采用POILC可以使用之前的控制数据不断迭代, 在连续的控制过程中不断提高控制器性能, 显著减低系统跟踪误差, 实现精确的前馈控制。

Mirzaei等[14]采用鲁棒模糊控制方法对航行器的非线性欠驱动行为(系统独立变量个数小于系统自由度个数)提出了广义间接自适应模糊滑模控制方法, 设计了实时自适应整定算法, 降低了滑模控制过程中的抖振现象, 减轻了系统稳态误差, 并且在存在传感器噪音和外部干扰情况下, 自适应模糊滑模控制器仍可以起到良好的作用。

从目前公开发表的文献来看, 近年来国外超高速水下航行器控制方法研究已不满足于理论仿真验证, 开始考虑应用实际流动条件来验证理论控制方法的性能, 可以更直观地发现控制算法在实际应用中可能存在的缺陷。此外, 国外越来越重视智能控制方法的运用, 从较简单的模糊PD控制到比较复杂的神经网络控制, 可见学界已经逐步发现经典控制理论在应对超高速水下航行器这种强非线性和非定常系统时的乏力, 智能控制的应用将是未来超高速航行器控制研究的一个重要发展方向。

2.2 国内研究进展

国内对超高速水下航行器控制方法的研究相比国外起步较晚, 但也取得了不小的进步。目前国内相关研究单位有中船重工第七〇五研究所、哈尔滨工业大学、哈尔滨工程大学和西北工业大学等。

许德智等[15]针对超高速水下航行器纵向运动特性, 提出了一种基于内外环的容错控制系统设计方法, 给出了执行器故障参数的估计算法和内环控制器的设计方法。仿真结果表明, 采用容错控制后的系统输出响应效果得到明显改善。

余晨菲等[16]针对巡航段的稳定控制问题, 提出了推力矢量/水舵复合的控制方案, 可以有效补偿由尾舵空化所引起的舵效不足, 同时将输入控制量多于输出被控量的多变量动态控制问题, 简化为单控制变量的动态控制问题, 从而使该方案在工程上易于实现。

陈超倩等[20-21]针对纵向运动非线性动力学模型存在的严重动态耦合与操纵耦合的问题, 通过输入输出的精确线性化和解耦设计最优控制器, 实现了对航行深度的渐近跟踪控制[20]; 针对航行器加速运动阶段的动力学及控制问题, 建立了更加精确的加速段非线性动力学模型, 并基于精确线性化方法设计了深度跟踪控制器, 实现了航行器在加速段变空化数条件下的深度跟踪[21]。

李洋等[22-24]以非全包裹超高速水下航行器为研究对象, 设计了一种反演滑模控制器以实现复合控制, 该控制器与单一变结构控制器相比, 超调量更小, 收敛速度更快[22]; 针对非全包裹航行器的姿轨控制问题, 对模型的未知干扰项设计了扩展状态观测器进行估计和补偿, 利用脉宽脉频调制方式解决了直接侧向力不可调下的控制输入调制问题[23]; 针对超高速航行器姿轨控制普遍存在的模型不确定性问题进行了相关研究, 针对模型中的未知函数利用径向基函数(radial basis function, RBF)神经网络进行了逼近并补偿[24]。

何朕和庞爱平[25-26]针对超高速水下航行器的沉浮和俯仰运动之间较强的动态耦合和航行器的动力学与运动学之间的耦合问题, 提出了内外回路设计的思想, 首先利用快速的内回路先将具有动态耦合的姿态回路进行镇定, 再以深度信号作为输出, 对主回路进行设计[25]; 针对尾拍现象, 采用扰动观测器补偿和消除影响, 并且控制面偏转角以满足正常工作范围的要求[26]。

近年来, 国内超高速水下航行器控制方法的研究呈现出多元化趋势, 针对航行器非线性滑行力、模型不确定性和运动耦合性等问题提出了包括线性二次型调节器(linear quadratic regulator, LQR)控制[27]、LPV控制[19]、滑模变结构控制[28]、基于反馈线性化的切换控制[29]和基于鲁棒理论的鲁棒变增益控制[30]等在内的许多理论可行的解决方案, 然而对这些方法的有效性和稳定性证明还停留在理论和仿真层面, 并且所基于的模型也是在诸多假设条件下推导而出的, 具有一定的理想性, 鲜有在真实流体条件下对控制性能进行的试验验证。

3 超高速水下航行器控制研究热点

3.1 热点数学模型

对于控制系统的研究, 首要问题是对被控对象的数学描述问题, 需要建立一个既能充分反映被控对象主要特性又不过于复杂的数学模型。

虽然已有研究采用6自由度模型[31], 但纵平面内2自由度模型仍然是被引用最多的模型。其中, 由Dzielski等[32]2003年提出的4状态2自由度模型引用的最为广泛, 诸如文献[15]~[28]等均是在此模型的基础上进行控制仿真研究。该模型基于如图6所示的超高速水下航行器的外形, 模型矩阵形式描述如下

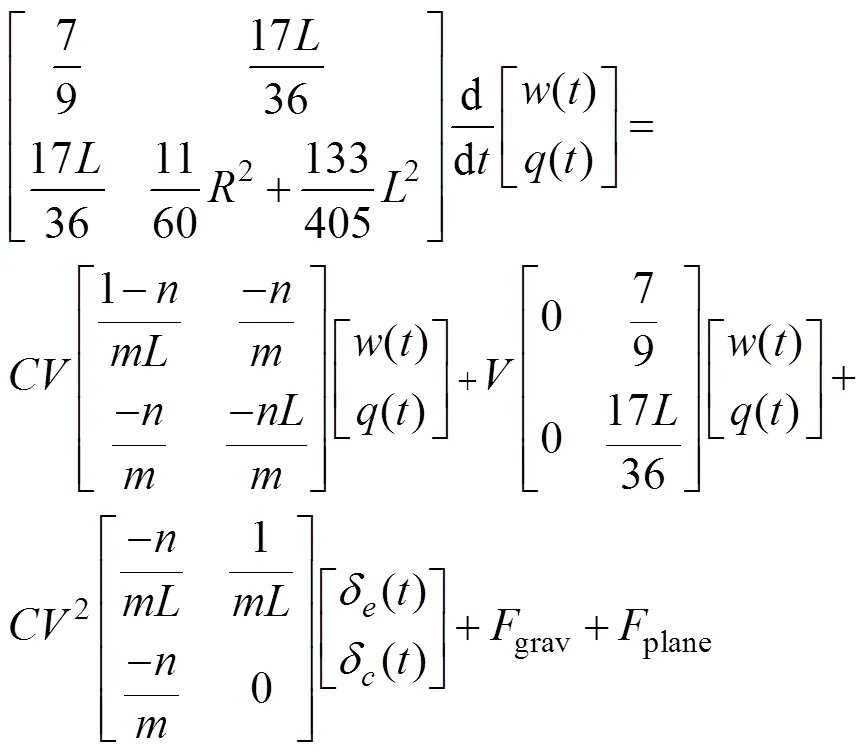
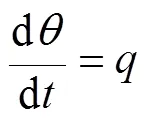
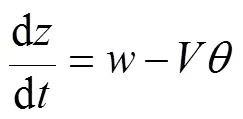
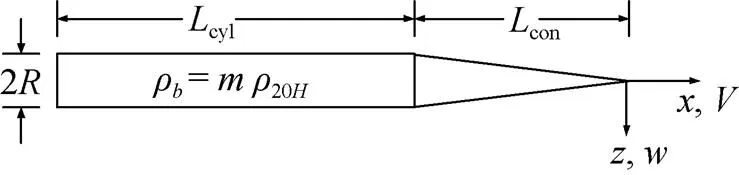
图6 Dzielski模型描述的超高速水下航行器外形图

采用简单的比例-积分-微分(proportional- integral-derivative, PID)控制方法可以实现系统的闭环稳定, 系统响应会迅速形成稳定的极限环, 航行器尾部周期性拍击下空泡壁, 且振幅稳定在一定幅度, 航行器渐近稳定。

Dzielski提出的模型很好地平衡了模型的准确性和复杂度之间的关系: 一方面, 该模型能良好地描述航行器纵平面运动特性, 突出体现非线性滑行力的振荡特性; 另一方面, 基于一定的合理简化条件, 将模型整合成状态空间形式, 便于开展线性化和控制律设计工作。因此大量水下超高速控制领域的文献直接引用此模型, 或在此模型基础上加上空化器偏转、尾舵效率不确定性、空泡记忆效应等因素进行一定的改进[33-36]。

3.2 被控对象特性研究热点

控制方法的研究本质上是对被控对象关键特性的应对方法研究。学界对于超高速水下航行器关键特性的研究热点目前集中于非线性滑行力和系统不确定性。

1) 非线性滑行力

对于滑行力方面, 主流措施是采取各种控制策略尽量抑制滑行力[9-10, 18-19], 并且希望滑行力能理论上收敛至零[20, 26]。

Dzielski模型中滑行力和航行器攻角关系如图7所示。

从图中看出, 滑行力存在一定的死区空间, 在一定的攻角阈值范围内滑行力始终为0, 此时航行器有着理想的工作状态, 即完全在空泡内运动, 后体不会和上下空泡壁发生接触。当航行器攻角超过该阈值时, 滑行力会随着攻角的增大而迅速增大, 后体会在狭小的空泡壁内上下摆动, 最终可能导致航行器运动失稳。

针对这种滑行力带来的振荡特性和非线性, David将航行器模型简化为一个带有时间延迟和死区非线性的LTI系统, 将滑行力抑制作为控制目标, 减小滑行力的同时增加了航行器可稳定跟踪的指令范围[37]。国内对此采用的办法有变结构切换控制和预测控制等。变结构切换控制针对滑行力存在死区的特点, 根据航行器有无滑行力采取不同的控制策略, 对无滑行力的情况可采用基于极点配置设计的控制器, 对有滑行力的情况则采用非线性控制器, 2个控制器联合形成非线性切换控制器, 文献[38]的仿真结果证明了该控制策略的有效性, 但也存在着所需控制力过大, 容易造成执行器饱和等缺点。预测控制是把与滑行力相关的量作为一个输出变量, 同时对该变量的取值范围进行约束, 将有约束控制转化为二次规划问题求解, 避免航行器后体与空泡壁面接触, 直接消除滑行力[39]。

2) 系统不确定性

对于系统不确定性, 主流措施是采用如滑模变结构控制和模糊控制等鲁棒性较好的控制方法, 尽量降低控制器对系统参数变化的敏感性[12,14,28,30,40]。

在模型中加入不确定项和干扰力, 系统变为

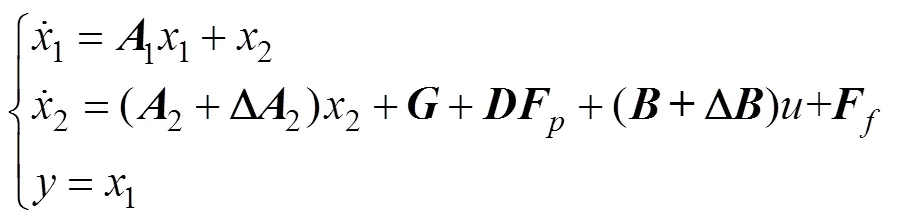
非线性滑行力和系统不确定性作为超高速水下航行器关键特性的原因有2点: 一是新, 空泡的包裹是超高速航行器区别于常规航行器的最重要特征, 也是其新颖性所在, 与其相伴产生的滑行力和系统不确定性也是常规水下航行器所不具有的, 需要重点分析; 二是难, 由于目前对空泡作用机理的研究仍不够充分, 滑行力和系统不确定性在现有技术条件下无法完全给出精确描述, 因此需要进行重点研究。

3.3 热点控制方法

当前超高速水下航行器的控制方法可分为线性控制方法和非线性控制方法2种类型。常用的线性控制方法包括状态反馈控制、LQR控制、最优控制等; 常用的非线性控制方法包括变结构控制、模糊滑模控制、反馈线性化方法等。相较于非线性控制方法, 线性控制方法更加简单且易于计算分析和实现, 因此在工程实践中得到了广泛应用, 但由于模型线性化过程中不可避免地存在精度损失, 因此在未来对控制精度要求越来越高的趋势下线性方法的局限性逐步突显出来; 而非线性控制方法更加全面地考虑航行器的非线性特性, 能够满足未来对于控制精度的要求, 但受限于当前的技术条件较难实现其控制器的工程设计, 因此限制了其实际工程应用。对目前的若干热点控制方法归纳如下。

1) 线性控制

线性控制方法需要在线性模型基础之上进行控制器的设计。超高速水下航行器的运动规律与常规水下航行器差别很大, 反而与导弹的运动规律相似, 因此可以借鉴导弹制导与控制系统中已被成熟运用的设计方法。例如, 导弹控制系统设计一般采用的小扰动线性化方法, 该方法基于小扰动原理将非线性运动方程组在设定的平衡点处线性化, 通过忽略次要的耦合条件, 将横滚、俯仰和偏航3个通道相互独立出来, 进而在线性模型基础上进行线性控制律的设计[40]。

线性控制方法技术上较容易实现, 可以实现基本的性能需求, 并且容易得到解析解, 从而大大提高计算机运算速度, 有利于提高系统的响应速度。然而超高速水下航行器是强非线性系统, 一旦出现航行器偏离平衡点较大的情况线性控制方法就会出现问题, 并且由于这种航行器特殊的航行方式, 其所受的干扰和噪声非常大, 而一般的线性控制方法很少考虑外界这些干扰对系统的影响, 系统鲁棒性较差, 因此一定程度上限制了线性控制方法在超高速水下航行器中的实际工程应用。

2) 反馈线性化

超高速水下航行器具有强非线性特征, 这种特征不仅体现在滑行力上, 也体现在不同自由度的动态耦合和操纵耦合上, 而小扰动线性化方法往往忽略了这种特征, 针对这一缺点, 提出了反馈线性化方法。

反馈线性化是一种精确线性化方法, 该方法通过状态变换和反馈来消除系统中的非线性, 在控制器设计过程中等效补偿系统中的非线性, 线性化过程中并未忽略任何高阶非线性项, 因此该方法不仅精确, 且具有整体性, 不会局限于平衡点附近, 而是对反馈线性化变换的整个区域都有效。反馈线性化方法使得线性控制方法的设计可以建立在不忽略航行器非线性的基础之上, 这是其最主要的优势, 但由于反馈线性化的系统实现比较复杂, 工程上目前较难实现其控制器的设计, 因此限制了其实际应用。

3) 变结构控制

不论是线性控制还是反馈线性化方法, 均要建立在被控系统精确模型的基础上, 然而由于空泡形成机理的复杂性以及实际航行中的参数摄动和外界扰动, 想要建立超高速水下航行器的精确模型是非常困难的, 因此对控制系统的鲁棒性提出了较高的要求。变结构控制往往包含滑动模态, 可以根据系统当前的状态, 有针对性地不断变化, 迫使系统按照预定的滑动模态运动, 而滑动模态可以根据系统性能指标进行设计, 并且只与系统状态有关, 因此对参数变化不灵敏, 抗干扰能力强, 被广泛地应用于超高速水下航行器的理论控制方法研究中。一种常见的变结构控制系统的设计就是根据系统所受滑行力的有无分别设计其控制器, 有滑行力时采用非线性控制, 无滑行力时采用线性控制, 二者联合形成变结构控制器, 往往有着较好的控制效果[38]。

由于变结构控制本质上是一种不连续控制, 在实际工程实践中, 状态检测误差、系统惯性, 以及切换系统开关特性的不理想性, 都会导致实际系统中存在抖振现象, 即系统不能准确按照滑动模态面的轨迹向平衡点运动, 而是在其平衡点来回波动[41]。抖振无法避免, 并且会导致系统很难实现精确控制, 系统高频未建模部分可能产生强烈的振动导致系统受损, 并且会增加控制系统的能量消耗, 因此抖振抑制问题的研究成为该方法能否突破其应用限制的关键。

4) 模糊控制

包括经典控制理论和现代控制理论在内的传统控制理论, 在面对具有参数结构时变、强非线性和强耦合性等特点的超高速水下航行器系统时, 往往很难设计和实现有效的控制, 而模糊控制的对象往往具有以下三方面特点[42]: 对象模型不确定, 模型知之甚少或者参数和结构在很大范围内变化; 具有非线性特性; 对象具有复杂的任务和要求, 因此模糊控制越来越多地被应用于超高速水下航行器的控制研究中。

模糊控制是一种智能控制, 甚至不需要控制对象的模型, 可以充分运用相关专家的经验, 并且理论上可以以任意精度逼近任何非线性函数, 模糊控制所具有的强鲁棒性和可独立于被控对象模型的特点使其非常适用于超高速水下航行器的控制。同时模糊控制还可以与滑模变结构控制进行组合, 从而有效地抑制其固有的抖振现象[1]。然而由于模糊控制发展较晚, 很多理论并不是十分成熟, 并且模糊控制具有分析定量系统能力欠佳, 模糊规则和量化只能通过反复试凑给出, 其稳定性理论证明困难等缺陷, 因此要将模糊控制广泛地应用于工程实践中仍有较长的路要走。

从上述内容可以看出, 由于当前条件下对于非线性滑行力和系统不确定性的研究仍不够充分, 缺乏已知的试验数据和实际的工程经验, 目前没有哪一类控制方法在试验中被证明是实际有效的, 整个超高速水下航行器控制系统的研究还处于理论方法的尝试阶段, 因此控制方法较为分散, 经典控制、现代控制、非线性控制和智能控制均被用于这种航行器的控制方法研究之中。部分热点控制方法的优缺点对比如表1所示。

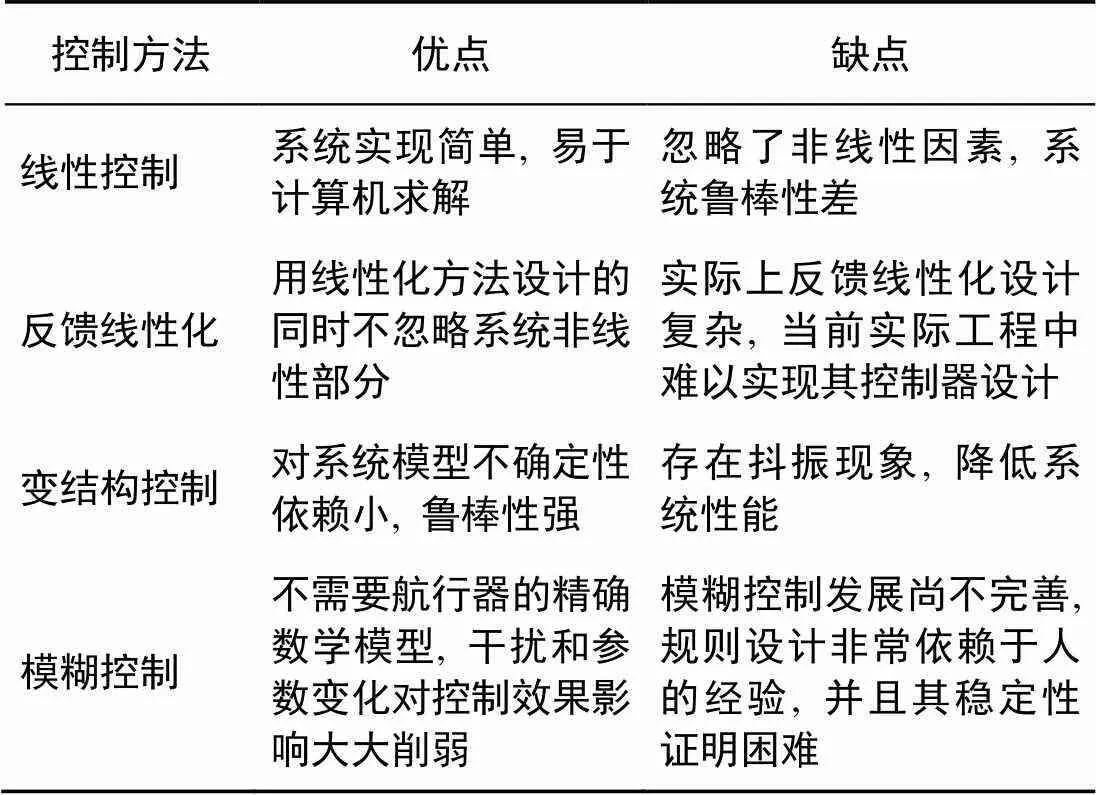
表1 热点控制方法优缺点对比

4 总结与展望

纵观当前超高速水下航行器控制领域的研究工作, 存在“两集中, 一分散”的特征。“两集中”一是指采用的数学模型比较集中, 普遍采用Dzielski模型开展研究, 二是针对的对象关键特性比较集中, 主要是对非线性滑行力的抑制与系统不确定性的应对; “一分散”是指学界采用的控制方法比较分散, 多数主流的控制方法都应用到这种航行器的控制研究中。

从以上总结的研究特征可以推论, 对被控对象描述范围的拓展将是超高速水下航行器控制领域未来发展的主要驱动力。这种拓展可能包括由集中研究超空泡充分包裹航行器的高速巡航段控制问题, 向研究部分空泡包裹的过渡段控制问题拓展; 也可能包括从集中研究定深直航稳定控制问题, 向研究高速回旋机动稳定控制问题拓展。

随着智能控制学科的崛起, 已有学者成功地将模糊控制和人工神经网络控制方法应用到超高速水下航行器纵向运动控制中, 并取得了良好的控制效果, 因此智能控制将是未来超高速水下航行器控制策略发展的一个重要研究方向。

[1] 刘富明. 超空泡航行器纵向运动控制[D]. 哈尔滨: 哈尔滨工程大学, 2015.

[2] 李凝, 杨飚. 德国轻型超空泡鱼雷研发现状及展望[J]. 鱼雷技术, 2008, 16(2): 1-4.Li Ning, Yang Biao. R&D Status Quo and Perspective of Light weight Supercavitating Torpedo in Germany[J]. Torpedo Technology, 2008, 16(2): 1-4.

[3] 王改娣. 超空泡鱼雷技术特点分析[J]. 鱼雷技术, 2007, 15(5): 1-4.Wang Gai-di. Analysis of Technical Features of Supercavitating Torpedoes[J]. Torpedo Technology, 2007, 15(5): 1-4.

[4] 赵新华, 孙尧, 安伟光, 等. 超空泡航行器控制问题研究进展[J]. 力学进展, 2009, 39(5): 537-545.Zhao Xin-hua, Sun Yao, An Wei-guang, et al. Advances in Supercavitating Vehicle Control Technology[J]. Advances in Mechanics, 2009, 39(5): 537-545.

[5] Rand R, Pratap R, Ramani D. Impact Dynamics of a Supercavitating Underwater Projectile[R]. ASME Design Engineering Technical Conferences. Sacramento, California: ASME, 1997

[6] 吴振. 基于水洞试验的通气超空泡航行器的控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.

[7] Savchenko Y N. Control of Supercavitation Flow and Stability of Supercavitation Motion of Bodies[R]. RTO-EN010 AVT Lecture Series on Supercavitating Flows. Brussels. Belgium, 2001: 313-329.

[8] Escobar D, Vollmer D, Arndt R. A Dynamic Test Bed for Supercavitating Vehicle Control[J]. Journal of Physics: Conference Series, 2015, 656(1): 012144.

[9] Escobar D, Balas G, Anrdt R. Modeling, Control, and Experimental Validation of a High-Speed Supercavitating Vehicle[J]. IEEE Journal of Oceanic Engineering, 2015, 40(2): 362-373.

[10] Escobar D, Anrdt R. Robust Control of a Small-Scale Supercavitating Vehicle: from Modeling to Testing[J]. Ocean Engineering, 2018, 160: 412-424.

[11] Mardani A, Danesh M, Karimi B. Fuzzy/Neuro-Fuzzy Depth and Pitch Regulating Control of a Supercavitating Vehicle[C]//The 19thIranian Conference on Electrical Engineering. Tehran, Iran: ICEE, 2011.

[12] Seonhong K, Nakwan K. Neural Network Based Adaptive Control for a Supercavitating Vehicle in Transition Phase[J]. Journal of Marine Science and Technology, 2015, 20(3): 454-466.

[13] Yahyazadeh M, Ranjbar A. High Performance Tracking of High-Speed Supercavitating Vehicles with Uncertain Parameters Using Novel Parameter-Optimal Iterative Lear- ning Control[J]. Robotica, 2015, 33(8): 1653-1670.

[14] Mirzaei M, Eghtesad M, Alishahi M M. A New Robust Fuzzy Method for Unmanned Flying Vehicle Control[J]. Journal of Central South University, 2015, 22(6): 2166- 2182.

[15] 许德智, 姜斌, 钱默抒. 基于内外环设计的超空泡航行器容错控制[J]. 济南大学学报, 2014, 28(1): 60-64.Xu De-zhi, Jiang Bin, Qian Mo-shu. Fault Tolerance Control of Supercavitating Vehicles Using Inner and Outer Loop Design[J]. Journal of University of Jinan, 2014, 28(1): 60-64.

[16] 余晨菲, 林鹏, 周军. 基于推力矢量/水舵复合的超空泡导弹变结构控制研究[J]. 西北工业大学学报, 2014, 32(5): 805-810.Yu Chen-fei, Lin Peng, Zhou Jun. Variable Structure Research on Supercavitating Vehicle Based on Thrust Vector/Rudder Combination[J]. Journal of Northwestern Po- lytechnical University, 2014, 32(5): 805-810.

[18] 韩云涛, 强宝琛, 孙尧, 等. 基于圆判据的超空泡航行器非线性控制研究[J]. 工程力学, 2015, 32(8): 236-242.Han Yun-tao, Qiang Bao-chen, Sun Yao, et al. Non-linear Control Research on Supercavitating Vehicles Based on Circle Criterion[J]. Engineering Mechanics, 2015, 32(8): 236-242.

[20] 陈超倩, 曹伟, 王聪, 等. 超空泡航行器最优控制建模与仿真[J]. 北京理工大学学报, 2016, 36(10): 1031-1036.Chen Chao-qian, Cao Wei, Wang Cong, et al. Modeling and Simulating of Supercavitating Vehicles Based on Optimal Control[J]. Transactions of Beijing Institute of Technology, 2016, 36(10): 1031-1036.

[21] 陈超倩, 曹伟, 王聪, 等. 超空泡航行器加速段控制设计[J]. 哈尔滨工业大学学报, 2016, 48(8): 147-151.Chen Chao-qian, Cao Wei, Wang Cong, et al. Acceleration Stage Control Design for Supercavitating Vehicle[J]. Journal of HarbinInstitute of Technology, 2016, 48(8): 147-151.

[22] 李洋, 刘明雍, 张小件, 等. 非全包裹超空泡航行器建模与反演变结构控制[J]. 西北工业大学学报, 2016, 34(2): 215-221.Li Yang, Liu Ming-yong, Zhang Xiao-jian, et al. Modeling and Back Stepping Variable Structure Control for a Incomplete Encapsulated Supercavitating Vehicle[J]. Journal of Northwestern Polytechnical University, 2016, 34(2): 215-221.

[23] 李洋, 刘明雍, 杨盼盼, 等. 非全包裹超空泡航行器建模与姿轨控制[J]. 控制理论与应用, 2017, 34(7): 885- 894.Li Yang, Liu Ming-yong, Yang Pan-pan, et al. Modeling and Attitude-Orbit Control for Incomplete-Encapsulated Supercavitating Vehicles[J]. Control Theory & Applications, 2017, 34(7): 885-894.

[24] 李洋, 刘明雍, 张小件. 基于自适应RBF神经网络的超空泡航行体反演控制[J/OL]. 自动化学报, 2018, 44(X): 1-10. [2018-04-18]. http://kns.cnki.net/kcms/detail/11.21 09.TP.20180418.1444.004.html. Li Yang, Liu Ming-yong, Zhang Xiao-jian. Adaptive RBF Network Based on Backstepping Control for Supercavitating Vehicles[J/OL]. Acta Automatica Sinica, 2018, 44(X): 1-10. [2018-04-18]. http://kns.cnki.net/kcms/detail /11.21 09.TP.20180418.1444.004.html.

[25] 何朕, 庞爱平. 超空泡航行器的反馈控制设计[J]. 电机与控制学报, 2017, 21(8): 101-108.He Zhen, Pang Ai-ping. Feedback Control Design for Supercavitating Vehicles[J]. Electric Machines and Control, 2017, 21(8): 101-108.

[26] 庞爱平, 何朕. 超空泡航行器的扰动观测器补偿设计[J]. 电机与控制学报, 2018, 22(1): 107-113.Pang Ai-ping, He Zhen. Disturbance Observer and Compensation Design for Supercavitating Vehicles[J]. Electric Machines and Control, 2018, 22(1): 107-113.

[27] 高浩楠. 水下高速航行器制导与控制一体化研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.

[28] 王志学. 水下高速航行器纵向控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

[29] 赵丹. 超空泡航行器双通道控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

[30] 韩云涛, 程章龙, 李盼盼, 等. 超空泡航行器LPV鲁棒变增益控制[J]. 华中科技大学学报(自然科学版), 2017, 45(7): 127-132.Han Yun-tao, Cheng Zhang-long, Li Pan-pan, et al. Robust Variable Gain Control for Supercavitating Vehicle Based on LPV[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2017, 45(7): 127-132.

[31] 范辉. 超空泡航行器动力学建模与仿真研究[D]. 西安: 西北工业大学, 2009.

[32] Dzielski J, Kurdila A. A Benchmark Control Problem for Supercavitating Vehicles and Aninitial Investigation of Solutions[J]. Journal of Vibration and Control, 2003, 9(7): 791-804.

[33] Nguyen V, Balachandran B. Supercavitating Vehicles With Noncylindrical, Nonsymmetriccavities: Dynamics and Instabilities[J]. Journal of Computational & Nonlinear Dynamics, 2011, 8(2): 219-242.

[34] Lv R, Yu K, Wei Y. Adaptive Robust Controller for Supercavitating High-Speed Bodies[J]. Journal of Harbin Institute of Technology, 2011, 18(4): 77-81.

[35] Qiang B, Han Y, Sun Y. Absolute Stability Control of Supercavitating Vehicles Based on Backstepping[C//Pro- ceeding of 2014 IEEE International Conference on Mechatronics and Automation. Tianjin, China: IEEE, 2014: 1918-1923.

[36] Hassouneh M A, Nguyen V, Balachandran B, et al. Stability Analysis and Control of Supercavitating Vehicles with Advection Delay[J]. Journal of Computational and Non- linear Dynamics, 2013, 8(2): 021003-1-021003-10.

[37] Sanabria D S, Balas G. Planing Avoidance Control for Supercavitating Vehicles[C]//2014 American Control Conference(ACC). Portland, Oregon, USA: ACC, 2014.

[38] 魏英杰, 王京华, 曹伟. 水下超空泡航行器非线性动力学与控制[J]. 振动与冲击, 2009, 28(6): 179-182.Wei Ying-jie, Wang Jing-hua, Cao Wei. Nonlinear Dynamics and Control of Underwater Supercavitating Vehicle[J]. Journal of Vibration and Shock, 2009, 28(6): 179-182.

[39] 王京华, 张嘉钟, 魏英杰, 等. 超空泡高速航行器动力学建模与控制设计[J]. 哈尔滨工业大学学报, 2010, 42(9): 1351-1355.Wang Jing-hua, Zhang Jia-zhong, Wei Ying-jie, et al. Dynamics Modeling and Control Design for a High-speed Supercavitating Vehicle[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1351-1355.

[40] 王雨. 水下高速航行器航向控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[41] 田宏奇. 滑模控制理论及其应用[M]. 武汉: 武汉出版社, 1995.

[42] 曾光奇, 胡均安. 模糊控制理论与工程应用[M]. 武昌: 华中科技大学出版社, 2006.

Review of Research Hotspots of Superspeed Undersea Vehicle Control Methods

LIU Wei1, FAN Hui1, LÜ Jian-guo1, YANG He-ran1,2

(1 The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 2 School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

With the help of supercavitation drag-reduction technology, the speed of the superspeed undersea vehicle could reach over 200 kn, and this is difficult for conventional fully wet vehicles. In recent years, the researches on this kind of vehicles have shown a leading trend from mechanism to application. Under this trend, control method of superspeed undersea vehicle has become a hotspot in this field. In this paper, the concept of the superspeed undersea vehicle is given, and the latest progress at home and abroad is reviewed. Then several hot research issues are put forward and analyzed, including the discussion about the widely quoted Dzielski model, and the dynamic characteristics such as nonlinear sliding force and system uncertainty, as well as the comparison among the popular control methods, such as linear control, feedback linearization, variable structure control, and fuzzy control. Finally, the latest researches are summarized, and future development directions are prospected. It is pointed out that expansion of the description range of controlled object will be the main driving force on future development of superspeed undersea vehicle control, and intelligent control will also become one of its important research directions.

superspeed undersea vehicle; control method; research hotspot; mathematic model

TJ630.33; U674.941

R

2096-3920(2019)04-0369-10

10.11993/j.issn.2096-3920.2019.04.002

刘伟, 范辉, 吕建国, 等. 超高速水下航行器控制方法研究热点综述[J]. 水下无人系统学报, 2019, 27(4): 369-378

2019-03-01;

2019-04-02.

刘 伟(1994-), 男, 在读硕士, 主要研究方向为水下航行器控制与导航.

(责任编辑: 陈 曦)