人行荷载下大跨度楼盖MTMD参数与位置联合优化方法研究

唐斯聪， 王海龙,， 张晓冉， 胡子阳， 曹文静

(1. 石家庄铁道大学 交通运输学院，石家庄 050000; 2. 河北建筑工程学院 土木工程学院，河北 张家口 075000)

调谐质量阻尼器(Tuned Mass Damper,TMD)作为一种减振装置，通过调谐自身频率实现对主体结构的吸振减振。为了高效发挥TMD在工程实际中的作用，众多学者将新构造[1-2]、新理论[3-4]、新策略[5]紧密地与TMD系统结合，设计出了功能更强大、使用更方便的振动控制系统。多重调谐质量阻尼器(Multiple TMD,MTMD)是由多个单调谐质量阻尼器(Single TMD,STMD)构成的减振系统，在振动控制中较STMD拥有更佳的减振性能和控制鲁棒性，其因良好的经济性、优异的减振性能和易于安装维护的特点在工程结构减振中得到了广泛应用。由于MTMD较STMD复杂，在减振控制中要求多个TMD协同工作，MTMD的参数取值和位置选取成为决定减振效果的关键因素。

在参数取值方面，MTMD不像STMD一样能够利用解析方法寻找参数最优解，早期对MTMD的研究都是在特定参数下进行的[6]，通过指定TMD的频率、阻尼比和质量比，研究体系在应对地震荷载、风荷载等情况下的减振性能，初步得出了一些较为合理的MTMD参数组合[7-8]。随着最优算法与MTMD参数寻值结合，MTMD的参数不再停留在特定组合上，通过合理的优化能够得到特定情况下的最优解，徐庆阳等[9]根据大跨悬挂结构的动力特性将TMD分组设计，针对不同的模态优化不同组TMD参数，李泉等[10]针对大跨度楼盖结构的多模态振动问题，提出了MTMD对楼盖多个振动模态进行控制的设计方法，并比较了多模态优化方法和单模态优化方法设计的MTMD减振控制效率，徐若天等[11]提出一种步行荷载下大跨楼盖MTMD参数优化的混合算法，利用有限元获得楼盖模态后再由振型分解法计算步行荷载引起的结构响应，结合遗传算法对MTMD进行参数优化。

在位置选取方面，TMD不同安放位置对体系减振效果的影响及其在减振控制中的实现途径尚不明确，MTMD的位置设计尚无较为完善的方法，在安装MTMD的时候都按照STMD单模态控制的经验，将TMD布置于受控模态振型幅值的最大处，这种方法没有经过严密的推导，为此有一些学者通过自行编写的优化程序调用有限元软件，通过生死单元来模拟不同的位置组合，当结构复杂或TMD数量较多时，其计算量将是十分巨大的。

为了对MTMD的位置进行优化，克服有限元时程方法计算成本过高的问题，本文结合有限元法和振型分解法，提出了一种MTMD位置优化方法，并以此为基础制定了MTMD位置和参数联合优化策略。

1 楼盖MTMD系统耦合运动方程

大跨度楼盖结构在使用过程中由于人行荷载的竖向激励可能产生较大的振动，会引起人体不适并影响建筑使用要求，需要对楼盖采取竖向振动控制措施，现利用MTMD对楼盖结构进行振动控制。被简化为n个质点的大跨度楼盖结构在人行激励下发生振动，在结构上布置m个TMD系统以控制振动响应，人行荷载设定为全体人员均匀分布在激励位置做同频率、同相位原地运动。整个体系的动力方程为

(1)

式中：M,C,K和Md,Cd,Kd分别为结构和MTMD的质量矩阵、阻尼矩阵、刚度矩阵；X为大跨结构各质点相对于地面的位移；Xd为各个TMD相对于地面的位移；E为n行m列的MTMD位置矩阵，E的每一列都对应一个TMD的安放位置，如：E矩阵第a列的元素为[0,0,…,1,…,0](1在矩阵第k行)，表示第a个TMD安放在结构第k个节点处。

MTMD相对大跨度楼盖的质量比很小(通常在5%以下)，可以认为对楼盖振型的影响很小。利用振型分解法将式(1)展开，并做方程间的代换，可推得：

(2)

(3)

式中：mn，cn，kn分别为第n阶的模态质量、模态阻尼和模态刚度；mm，cm，km分别为第m个TMD的质量、阻尼和刚度；qn为第n阶模态的广义坐标；xm为第m个TMD相对于地面的位移；φnm为第n阶模态在第m个质点处的振型幅值。

从式(2)右端可知，任何一阶模态响应都由全部TMD控制，它们或多或少的以惯性力的方式作用在各阶模态上，通过与振型幅值相乘表现出不同的参与程度。从单个模态来看，影响每个惯性力大小的因素是不同位置的振型幅值，从单个TMD来看，决定其在不同模态参与程度的因素是不同模态的振型幅值。

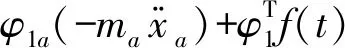
对式(2)、式(3)整体进行傅里叶变换，可得

X=E-1F

(4)

其中，

式中：F(iω)为步行荷载在频域的表现形式；ψn为与人员分布相关的n阶振型相关的系数，为人员活动区域覆盖的振型网点的竖向振型幅值之和；γ为与人员密度相关的系数。

依据大量单步落足曲线试验结果，脚步力荷载可用式(5)[13]的傅里叶级数表达，将其转换到频域可以表达为图1。

(5)

式中：G为行人平均重力；f0为行人步频；αi和σi分别为第i阶简谐振动荷载系数和初相位，α1=0.4+0.25(f0-2)，α2=α3=0.1；n为傅里叶级数阶数，一般取n=3。

图1 人行荷载在频域内的分布Fig.1 Distribution of human-induced loads in frequency domain

在计算ψn值时，首先对大跨度楼盖结构进行模态分析，选取需要叠加的模态数量，并提取各阶模态在楼盖网点处的竖向振型幅值，然后根据不同工况荷载的激励区域计算区域处的网点振型幅值之和，可得到n阶模态的ψn值。如：通过某楼盖模态分析的结果得知此楼盖结构在计算动力响应时需要考虑前五阶模态振动，工况A的人员活动位置位于楼盖的跨中区域，将跨中区域等间布置m个网点，提取前五阶模态在m个网点处的竖向振型幅值分别相加，得出工况A的ψ1～ψ5。

在得出上述参数后，利用结构动力学的相关知识得出本文计算结构响应的核心公式

(6)

2 大跨度楼盖结构MTMD优化方法与优化设计

2.1 结构布置及有限元分析

某体育馆二层楼盖结构为张弦梁-混凝土板组合楼盖结构。张弦梁跨度40 m，自西向东排列共13榀，每榀之间有次梁连接，张弦梁两端支承在混凝土柱的变截面位置，通过在钢梁支座区域设置长圆孔实现滑动端的自由滑动，在楼板拆模后焊死，钢梁截面规格为H900×450×25×50，撑杆采用空心圆钢管截面，杆件规格为Ø159×6，拉索采用高矾索，规格为1×397，钢梁与楼板之间利用混凝土楼板厚150 mm。尽管结构强度满足规范要求，但结构振动的峰值加速度超过人体舒适度耐受极限，容易引起人们的不适，造成恐慌心理，需对其进行减振设计。

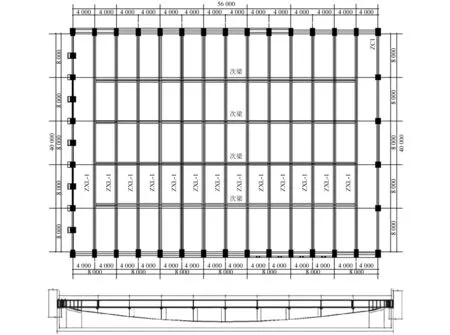
图2 楼盖平面图、弦支梁构造图Fig.2 Plan of floor structure and detail of beam string structure

模拟施工过程，利用实体单元模拟楼板和钢梁，采用绑定约束模拟栓钉实现两者的协同变形，利用杆单元模拟撑杆和拉索，对整体楼盖结构建立三维有限元模型。

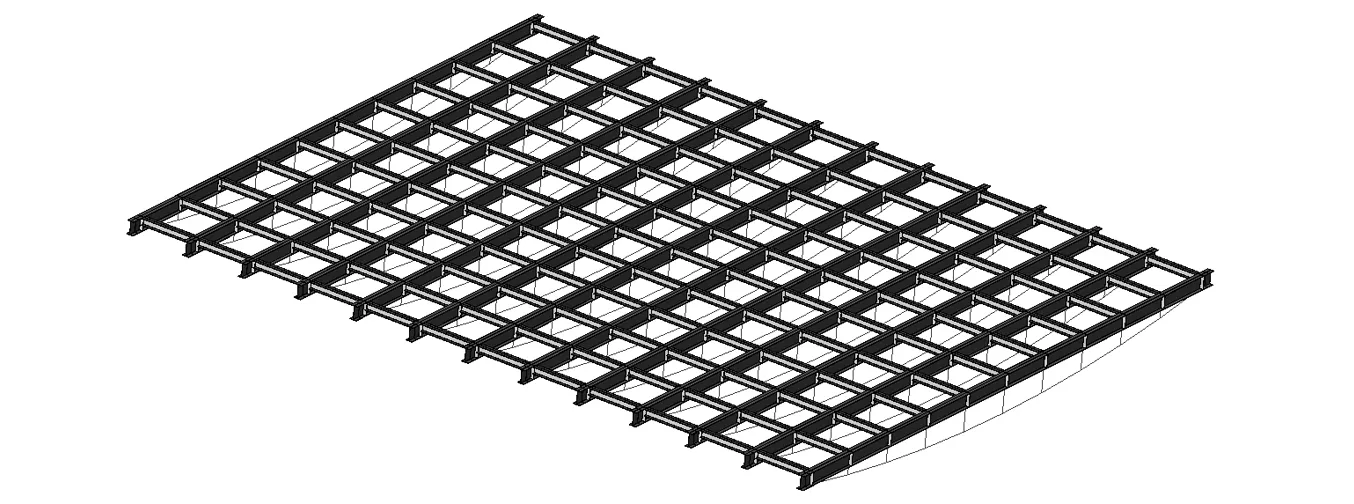
图3 弦支梁骨架模型Fig.3 The finite element model of beam string structure

图4 弦支梁-混凝土组合楼板模型Fig.4 The finite element model of cable supported beam structure-concrete slab composite floor

对楼盖结构进行模态分析得到各阶模态频率、质量参与系数，因大跨度楼盖结构在人行荷载激励下会发生以竖向为主的振动，整理楼盖结构的竖向振型，分析发现结构的一阶、三阶模态的振型质量参与系数之和达到97.9%，占竖向振型的绝大部分，故选取一阶、三阶模态为受控模态参与MTMD优化。图5为此楼盖结构一阶、三阶模态。

图5 组合楼盖模态形状和模态频率Fig.5 Natural frequencies and mode shapes of floor

2.2 MTMD位置优化方法

为了对MTMD的安放位置进行优化，需要对楼盖平面布置网点，由式(2)可知TMD提供的控制力与振型幅值成正比，故稀疏或忽略各阶模态振型幅值近零的网点，依据荷载和结构的对称性，忽略一些局部布置的差异，最终在楼盖约1/8部分选取512个点，如图6、图7所示。对其从1～512进行编号，在确定最优位置之前，这些点都为TMD可能的布置点，由此带来的位置组合多达上亿种，随着TMD数量的增加，组合的数量还会呈指数增长，经过比较选用遗传算法对MTMD进行优化。

遗传算法是一种借鉴生物界自然选择和自然遗传机制开发的随机搜索算法，它通过对决策变量进行编码，在编码的基础上对其进行选择、交叉、变异，在搜索过程中自动获取和累积相关搜索知识，并自适应地控制搜索过程以求得最优解。此算例中决策变量为网点的编号，映射到公式中与其对应的是网点所处位置的振型幅值，模型的一阶、三阶模态为受控模态参与MTMD优化，提取一阶、三阶模态在512个楼盖网点处的竖向振型幅值，组成振型矩阵，在优化过程中通过网点编号调用不同模态的振型幅值，虽然在优化过程中控制的变量是网点编号，但实际参与决策的是振型幅值，图8为种群中的单个个体参与优化的决策途径。

图6 网点布置位置Fig.6 Location of lattice point

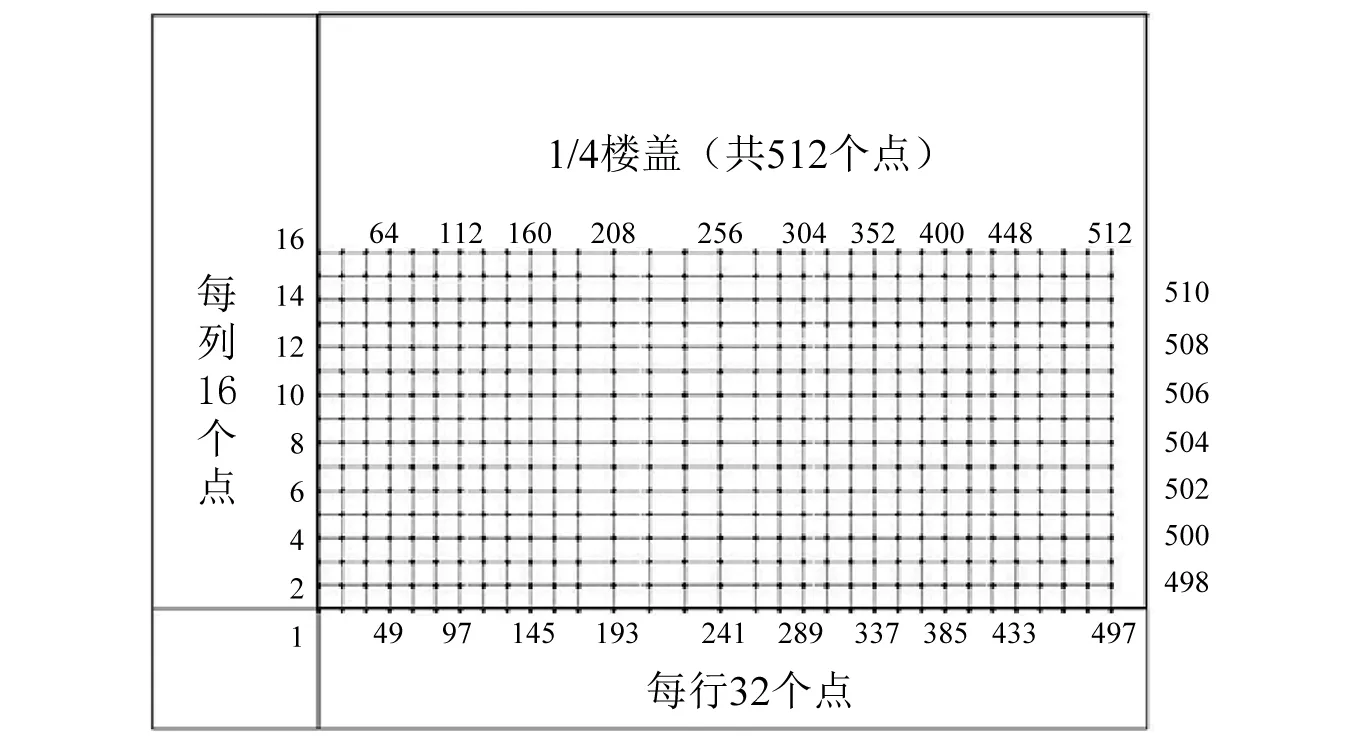
图7 网点位置编号Fig.7 Lattice point location number list

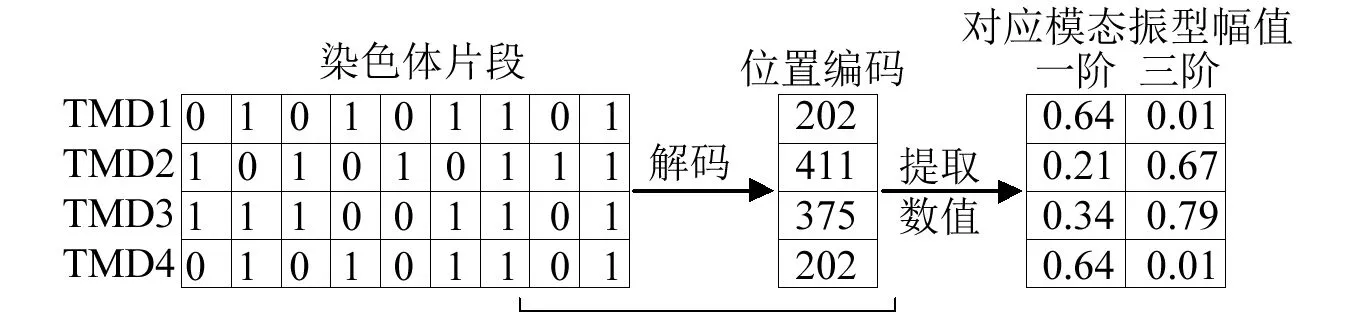
图8 单个个体的决策途径Fig.8 The approach of genetic algorithm individual expression

采用楼盖加速度为人体振动舒适度的衡量标准，定义楼盖结构舒适度控制的目标函数R，见式(7)，它是楼盖结构所有节点(式(7)中的k)在全部时间历程中(式(7)中的f)的最大加速度，同时为了保障体系的鲁棒性，降低楼盖结构面对参数摄动的风险，还应保证R值在所有可能的人类活动频段内(设定式(7)中f的取值范围为1.8～2.6 Hz)的数值最小。

(7)

运用遗传算法以式(7)为目标函数，选取楼盖一阶和三阶模态作为楼盖响应的叠加模态，结合式(6)计算结构响应，经过优化算法运算可得MTMD在给定参数下的最优安装位置。

2.3 MTMD位置与参数联合优化策略

为了实现MTMD位置和参数的联合优化，并保证优化过程的效率和稳定性，对遗传算法作以下补充，编写两个相互独立的优化进程，分别是“MTMD的位置优化进程”和“MTMD的参数优化进程”，每个优化进程单独对MTMD的位置或参数进行优化，都以R作为目标函数。在运算过程中两个进程交替运行，每个进程的输出结果都为下一个进程的初始条件，在联合优化过程中始终都是“已知位置求参数”与“已知参数求位置”的交替循环，避免了同时优化的不稳定性，提高了运算的效率，只需保证单个进程的精准性，就能保证整个运算策略的可靠性。图9为MTMD位置和参数联合优化策略。

在对MTMD进行联合优化时，输入一个初始的位置编号，将其代入“MTMD的参数优化进程”中，运算就的循环进行，通过设定循环次数，输出循环过程中的最优组合。

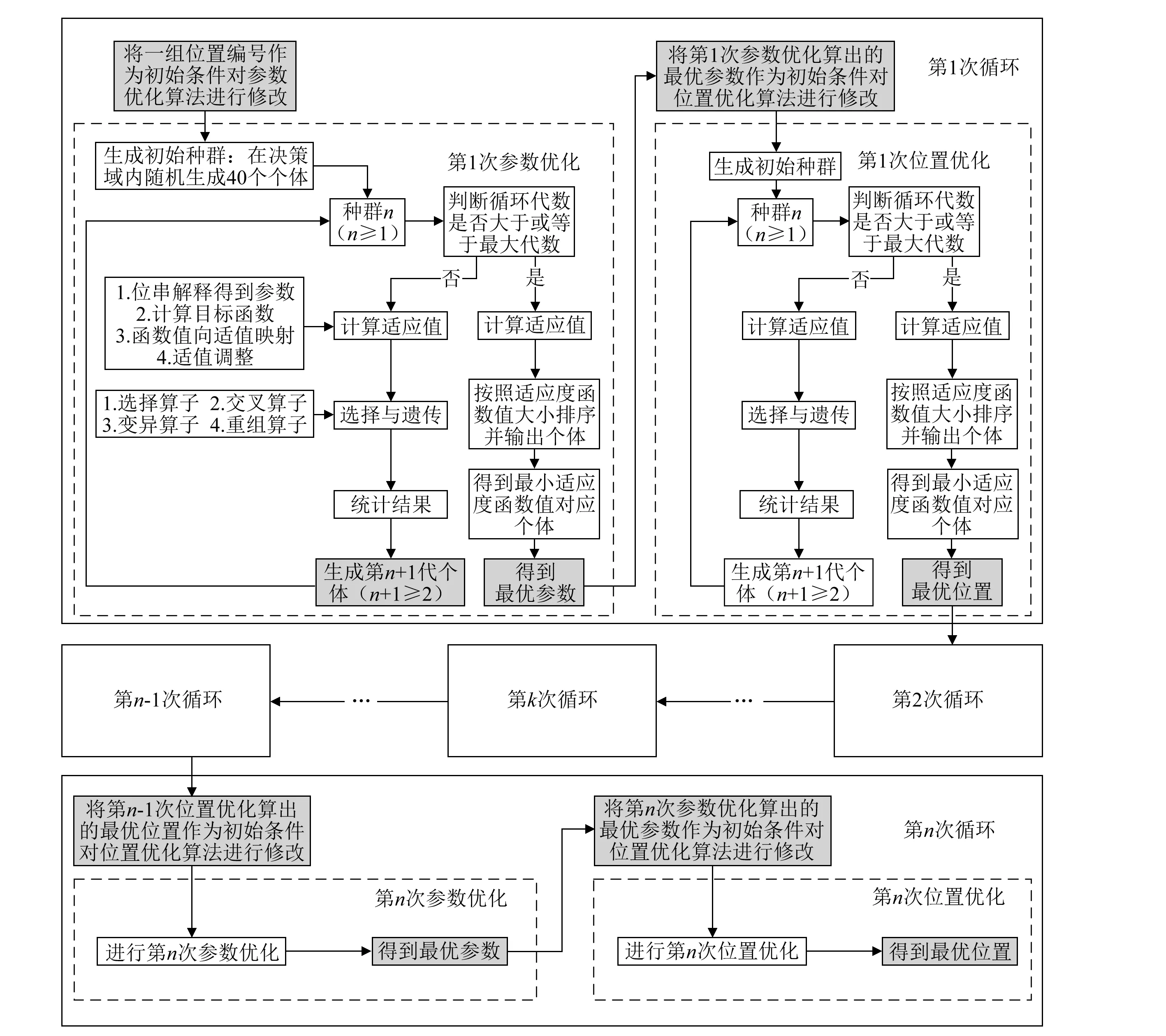
图9 MTMD位置与参数联合优化策略Fig.9 Combined optimal strategy of MTMD location and parameters

2.4 大跨度楼盖结构MTMD优化设计

利用联合优化策略对此张弦梁-混凝土板组合楼盖结构的减振系统进行优化。在“参数优化进程”中，TMD阻尼比取值范围设定为0.02～0.5，TMD频率的取值范围为1.58～4.73 Hz，由此构成参数优化的决策变量域；在“位置优化进程”中，TMD位置范围设定为图7所示的512个网点，由此构成位置优化决策变量域。人行荷载施加于楼盖跨中区域，等距间隔做同频率、同相位运动。考虑TMD组数对减振效果的影响，当组数过少时减振稳定性不能得到保障，当组数过多时MTMD制作不便，将组数设定为安装于不同位置的3组、4组、5组、6组的MTMD。

MTMD总质量的选取是优化过程需要考虑的因素，图10比较了不同质量比下的楼盖最大加速度。通过比较发现曲线拐点位于质量比为2%和3%处，不论质量比为2%和3%，都满足人体舒适度限制要求，从经济性角度来看，最终采用的MTMD总质量为18 000 kg(质量比2%)。

图10 不同MTMD质量比下楼盖最大加速度曲线Fig.10 Maximum acceleration curve of floor under different mass ratio

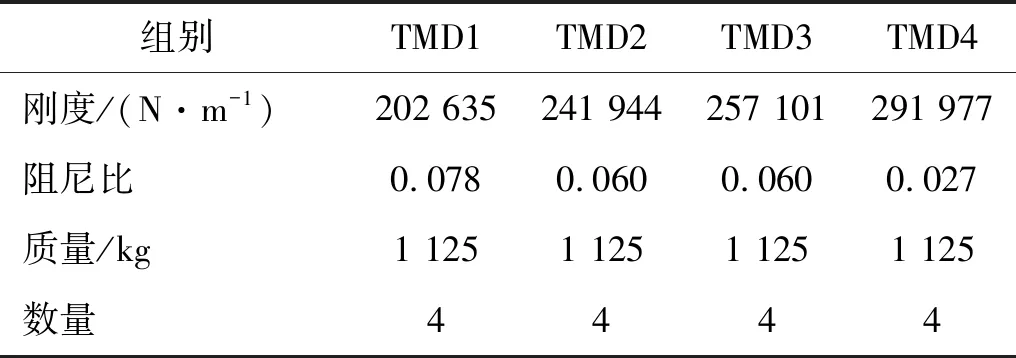
为与传统优化方法作比较，在进行联合优化前将初始位置编号设置成最大振型幅值处的位置编号，经联合优化得到了质量比为2%下各组参数和位置的最优组合(见表1)，因篇幅原因，仅绘制出各组在循环过程中产生最小R值的一次遗传优化过程(见图11)。

表1 各组TMD最优参数与最优位置Tab.1 Optimal parameters and locations for different number of TMDs

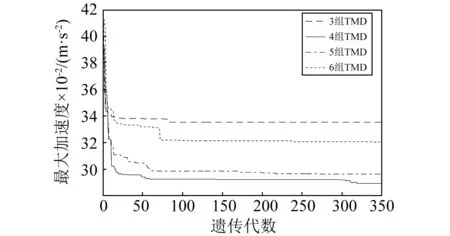
图11 不同组TMD遗传优化曲线Fig.11 Optimization curves for different number of TMDs

图12为曲线的起点是将MTMD布置于结构最大振型处(以下简称默认位置)只经过参数优化的楼盖最大加速度，从图12可知，随着循环次数的增加，楼盖最大加速度有不断下降的趋势，明显小于经传统优化后的最大加速度，可见经过联合优化后的MTMD减振效果得到了提升。由于TMD分组越多，安放位置越离散，MTMD组数越多减振效果未必更好。通过比较减振效果，采用图13布置位置的4组TMD，具体参数见表2。

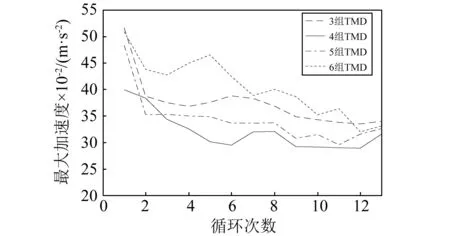
图12 不同组TMD联合优化曲线Fig.12 Combined optimal curves for different number of TMDs

图13 MTMD布置示意图Fig.13 Layout of MTMD used in the floor structure

组别TMD1TMD2TMD3TMD4刚度/(N·m-1)202 635241 944257 101291 977阻尼比0.0780.0600.0600.027质量/kg1 1251 1251 1251 125数量4444

定义减振率=(减振前响应-减振后响应)/减振后响应，定义提升率=(默认位置优化后响应-联合优化后响应)/默认位置优化后响应。通过表3可知，在结构最大振型幅值处安装MTMD有很好的减振效果，能够很大程度的缓解结构振动，减少约70%～80%的结构响应，通过位置与参数的联合优化，减振效果能够在此基础上进一步提升25%～40%。

由此可见，经联合优化后同等重量的MTMD能进一步发挥它的减振性能，较传统的优化方法优化后的MTMD减振能力得到了极大的提升。

表3 不同优化方式下楼盖最大加速度Tab.3 Maximum floor acceleration under different optimization methods

3 结 论

本文提出了一种MTMD位置优化方法，以此为基础制定了MTMD参数与位置联合优化策略，并用此策略对一个张弦梁-混凝土板组合楼盖结构的减振系统进行减振设计，减振效果明显，现得出如下结论：

(1)任何一阶模态响应都由全部TMD控制，它们以惯性力的方式作用在各阶模态上，通过振型幅值表现出不同的参与程度，在优化设计时需要考虑它们的协同作用。

(2)结合有限元法和振型分解法，以加速度响应为目标函数，以位置编号为决策变量，设计了一种MTMD的位置优化方法。

(3)MTMD参数与位置联合优化比传统的优化方法对MTMD减振效果的提升更大，可以将此方法运用于大跨度楼盖结构的减振设计中。