高中数学最值问题教学困境与突围之道分析

江苏省无锡市第三高级中学 高守家

数学最值问题存在于整个高中教材。通过了解实践教学案例可知，不管是三角函数，还是不等式、数列等模块包含的最值问题，都具有复杂性和多样性。因此，教师要想提升相关内容的教学效率，优化学生的解题水平，就要深层探索最值问题的解决方法，并对最值问题进行分类分析，以此针对不同类型的最值问题提出有效的解决方法。下面对高中数学最值问题进行研究。

一、二次函数的最值问题及解析

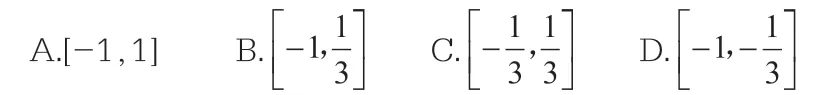
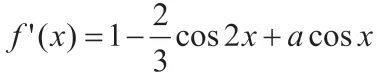
此时，令t=cosx,且t∈[-1，1]，

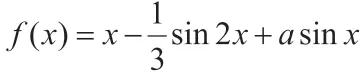
二、不等式的最值问题及解析

很多情况下，学生可以通过观察考试试卷发现，不等式恒成立问题一直都是他们学习的重难点，此时教师要想提升学生解题水平，减少问题的出现，要针对学生的薄弱环节进行分析。下面利用基本不等式分析求最值的技巧。例如，大部分学生会引用常数代换法进行问题解析，虽然这种方法操作起来非常简单，但会有一定误区，下面对例题进行分析：

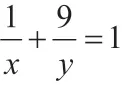
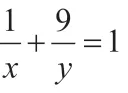
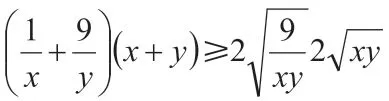
因此，最终可得x+y的最大值是12。

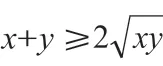
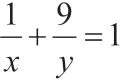
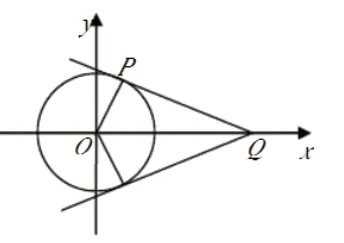
三、三角函数的最值问题及解析

对三角函数来说，教师结合自己的工作经验分析可知，可以引用多种方法解决其提出的最值问题，其中最常见的就是数形结合法。下面结合具体例题进行问题分析。

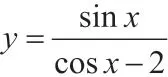
四、数列中的最值问题及解析

数列作为定义域是正整数的离散函数，不仅具备函数的性质，还拥有自己的独特性。高中教师整理以往教学经验可以发现，教师针对数列提出的最值问题主要分为三种：其一，求得数列的最大项和最小项；其二，求解等差数列的前n项和的最值；其三，数列中的恒成立问题。下面结合具体案例进行问题解析：

例4：已知数列{an}中，(n∈N+，a∈R，且a≠0)。

（1）若a=-7，求数列中最大项和最小项的值；

（2）若对任意n∈N+，都有an≤a6成立，求a的取值范围。

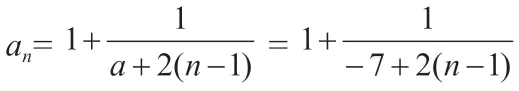
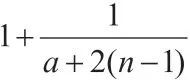
综上所述，为了让学生可以更快地理解和应用最值问题，高中数学教师要在引导学生解题的过程中强化他们的数学思维，并指导他们构建解题的自信心，进而依据引用科学的解题方法，帮助学生更快掌握和理解最值的有关知识点，以此在考试中获取优异成绩。同时，在新课改下，教师要调动学生自主探索的积极性，促使他们可以更快地计算最值问题。