数形结合思想在初中数学几何图形中的应用

江苏省苏州市汾湖高新技术产业开发区实验初级中学 陈 华

我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休。”可见，数与形存在着密切的联系性。从辩证法的角度来讲，数形结合思想是数与形之间的对立统一的关系。因此，在数学几何图形的教学中，教师采用数形结合的教学方法，将抽象数学语言与直观的图形结合起来，将复杂的问题简单化，从而优化解题思路，以培养学生的多维空间感和知识运用的能力。基于此，笔者将从“以数化形、以形变数、形数互变”三个角度来阐述数学结合思想在初中数学几何图形中的应用。

一、以数化形

由于数与形存在统一的关系，而以数化形的方法是指在数学学习的过程中，将抽象、难以理解的“数”通过具有形象、直观性的“形”表达出来。所以在教学初中数学有关几何图形的知识时，对于重点知识，教师依据数学结合思想，运用以数化形的解题思路和方法，遵循从简转化的基本原则，将问题中的数量转化为实际图形，并通过对图形的分析、推理，最终解决数量问题方法，从而让学生找出它们之间存在的内在联系，帮助学生找到解决问题的思路。

例如：在复习“圆”这一课内容时，为了让学生在解题中巩固对这部分知识点的掌握，我让学生运用以数化形的解题方法解析问题。比如：矩形ABCD的对角线AC、BD相交于点O，求证A、B、C、D四个点在以O为圆心的同一圆上。针对这一问题的解答，我让学生根据题中的已知条件，画出相应的矩形及对角线，以图形的直观性优势来求证圆的定理，并运用学过的知识有关圆的弦、半径的基本定理等，让学生依据画出的图形分析并解决问题。通过这样的方法，让学生掌握数形结合的基本思想，在解题中学会利用已知条件将“数”转化为“形”的解题思路。

二、以形变数

数与形之间还存在着对立的关系，以形变数就是数与形对立思维的直接体现。以形变数是指简单、直观的形需要借助数的形式来加以计算。因此，在几何图形问题的解题过程中，对于一些复杂的图形，教师要求学生养成善于观察图形的特点的习惯，进而充分利用几何图形的性质和意义，把形转换为数的形式，以便解答。另外，教师还要充分挖掘生活中的实例，从形到数，揭开藏身在“形”下“数”的面纱。

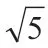
三、形数互变

形数互变是数与形对立统一辩证关系的最终形式，也是数形结合思想的核心。形数互变是指在数学问题的解答过程中，综合运用以数化形及以形变数的方法，从已知条件和结论出发，分析问题中存在的形数互变的内在联系。因此，在解析几何图形问题中，教师要逐步培养学生“由数想形——以形想数——数形转化”的思维，进而让学生能够在解析问题中掌握并灵活运用数形结合思想。

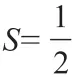
综上所述，数形结合思想在教学过程中主要表现为将抽象知识与直观的图形相结合，并让两者在一定条件下实现相互转化，是一种极具现代性的数学思维方法。随着新课程改革的不断落实，要求学生在数学学习过程中形成自己的数学思想和方法，用所学知识来解决实际生活中的问题。而数形结合思想在数学教学的应用中有助于开拓学生思路，对培养学生的数学核心素养也有着重要的推动作用。因此，作为一名优秀的数学教师，应转变教学理念，与时俱进，创新教学思路，以推动数学教学的发展。