借助几何画板对一道圆中问题的动态探究
王彬
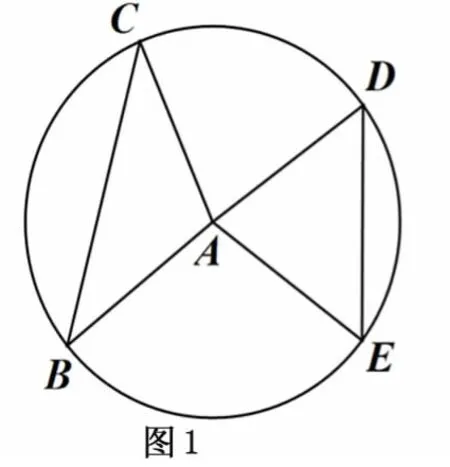
原题:如图1,在半径为5的⊙A中,弦BC,DE所对的圆心角分别是∠BAC,∠DAE,已知DE=6,∠BAC+∠DAE=180°,则圆心A到弦BC的距离等于多少?
这道题虽然是圆中的小题,但却是一道难题。已知条件给定了两个圆心角的和为180°,给定了其中一个圆心角所对的弦长,求圆心到另一条弦的距离。学生拿到题目后不容易想到从哪里入手。有弦能想到垂径定理,于是做辅助线,也只有作辅助线后才能把角度、弦和弦心距联系到一起,最终通过证明三角形全等得到所求的距离。

解法1:如图2,过点A分别向弦CB和弦DE作垂线,垂足分别为F、G

由圆中的关系定理可知在同圆中,圆心角、弦、弧、弦心距几个量中,只要有两个量相等,其余的各组量都相等。关系定理的证明是通过旋转证明的。也可以说在旋转的过程中,这几组量是不会变化的,那我们是否能用旋转其中一组圆心角和弦的办法让问题得到突破呢?能够想到旋转也是因为原题中有一个两角的和为180°的条件,而特殊角180°的出现,会让我们的问题另辟捷径吗?拭目以待。
解法2:如图3,当我们把∠BAC旋转使点B和点E重合。
∵∠BAC+∠DAE=180°
∴∠CAD=180°,即CD为直径
过点A作AF垂直于CE于F
由垂径定理可知,CF=FE
即,F为CE中点
又∵圆心A也是直径CD的中点
∴AF是△CDB的中位线


可以借助几何画板,快速直观解答,那么学生手中没有几何画板怎么解答呢?教师要借助几何画板培养学生动态分析和解决问题的能力。学生通过添加辅助线,把动态的最终结果呈现出来。
解法3:如图4,延长CA交圆A于点F,并连接BF
∵∠BAC+∠DAE=180°
又∵∠BAC+∠BAF=180°
∴∠DAE=∠BAF
∴BF=DE=6
过A作AG垂直于BC于G
则CG=BG
即G为CB的中点,又圆心A为CF的中点
∴AG是△CBF的中位线
几何画板在动态解决这道题的过程中,通过旋转使题目中位置关系和数量关系更直观,使原本复杂的问题变简单。但作为教师使用几何画板更重要的功能就是借助几何画板的动态演示、分析和求解的过程,培养学生动态分析和解决问题的能力。

