旋转行波超声电机最优预压力的研究

郭 咏，朱 华，刘 军，赵淳生

(南京航空航天大学 机械结构力学及控制国家重点实验室，江苏 南京 210016)

0 引言

旋转行波超声电机是一种利用压电陶瓷逆压电效应使定子产生微幅高频振动，再通过定、转子间的摩擦来驱动转子并带载的微特电机[1-2]。为使定、转子接触面形成有效的摩擦副，须在接触界面的法向施加正压力，即超声电机预压力(F)。预压力决定了定、转子的接触状态，影响超声电机系统的能量传递过程，是电机机械特性的重要影响因素[3]，因此,许多学者从理论和实验上对超声电机预压力进行了研究。文献[4-5]建立了行波超声电机的三维摩擦驱动模型, 认为接触界面作用力存在轴向、周向和径向分量，分析了预压力影响电机性能的原因。文献[6-9]通过有限元仿真和实验研究了超声电机摩擦层在预压力下的变形规律，分析了不同预压力下定、转子的接触状态及预压力对行波超声电机空载转速、堵转力矩等指标的影响。文献[4-9]普遍认为，过大或过小的预压力均不利于超声电机的运行，超声电机工作存在最优预压力；当激励不变时，超声电机在最优预压力下输出效率最高，输出功率最大。

实践中发现，旋转行波超声电机最优预压力值不仅与电机自身设计参数有关，也受负载力矩的影响。目前超声电机在装配时，预压力通常采用固定值，而非根据实际负载需求进行设定。若预压力的设定值偏离实际负载下的最优预压力，将导致电机输出性能下降。本文在旋转行波超声电机定、转子二维接触模型[10]基础上，分析预压力对超声电机机械特性的影响，进而得出超声电机最优预压力与负载的关系，并通过实验进行了验证。研究结果为已知负载下的超声电机预压力的选用提供了理论依据，也为作者后续研制自适应预压力超声电机提供了支撑。

1 最优预压力的推算

研究超声电机最优预压力，首先分析预压力对电机机械特性的影响。预压力对超声电机的影响包括对定子振幅，定、转子接触范围及等速点位置的影响[5]，这些因素最终决定了超声电机的输出性能。以TRUM-70H旋转行波超声电机为研究对象分别对三者进行分析，并推算不同负载下电机的最优预压力。

1.1 预压力对定子振幅的影响

旋转行波超声电机定子的动力学方程为

(1)

式中：Ms、Cs、Ks分别为定子的模态质量、阻尼和模态刚度；y为定子中性面位移；Δ为机电耦合系数，反映系统将电激励转换为机械响应的能力；V为激励电压；Fn为接触界面对定子的反作用力，与预压力正相关。由式(1)可见，当预压力增大时，接触界面对定子约束加强，定子振幅(A)下降。但是，定子结构较复杂，物理参数不易确定，很难通过解析法准确计算其振幅，故采用实验测定。利用德国Polytec公司PSV-300F-B型高频扫描激光测振系统，在峰值电压为200 V单相正弦激励下，测定TRUM-70H超声电机定子振幅与预压力的关系。实验中，由透明压板施加预压力，其值通过预压力螺母进行调节。扫描激光点透过透明压板至定子上表面反射，并由此测得定子表面质点振幅。图1为带预压力定子测振工装，表1为测试结果。

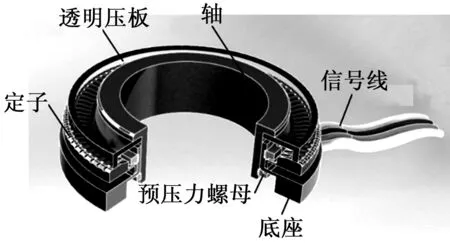
图1 带预压力定子测振工装

F/N0300400500600700频率f/kHz49.752.253.754.055.356.8A/μm1.60.570.500.450.410.36

由表1可见，随着F的增加，A逐渐降低，而谐振频率升高。为方便下文计算，根据表1测振数据，F=300～700 N时,定子表面质点A与F的数值关系近似拟合为

A=c·F-m

(2)

式中c，m为常数。

1.2 预压力对接触范围的影响

将旋转行波超声电机定、转子接触界面沿周向二维展开，如图2所示。当定子被激振时，其表面呈正弦波状，波峰两侧在(-θ0，θ0)区间内与转子摩擦层接触，而以外部分则相互脱离[11]。图中，θ0为摩擦层与定子接触的临界位置，θs为等速点，E为摩擦层材料的弹性模量，za为摩擦层厚度，z0为转子基体纵向位移，Td为驱动力矩，Tr为阻碍力矩，v为转子运行速度方向。

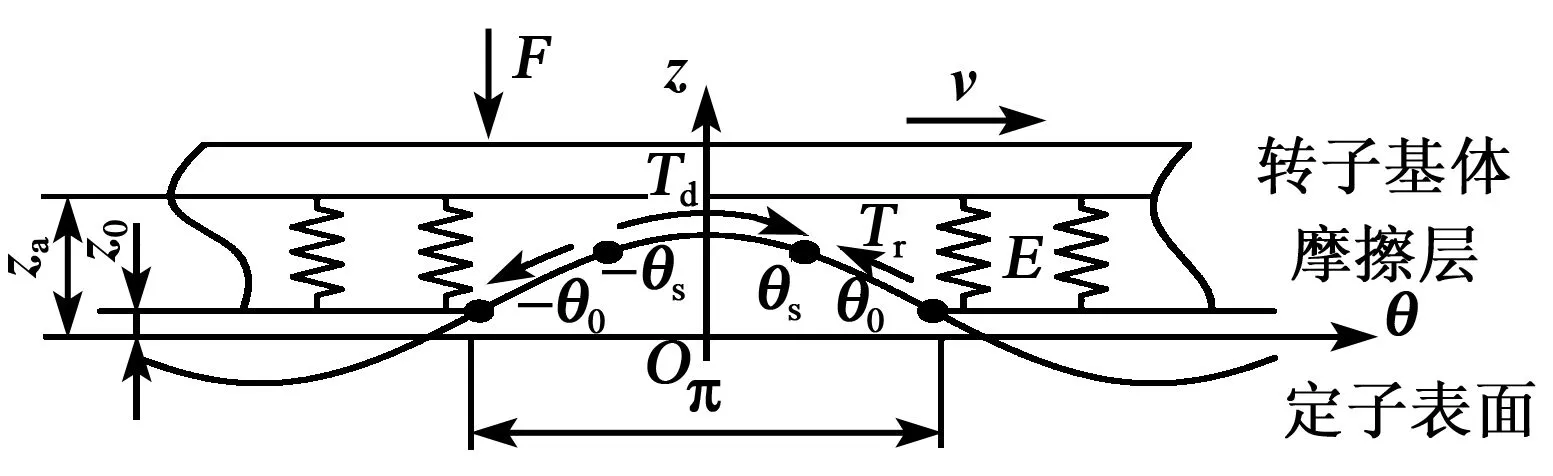
图2 接触界面周向展开

TRUM-70H超声电机摩擦层厚为0.25 mm，而定子振幅仅为1 μm量级，可认为电机工作中摩擦层始终为弹性形变，定子表面任意质点处正应力与该点摩擦层应变成正比[12]。根据1.1节的测振结果，定子表面轮廓在预压力下基本保持正弦状，则接触界面θ处摩擦层形变量为

δ(θ)=Acosθ-z0

(3)

由胡克定律，接触界面θ处的纵向正应力为

σz(θ)=Eδ(θ)/za

(4)

在纵向，转子受到向下的预压力和向上的接触界面作用力，由二力平衡得

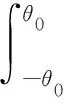
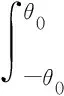
(5)

式中：n为定子模态节径数，即旋转行波一周的波峰数;r为接触界面沿径向的宽度。若θ0处摩擦层形变量恰好为0，则有

δ(θ0)=Acosθ0-z0=0

(6)

将式(2)、(6)代入式(5)，积分得

F1+m=2cnEr/za·(sinθ0-θ0cosθ0)

(7)

1.3 预压力、负载对等速点的影响

定子表面质点的周向速度不等，波峰处最高，两侧逐渐降低；而转子上各点速度近似相等，介于定子波峰与节点(周向速度为0)之间。因此，在接触区域内存在定、转子周向速度恰好相等的点，称为等速点θs。由图2可知，等速点对称分布于波峰两侧。在(-θs,θs)区间内，定子表面质点周向速度大于转子，对转子起摩擦驱动作用，产生Td；在(-θ0,-θs)和(θs,θ0)区间内，定子表面质点周向速度小于转子，对转子起摩擦阻碍作用，产生Tr[13]。因此,转子周向运动方程为

(8)

Td-Tr-Tl=0

(9)

假设定、转子间滑动摩擦力与接触界面正压力的关系满足库仑摩擦定律，则

(10)

式中:μd为摩擦系数；R为接触界面等效半径。

将式(4)、(10)代入式(9)，积分得

2sinθs-2θscosθ0+θ0cosθ0-sinθ0=

(11)

1.4 最优预压力与负载的关系

最优预压力即激励不变时，在一定负载下使超声电机获得最高效率和最大输出功率的预压力。当负载一定时，电机输出功率最大,即转速最大。根据超声电机在不同预压力下转速的变化，可寻得最优预压力点。根据文献[1]，定子上表面质点的切向速度沿周向呈余弦分布，最大速度在波峰处，其值为

(12)

式中:h为定子中性面至上表面的距离；ωn为驱动信号圆频率。结合1.3节，转子转速等于θs处的定子表面质点切向速度，因此,电机转速为

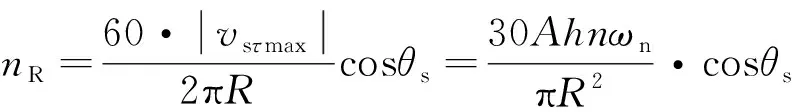
(13)

联立式(7)、(11)、(13)可得

(14)

式(14)反映了超声电机转速与预压力及负载的函数关系，构成了超声电机运动的简化数学模型，其相关参数如表2所示,表中参数的研究对象为TRUM-70H超声电机。

表2 计算参数

利用MATLAB对式(14)求数值解，得到不同负载下超声电机转速与预压力的关系，如图3所示。

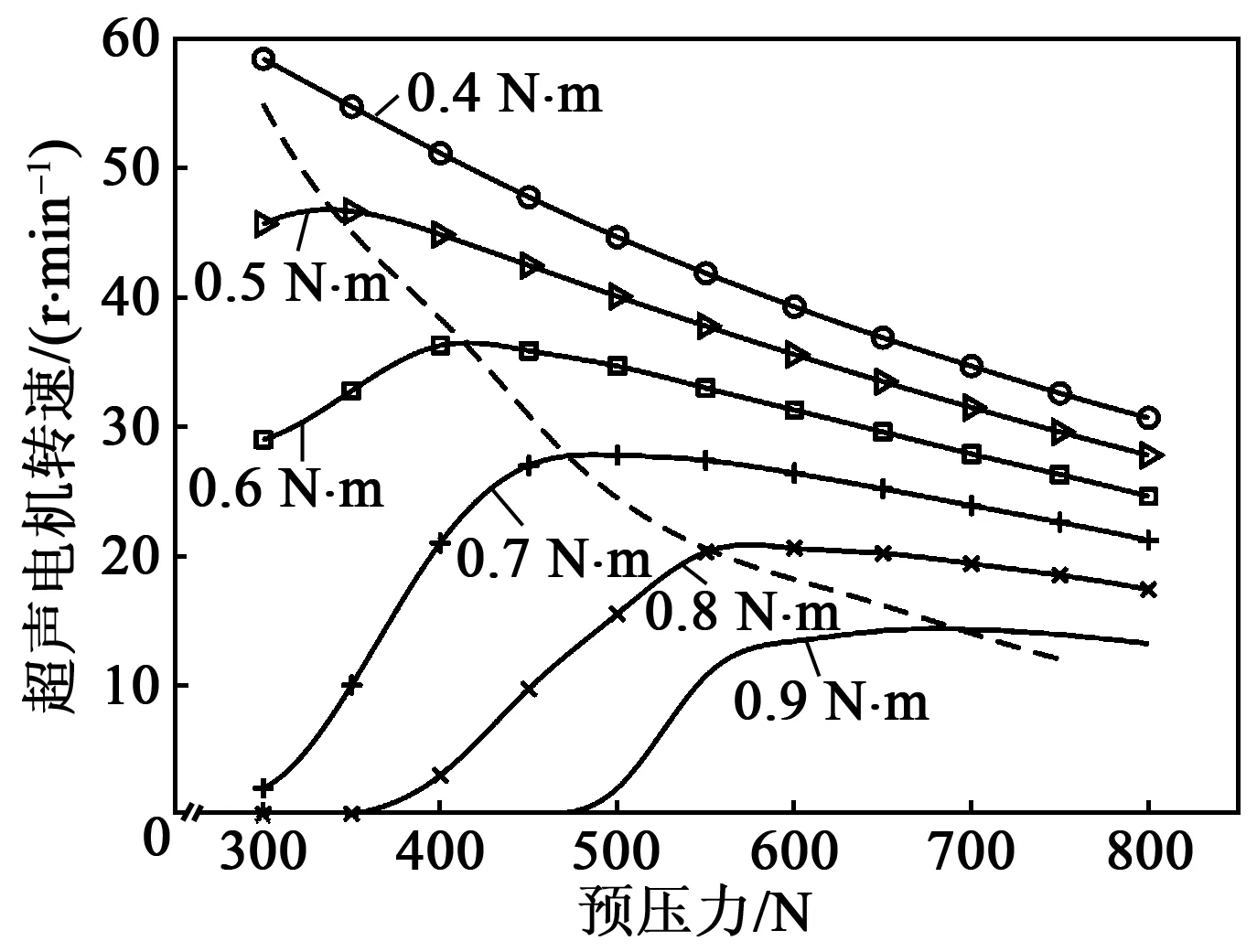
图3 不同负载下转速与预压力的关系(模型计算)

在任一负载下，随着预压力的增大，超声电机转速先增大后减小，各条曲线极值点处的预压力即为该负载下超声电机的最优预压力。图3中虚线反映了负载力矩从0.4 N·m增加到0.9 N·m过程中，超声电机最优预压力从约300 N逐渐增加到约700 N。

2 实验研究

2.1 实验验证及误差分析

为验证上述最优预压力与负载的关系，搭建的超声电机多功能测试平台如图4所示，包括负载施加与反馈、预压力施加与反馈、速度反馈三项功能。其中，负载施加模块依靠加载电机推动丝杠螺母沿轴向运动，压缩弹簧产生轴向正压力，进而使摩擦片与挡板间产生可调节的摩擦力矩作为模拟负载；预压力施加模块是依靠电磁铁对衔铁产生吸合力，通过轴向传递作用在定、转子接触面上，为被测超声电机提供可控的预压力。负载力矩、预压力、电机转速的数值分别通过力矩传感器、力传感器和编码器进行显示和反馈。

图4 超声电机多功能测试平台

利用该试验台对两相峰值电压200 V、51 kHz正弦激励下的TRUM-70H超声电机进行测试，得到不同负载下转速与预压力的关系，如图5所示。将图3及图5中虚线反映的最优预压力随负载的变化进行规律整理，如图6所示。由图6可见，在超声电机有效工作范围内，最优预压力与负载力矩近似线性正相关。因此，在超声电机装配时应根据实际负载需求选用对应的最优预压力，对于大负载应采用较大的预压力，反之则采用较小的预压力。

图5 不同负载下转速与预压力的关系(实验数据)

图6 最优预压力与负载的关系

图6中计算与实验数据曲线的总体趋势一致，但在负载力矩较低的部分两者误差偏大，实验中被测超声电机在低预压力下带小负载时的转速低于模型预期，小负载工况下的最优预压力高于模型预期。这是因为当预压力较小时，转子的纵向约束减少，定子的振动不能被摩擦层有效吸收，部分能量转化为转子基体无效的纵向振动[13]，转子基体上质点的运动由近似水平圆周运动转变为波浪式起伏的圆周运动。此时,定、转子接触界面不再是一个仅在水平方向旋转的形状固定的空间曲面，等速点理论不再适用。因此,在低预压力下，由于转子存在高频纵向振动，超声电机的噪声显著增大，而输出功率和效率则明显下降，使得小负载工况下的最优预压力高于模型计算值。

2.2 自适应预压力下超声电机机械特性

考虑到在一些场合下电机的负载是变化的，无法在装配时根据确定的负载需求选用最优预压力。这种情况下若超声电机预压力能随负载的变化而自适应调整，则可使电机在各工况下的输出性能均保持最优。仍利用图4的超声电机多功能测试平台，分别在500 N预压力和自适应预压力下对TRUM-70H超声电机进行测试，激励电压峰-峰值为200 V，驱动频率为51 kHz。两者的机械特性曲线对比图如图7所示。

图7 两种预压力下超声电机机械特性对比

由图7可知，超声电机在自适应预压力下的机械特性曲线始终在500 N固定预压力的曲线上方，空载转速更高且堵转力矩更大。因此，如果超声电机预压力不再设定为固定值，而是随负载变化自适应调整，则其输出性能可进一步提升。作者后续将据此研制一种自适应预压力的超声电机，采用电磁力替代常规的螺纹预紧力为电机提供预压力，预压力的大小通过线圈电流控制，并通过负载力矩进行反馈。

3 结论

1) 建立旋转行波超声电机力学模型，基于测振试验和等速点理论，说明超声电机运行存在最优预压力，并推导得出最优预压力与负载的关系。

2) 搭建超声电机多功能测试平台，对TRUM-70H超声电机进行测试。实验结果验证了理论推导，指出在超声电机有效工作范围内，最优预压力与负载力矩近似线性正相关。同时解释了计算与实验存在误差的原因是预压力较低时等速点理论不适用。

3) 提出了为提高超声电机输出性能，在装配时应根据实际负载需求选用对应的最优预压力，对于大负载应采用较大的预压力，反之则采用较小的预压力。

4) 测试了超声电机在自适应预压力下的特性曲线，并与常规的固定值预压力电机机械特性进行对比，验证了超声电机工作在最优预压力下的优越性，为下一阶段研制自适应预压力的超声电机提供支撑。