“构造逆命题”在初中几何图形的判定教学中的应用

江苏省昆山市城北中学 金小丹

数学学习中，处处有命题，在很多情况下，我们可以通过对调原命题的条件和结论来构造原命题的逆命题，从而获得新知识。初中几何中同一知识对象的性质定理与判定定理往往是互逆的，如平行线的性质与判定、平行四边形的性质与判定等。本文就几何图形判定定理的教学为例做分析，探讨如何利用矩形、菱形的性质定理构造逆命题来学习矩形、菱形的判定定理。以此为基础，结合“直角三角形斜边上的中线等于斜边的一半”的逆命题阐述如何引导学生获得新知。

一、从矩形、菱形的性质定理到矩形、菱形的判定定理

学习矩形、菱形的判定定理前，学生已经学习了性质定理，因此，可以将性质定理确定为新知识的生长点，引导学生逆过来思考，即构造性质定理的逆命题，加以证明或修正，从而主动获得矩形、菱形的判定定理。

先以矩形判定定理教学为例，学生已经学习了矩形的性质定理——矩形的四个角都是直角，对角线相等。上课之初，我让学生分别写出以上两个命题的逆命题——“四个角都是直角的四边形是矩形”“对角线相等的四边形是矩形”。

对于第一个命题，“四个角都是直角的四边形是矩形”，这是真命题。我引导学生思考是否需要四个角都是直角，学生意识到存在多余条件，可以修改为 “三个角都是直角的四边形是矩形”，接着画出图形，运用矩形的定义进行证明。

已知：在四边形ABCD中，∠A＝∠B＝∠D＝90°，求证：四边形ABCD是矩形。

证明：∵∠A＝∠B＝∠D＝90°，

∴∠A+∠B＝180°，∠A+∠D＝180°，

∴AD∥BC，AB∥DC，

∴四边形ABCD是平行四边形，

又∵∠A＝90°，∴四边形ABCD是矩形。

经过证明，这个命题是真命题，于是得到判定定理——“三个角是直角的四边形是矩形”。

对于第二个命题，“对角线相等的四边形是矩形”，学生很快判断这是个假命题，并且举出反例——等腰梯形。接下来自然产生疑问：“这个命题如何修改可以得到一个真命题？”经过短暂思考，学生给出答案，将“四边形”改为“平行四边形”，即“对角线相等的平行四边形是矩形”。

在根据矩形的定义证明这个命题时，学生提出可以通过三对边对应相等证明图中△ABD与△DCA全等，从而得到∠BAD与∠CDA的等量关系，又由平行四边形对边平行可得AB∥DC，从而∠BAD与∠CDA互补，因此∠BAD与∠CDA都等于90°，根据矩形的定义可证得四边形ABCD是矩形。具体证明过程如下：

已知：如图1，在ABCD中，AC=BD。求证：ABCD是矩形。

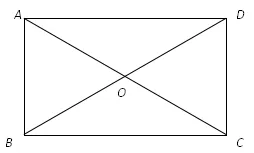
图1

证明：∵四边形ABCD是平行四边形，

∴AB∥DC，AB=DC。

∵AB=DC，AD=AD,BD=AC，

∴△ABD与≌△DCA（SSS）。

∴∠BAD=∠CDA。

∵AB∥DC，∴∠BAD+∠CDA＝180°，

∴∠BAD=∠CDA=90°，∴平行四边形ABCD是矩形。

经过证明，这个命题是真命题，于是得到判定定理——“对角线相等的平行四边形是矩形”。在探索矩形的判定定理教学过程中，以学生已有的矩形的性质为知识生长点，通过构造逆命题来获得矩形的判定定理，这符合新的建构主义思想：教学应当把学习者原有的知识经验作为新知识的生长点，引导学习者从原有的知识经验中生长新的知识经验。

学习菱形的判定方法时，同样的方法，让学生写出菱形的两个性质“菱形的四条边相等，对角线互相垂直”的逆命题，进而通过证明命题或者对命题进行修改使之成为真命题，从而得到菱形的判定定理“四边相等的四边形是菱形”“对角线互相垂直的平行四边形是菱形”。

因为探索矩形或菱形的判定方法是建立在学生已有的知识经验基础之上的，学生对于矩形、菱形的性质并不陌生，只是将性质定理改写为逆命题并合理修改并证明，使之成为真命题，所以整个教学过程都是在教师的引导下自然进行的，学生积极参与到学习中来，凸显了学生的主体地位，做到了“将课堂还给学生”。

二、从直角三角形斜边中线定理到逆命题

直角三角形是初中几何中一种重要的图形，斜边上的中线定理是常考常用的一个定理。这个定理没有逆定理，但是它的逆命题在判断一个三角形的形状时会经常出现，因此，在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后，我让学生写出这个命题的逆命题“在一个三角形中，如果一条边上的中线等于这条边的一半，那么这个三角形是直角三角形”并判断其真假。

学生通过举例猜想这是个真命题，之后通过几何证明验证了猜想。

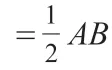
图2

分析：要证明∠ACB＝90°，就是要证明∠ACD+∠BCD＝90°。由条件可知AD=BD=CD，则∠A＝∠ACD,∠B＝∠BCD，所以∠ACD+∠BCD= 内角和的一半。

证明：在△ABC中，

∵CD是AB边上的中线，∴AD=BD=AB。

∵CD＝AB，∴AD=BD=CD，

∴∠A＝∠ACD,∠B＝∠BCD，

∵∠A+∠ACD+∠B+∠BCD=180°，

∴∠ACD+∠BCD=90°，

即∠ACB＝90°，∴△ABC是直角三角形。

经过证明，学生对这个命题有了深入的领悟，之后通过系列练习，学生提出 “如果一个三角形一边上的中线将这个三角形分成了两个等腰三角形，那么这个三角形是等腰三角形”也是个真命题。

三、小结与思考

数学学习中处处有命题，处处有新知，“授人以鱼不如授人以渔”，如何发挥学生的自主性，主动获得新知识，这是每位教育工作者都会思考的问题。学生的知识体系是不断充实的，如果能利用学生已有的知识体系，找准知识生长点，加以适当的引导，让学生自主学习，将起到事半功倍的效果。