如何培养学生高中数学直观想象能力

黄旭明

(福建省福安市第三中学 355002)

直观的本质就是在直接接触客观事物的过程中所产生的感性认识，而想象的本质是在人类大脑之中对已经存在的表象予以加工而产生了一种新形象的一种心理过程.数学直观想象力就是在几何直观与空间想象当中，去对事物的变化和基本形态进行感知，最后通过对图形的理解来解决一些数学问题.它是数学核心素养的重要组成部分之一，在数学教学当中直观想象有三种基本表现形式，即利用图形构建直观模型、运用图形理解数学问题、利用图形解决数学问题.能够看出来，不论是哪一种表现形式都无法脱离图形而存在，因此这就需要教师在教学的过程中加大对学生作图与识图能力的培养.

一、通过数形联系，培养图形运用能力

直观想象的本质就是通过对图形进行理解，以此来解决一些数学问题.在高中数学之中，数与形之间有着密不可分的联系，将这两者的联系建立起来，可以有效促进学生对问题的认知与理解，进而快速寻找到解决问题的方式.“数缺形少直观，形缺数难入微.”通过数形结合的方式解决数学问题，不但要让学生将原本抽象的题目直观化，还应该要加大对学生图形洞察力的培养，使其可以依照图形之中的已知信息对结论进行直观推理，然后获得解题思路，提升直观想象核心素养.

在高中数学之中向量一直以来都是非常重要的一项考察点，它不仅具有代数的抽象性和严谨性，同时还具备几何的直观性.因此在各大考试过程中都尤为重视学生对向量运算法则的掌握情况和对几何意义的理解.如果在教授向量的时候，可以引导大家先将向量的本质认识清楚，并学会运用图形去解决一些问题，除了可以缩减学生解题的时间之外，还能够培养起来学生的直观想象力，进而提升大家运用图形的能力.

例1 已知|a|=|b|=1,a·b=0,且|c-a-b|=1,那么|c|的最大值为____.

解析由于向量本身就是数形相互结合发展出来的，那么在解决这类问题的时候就需要将向量加减法的基本几何意义把握住，然后再通过图形，将向量几何的直观性完全呈现出来，以此来有效解决问题.

对于这一道例题来说，在解答的时候就可以依照这一思路进行.具体：

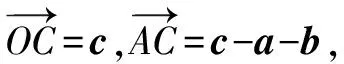
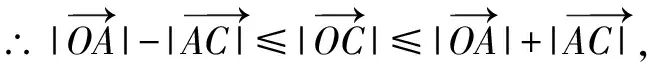
图1

通过这一例题分析之后能够让学生对向量加法与减法存在的几何意义有更深一步的理解，并且还可以让大家能够感受到通过对图形的认识便能够快速解决一些数学问题，进而有利于培养大家的直观想象力，从而提升图形运用的能力.

二、通过模型，培养空间思维

教师在教学的时候还需要重点引导大家通过构造直观模型解决一些数学问题，一般构造的直观模型主要包含有立体几何、解析几何以及平面几何.在立体几何当中主要包含有四面体及长方体等等；在解析几何模型之中主要是点与线之间的距离、点与点之间的距离、圆锥曲线、斜率等等；在平面几何之中主要包含有三角形、圆等.这种直接将数学问题直观化的模式能够促进对问题的推理及把握，进而简化数学问题.这也是目前培养直观想象核心素养最有效的一项途径.

比如，在高中数学教材当中，立体几何与几何模型的制作有着极为密切的联系，所以在教授这节内容的时候就需要引导学生们加强对模型的观察，并让大家在制作模型的过程中加强对数学问题的思考.在解答立体几何的过程中，可以将一些特殊模型运用进去，例如长方体或者正方体等，就可以让大家直观感受到这些模型之中点线面所存在的基本位置关系，从而就可以积累出来立体几何的表象，提升对立体图形的直观感，最后养成空间思维的基本能力，这对于培养学生直观想象力同样也具备一定的积极意义.

例2 (见2014年全国卷)如图2，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( ).

图2

通过对这一例题的基本解读能够发现，它主要是要求学生将三视图还原成为一个几何体，然后在其中找到最长的棱.这类题目在各大考试当中非常常见，通常会对学生的想象力和空间思维能力提出较高的要求，因此大部分人都不会做.如果在教学的时候，将特殊模型运用进去，让学生将模型的正、俯、侧三个视图分别当作几何体在模型之中里、底与右侧三面的投影，就可以有效增强题目的直观性，进而激发学生的空间想象力.以后学生在遇到类似题目无法有效还原的时候，还可以让大家在特殊模型之中将几何体的顶点确定出来，最终将几何体还原出来.

就例2来讲，就可以完全选择一个棱长是4的正方体，从其俯视图当中就可以得知，其顶点是不会出现在A点和A1点的，也就是可以直接将这两个顶点排除掉，借用相同的理由在正视图当中还能够再将A点与D点排除掉；又在侧视图当中将B点与B1点排除掉，那么剩下的三个顶点就会成为几何体的顶点，接下来再依照正视图就能够将三棱锥的第四个顶点确定出来，即棱BB1的中点E.所以最后的几何体就是E-CC1D1，最长的一条棱就是ED1,其长度为6.

在培养学生直观想象力的过程中，运用空间几何体的三视图可以起到事半功倍的效果，并且在特殊模型的作用下，还可以有效提升大家的直观感受，并给想象力的发挥创设更广阔的空间，进而整个解题过程变得更加迅速和便捷，最后提升学生的直观想象力.

三、通过图象特征理解，培养数形结合

在高中数学学习过程之中函数是非常关键的一项研究对象，其图象基本的几何特征可以将函数的基本性质有效展现出来，另外借助于图象还能够迅速找到解决问题的方式.在培养直观想象力的过程中直观洞察力是非常显著的一项特征，它的本质就是人类在获得既定情境图象的基本信息之后，可以将这些信息和自己已经具备的知识体系相互联系起来，并从中将解决问题的能力筛选出来.所以能够发现，让学生将基本初等函数的基本图象特点和一些较为常见的图形变换掌握并完全理解，可以有效促进在解题方面的洞察力，最终提升直观想象力，与此同时运用得当还能够反过来促使数形结合能力得以提升.

例3 若函数f(x)的定义域是R，其图象关于原点对称，当x>0时,f(x)=x3-2，那么函数f(x+2)全部的零点和是( ).

通过对上述例题的初步分析能够发现，这重点是考察求函数图象的基本性质，其中f(x)是奇函数，所以这就能够发现，当x>0的话，那么其函数f(x)的解析式就能够轻易得到，同理f(x+2)的解析式也能够获得，最后就可以将所有零点的和解出来.但是这道题目如果使用这种方式直接进行解答的话，那么整体计算量相对就会比较大，所以这就可以将其奇偶函数的基本性质结合进去，站在函数图象变换的角度上来解答这一例题就能够迅速得到答案.

解析由题目可以得知f(x)是奇函数，当其x>0的时候，f(x)=x3-2.

通过图象可以获得(图3)，f(x)存在一个大于0的零点，即x1(x1>0)；再从其奇函数的基本性质能够得到，f(x)存在一个小于0的零点，即x2(x2<0)，并且这两个零点都是关于原点对称的，再从其函数性质能够获得f(0)=0，也就是其函数零点x3=0.

图3 图4

将其f(x)的图象向左面平移两个单位就可以获得f(x+2)的图象(图4)，将其f(x)的零点向左面平移两个单位可以获得f(x+2)的零点，并且其零点x4与x5是关于(-2,0)对称的，而x6=-2，所以最终就能够获得f(x+2)的全部零点和就是-6.

在解决上述的例题的时候，将学生比较熟悉的图象平移变换以及对称等相应的知识内容应用进去，就可以及时获得题目之中的一些特定信息，由此就可以再依照直观洞察力直接获得最终题目的答案.总结来说，图象的基本特点和变换是培养直观洞察力的重要基础，教师在上课的时候除了要让大家可以精准地观察并绘制图形之外，还要让大家尽量掌握函数之中图象的基本变换情况，这样一来不但可以提升学生的直观洞察能力，培养直观想象力，还能够反过来促进数形结合能力的提升.

总的来说，在教学的时候培养大家的直观想象力其本质就在于培养大家通过数学视角去观察和理解世界，并通过相应的方式，以图形、模型和图象为载体，促进学生运用图形能力的提升，并进一步培养基本的空间想象力.这样一来不但能够直接简化一些数学问题，还能够促进大家创新思维的提升，进而发展起来基本的直观核心素养.