不回避 不惧怕
——高中物理关于微积分的教与学
王 娟
(江苏省淮安市淮阴中学 223002)
一、物理课堂内外关于微积分教与学的现状
1.教材编写者回避
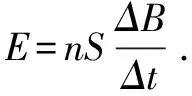
2.高考命题者回避
近几年出现了大量的可以利用微积分来解决问题的高考题和高考模拟题,但是在具有指挥棒作用的高考试卷的参考答案中我们却没有看到利用微积分这种简单方法来求解的答案,而更多的是利用微元求和的思想来处理,这对中学物理微积分的教学也起到一定的阻碍作用,因此教师在课堂上不太愿意也不太敢用微积分的方法去解决问题.
3.学生关于微积分的学习是雾里看花
对于微积分初步知识的学习,数学和物理都有所涉及,但都没有做出具体的要求,学生所能达到的程度仅限于一知半解,因此在应用微积分知识去解决物理问题时只能是雾里看花.
二、现行中学阶段微积分教学有效策略的研究
1.教学时间安排
在高一,物理必修1和必修2中出现了15处体现微积分思想的内容,到了高二,学生在数学教材中系统的学习了微积分的初步知识,但这两者在很多学生的头脑里还是两条平行线,还不能做到将数理进行整合与优化.到了高三物理第一轮复习前我们可以将这两者进行有机的整合,适度地应用微积分,深化已学过的物理概念,拓展解题思路,优化解题过程.
2.理解并熟记常用的求导和积分公式
(1)常用的求导公式
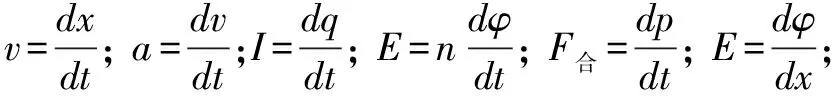
(2)常用的积分公式
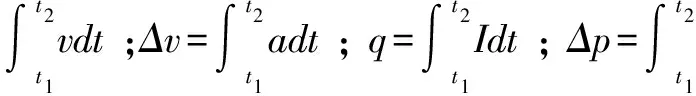
三、利用微积分知识处理高中物理问题实例分析
1.求导方法的应用实例
导数在物理里的应用实质上是将物理内容结合到它的几何意义中.导数在求解切线斜率和极值时具有比较简单方便等优势,因此以后碰到这类问题时,我们可以试着用导数来解决.
(1)利用导数结合物理图象对物理量的变化进行判断
例题真空中有一半径为r0的带电金属球壳,通过其球心的一直线上各点的电势φ分布如图1所示,r表示该直线上某点到球心的距离,r1、r2分别是该直线上A、B两点离球心的距离.下列关于A、B两点电场强度大小判断正确的是(A).
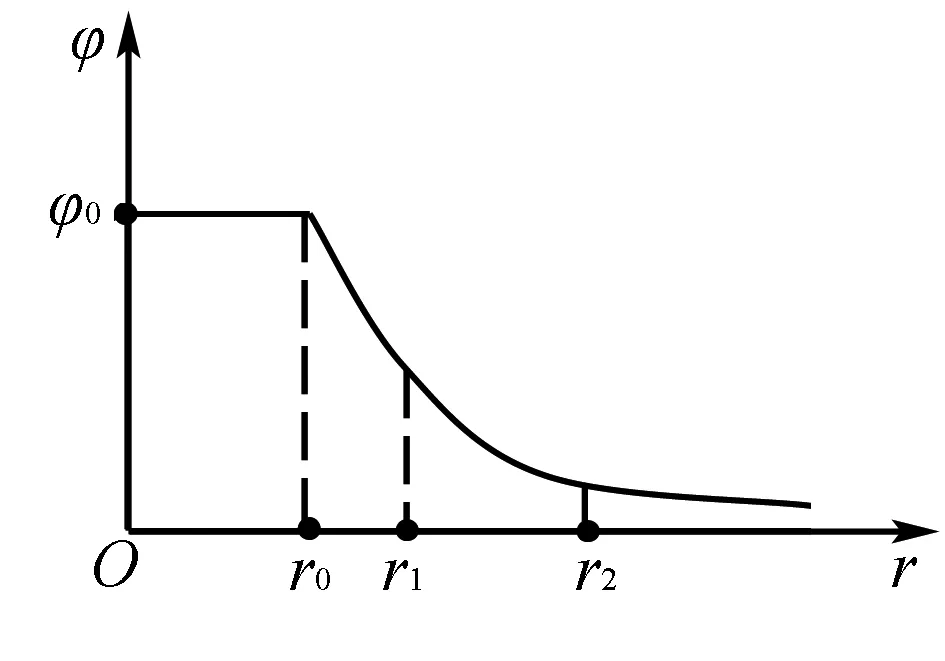
图1
A.EA>EB
B.EA=EB
C.EA D.不确定 强度的大小. (2)利用导数结合数学方法求解物理量的极值 例如求某一物体在运动过程中加速度的最大值,其加速度的表达式为: 发现加速度是一个关于θ的函数,令f(θ)=sinθ-sin3θ 令f′(θ)=0,即cosθ-3sin2θcosθ=0 2.积分方法的应用实例 积分在高中物理中的应用分为两类,一类是直接利用物理意义积分,另一类是利用数学方法积分. (1)直接利用物理意义积分 图2 例题如图2所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a (2)利用数学方法积分 图3 例题如图3所示,两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上,两导轨间距L=1m,导轨的电阻可忽略.M、P两点间接有阻值为R的电阻.一根质量m=1kg、电阻r=0.2Ω的均匀直金属杆ab放在两导轨上,与导轨垂直且接触良好.整套装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直斜面向下.自图示位置起,杆ab受到大小为F=0.5v+2(式中v为杆ab运动的速度,力F的单位为N)、方向平行导轨沿斜面向下的拉力作用,由静止开始运动,测得通过电阻R的电流随时间均匀增大.g取10m/s2. ①试判断金属杆ab在匀强磁场中做何种运动,并请写出推理过程; ②求电阻的阻值R; ③求金属杆ab自静止开始下滑通过位移x=1m所需的时间t和该过程中整个回路产生的焦耳热Q. 在t=0.5s内产生的焦耳热 “应用数学处理物理问题的能力”是物理学科高考考试说明中的五条能力要求之一.高考物理试题的解答离不开数学知识和方法的应用,以物理题为载体渗透考查数学能力是高考命题的永恒主题.在现行数学教材已经加入了微积分知识的情况下物理教育者不要回避这一问题,要能够做到与时俱进,在原有学科教学的基础上向前迈出小小的一步,以期学生对高中物理知识能够产生豁然开朗的感觉,因为只有教师做到真正的不回避学生才能做到真正的不惧怕.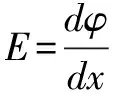

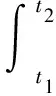

四、微积分知识教学感悟

