遗传算法优化灰色神经网络的GPS高程拟合模型

张 锦，赖祖龙

遗传算法优化灰色神经网络的GPS高程拟合模型

张 锦，赖祖龙

（中国地质大学 地理与信息工程学院，武汉 430074）

为了进一步提高GPS高程拟合的精度，提出利用遗传算法优化选择灰色神经网络模型的权值阈值：对灰色神经网络的初始权值和阈值利用遗传算法进行适应度编码，并经过选择、变异及交叉确定最优的初始参数，以解决灰色神经网络初始参数随机选择拟合值无法唯一确定的问题；然后建立遗传灰色神经网络GPS高程拟合模型，并给出模型实现步骤。实验结果表明，遗传灰色神经网络GPS高程拟合模型的精度优于当前其他拟合模型的精度，且模型稳定性良好。

全球定位系统高程拟合；遗传算法；灰色神经网络；参数优化；拟合精度

0 引言

全球定位系统（global positioning system, GPS）作为一种实时、高效的全球卫星定位技术，不但可以提供平面坐标还可以测量高程信息；但是GPS平面坐标的使用远远多于高程信息。而之所以GPS测量的高程使用无法像平面定位那么普及，是因为高程系统的原因。在我国国家规定正常高系统为统一的实际使用的高程系统，而GPS技术的高程是在大地高高程系统下测得的，所以不能直接使用GPS获得的高度数据[1]。正常高是以似大地水准面为基准，而大地高是以参考椭球面为起算基准，二者之间的差异叫做高程异常。要利用GPS 得到正常高需要进行高程拟合，方法之一是利用GPS/水准点测量得到的每个点的大地高和正常高数据，再计算得到每一个点的高程异常，之后使用相应的模型来拟合该测区的整体的高程异常，然后，只要知道一个点的GPS 3维数据就可以先使用平面数据求其高程异常值，再通过高程异常值和大地高确定该点的正常高[2-3]。目前，国内外普遍采用的GPS高程转换的方法主要有以下几种：①重力测量法[4]；②数学拟合法[5]；③平差转换法[6]；④联合平差法[7]；⑤神经网络法[8-9]。但是这些方法都有着各自的优缺点，如：重力测量法要获取大量重力测量数据，而且有涉密的可能，一般工程应用中可以使用此方法的情况较少；数学拟合法仅适合在地势平坦的小范围测区使用，无法满足在工程实际中的精度要求；灰色神经网络模型是由灰色模型和神经网络模型组合得到的新模型，其不但可以利用神经网络出色的自适应学习和非线性动态寻优能力有效地对灰色模型进行训练，而且只需要少量的实际测量数据便可以完成非线性拟合并得到精确的预测结果。

本文提出遗传算法优化灰色神经网络的GPS高程拟合模型。由于灰色神经网络模型的权值阈值并不是唯一确定的，这就导致每次预测结果完全不相同并可能产生较大的预测偏差，因此该模型的权值阈值的选择对于预测精度至关重要。本文采用遗传算法（genetic algorithm GA）的全局优化能力优化模型的权值和阈值，构建灰色神经网络GPS高程拟合模型，并利用拟合模型对GPS数据进行拟合。

1 遗传灰色神经网络GPS高程拟合模型

1.1 灰色神经网络GPS高程拟合模型

灰色模型能够通过少量的样本数据较好地预测样本的总体趋势。建立模型过程中为了减弱随机干扰的影响，序列往往采用累加生成，且生成的序列具有单调增加的规律。因此，可以通过在神经网络前对输入数据利用灰化层进行处理，其后利用白化层对输出数据进行还原，这样便可以将灰色系统与神经网络结合起来形成灰色神经网络预测模型，最终得到精确的计算结果。灰色神经网络拓扑结构如图1所示，其中：表示输入参数的序号；LA、LB、LC、LD分别表示灰色神经网络的4层。

图1 网络拓扑结构

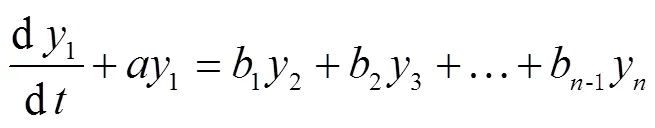
微分方程解的表达式为

式中

转化得到

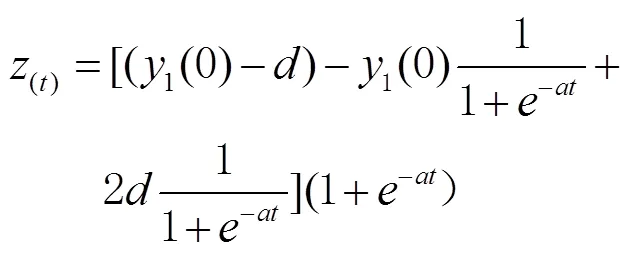
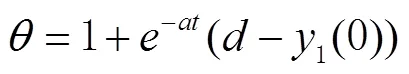
将GPS测得的点位平面坐标和对应点的高程异常作为训练样本构造灰色神经网络。以平面点位坐标为灰色神经网络的训练输入，高程异常数据作为训练输出，本次建立的灰色神经网络GPS高程拟合模型输入数据为2维，输出为1维，通过样本训练得到相应的灰色神经网络GPS高程拟合模型。

1.2 遗传算法优化的灰色神经网络模型

美国教授Holland于1962年首先提出遗传算法。遗传算法是一种借鉴生物界的适者生存、优胜劣汰以及遗传进化原理并用于随机化搜索最优值的方法[10]。它首先需要对个体进行遗传编码，并利用合适的适应度函数对所有的个体进行适应度计算。通过模拟自然界中物竞天择的自然法则，使不适者不断被淘汰，优秀的个体得到保留并通过选择、变异、交叉的遗传学原理使种群中的下一代持续进化，整个种群的适应度逐步提高。这样便可以通过不断的优化选择使整个种群朝预期方向进化。

由于灰色神经网络权值和阈值初始化时是随机的，所以可能造成灰色神经网络结果为局部收敛。利用遗传算法的参数优化能力，优化灰色神经网络的初始权值和阈值。通过遗传算法的个体编码将种群初始化，利用选择、变异、交叉等操作寻找最佳的灰色神经网络的初始参数，使初始参数唯一确定，从而提高灰色神经网络的预测结果的精度。具体实现步骤如下：

1）灰色神经网络初始化，并编码网络初始参数，设置遗传算法初始参数；

2）输入高程异常值通过灰色神经网络预测误差计算种群中每个个体的适应度；

3）对种群中适应度高的个体进行变异和交叉并繁衍下一代的个体，形成新的种群并计算种群中个体的最大适应度；

4）当种群达到进化代数或最大适应度不再变化时停止进化进入5），否则回到2）；

5）选取种群中适应度最大的个体并解码得到最佳的权值和阈值；

6）遗传算法得到最优权值阈值的灰色神经网络对输入的高程异常值进行训练，得到高程异常拟合值。

2 实验与结果分析

2.1 计算方案

本次实验数据为河南省某区域的GPS网数据并和水准进行联测得到。在实验区域中一共布设了43个GPS控制点并对这些点进行了水准的联测，点的精度均满足要求。在实验区域内的点位分布如图2所示。选取其中均匀分布的32个点作为训练样本，其余11个点为测试样本用于检测模型的拟合精度。采用4种不同拟合模型并计算各检测点的误差以及外符合精度。方案1为二次曲面拟合模型；方案2为灰色神经网络模型；方案3为BP神经网络模型；方案4为遗传算法优化的灰色神经网络模型。

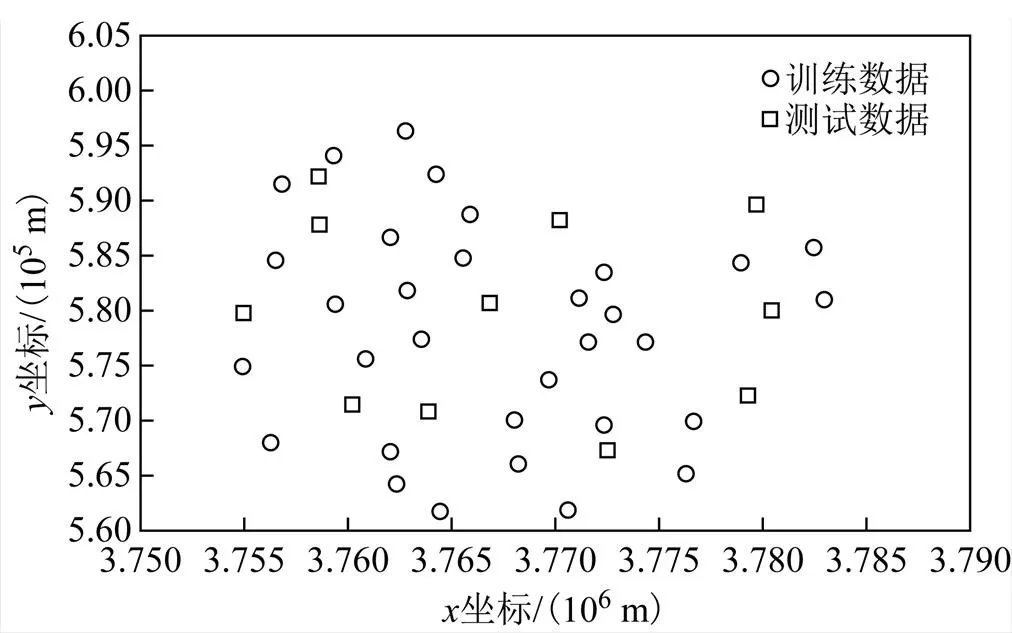
图2 测区点位分布

将43组数据归一化至[0,1]区间内，遗传算法初始参数设置：种群规模为120，遗传算法编码长度为21，使用随机遍历采样、单点交叉，交叉概率为0.8；编译概率为0.03；最大遗传代数为30。分别采用上述4种方案对32组训练样本数据进行建模，对11组数据进行预测，各个方案的计算结果以及预测误差如表1所示，各方案的误差曲线如图3所示。

表1 不同拟合方案结果对比

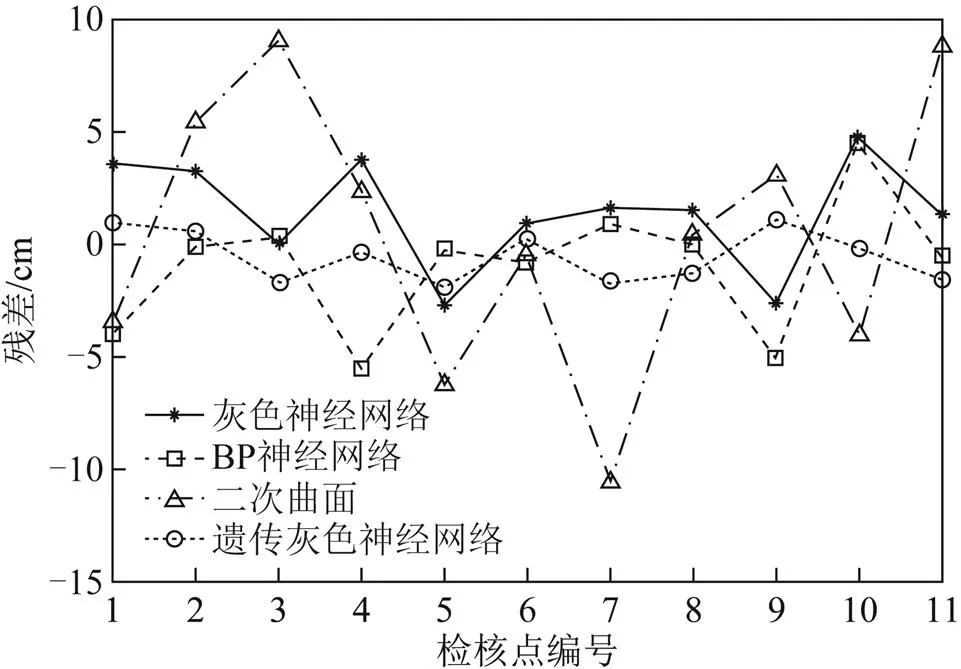
图3 残差对比

2.2 结果分析

从表1和图3可以发现：二次曲面拟合法的精度最差，平均误差4.89，外符合精度6.19,其中最大误差达到10.66 cm，并且二次曲面拟合的残差曲线波动幅度最大；BP神经网络的平均误差为2.01，外符合精度3.07，灰色神经网络的平均误差为2.36，外符合精度2.84 cm；本文提出的遗传灰色神经网络法的拟合精度最高，平均误差为1.05，外符合精度1.27，最大残差仅为1.92 cm，此外还可以发现其残差曲线的波动性最小，拟合时的稳定性最好。通过此次实验可以证明本文提出的模型具有较强的应用价值。

3 结束语

本文提出了利用遗传算法优化灰色神经网络的GPS高程拟合模型，并利用实际工程数据验证模型的精度和可靠性，与已有常见模型对比分析后得到以下结论：①就GPS高程拟合的精度而言，本文提出的GPS高程拟合模型精度高于二次曲面、BP神经网络、灰色神经网络；②由于遗传算法对于初始参数的优化使模型具有较好的稳定性；③本文的研究能够为实际工程项目提供一种行之有效的高程拟合方案，为GPS高程拟合的其他研究提供参考。

[1] 徐绍铨, 李振洪, 吴云孙. GPS高程拟合系统的研究[J]. 武汉大学学报(信息科学版), 1999, 24(4): 336-340.

[2] 徐绍铨, 张华海, 杨志强. 测量原理及应用[M]. 武汉: 武汉大学出版社, 2011.

[3] 宁津生, 刘经南, 陈俊勇, 等. 现代大地测量理论与技术[M]. 武汉: 武汉大学出版社, 2006.

[4] 田福娟. 顾及地球重力场模型的GPS水准高程拟合[J]. 地理空间信息, 2007, 5(4): 35-37.

[5] 于来法. 用数值拟合法确定GPS正常高的研究[J]. 测绘科学技术学报, 1996, 13(2): 90-94.

[6] 伍青云. GPS高程拟合的方式及可靠性分析[J]. 中国煤炭地质, 2006, 29(3): 29-31.

[7] 田建波, 曾志林. 利用GPS高求取正常高的几种拟合方法[J]. 海洋测绘, 2004, 24(2): 15-18.

[8] 刘常弘, 曾云, 杨帆. 基于Matlab的BP神经网络法GPS高程转换研究[J]. 工程地球物理学报, 2009, 6(4): 525-528.

[9] SONG L, HUANG T, FANG J, et al. Conversion of GPS height based on Bayesian regularization BP neural network[J]. Journal of Southwest Jiaotong University, 2008, 43(6): 724-728.

[10] 林勤. 基于遗传算法优化灰色神经网络的浙江省公路客运量预测模型[D]. 武汉: 华中师范大学, 2013.

GPS elevation fitting model of grey neural network optimized by genetic algorithm

ZHANG Jin, LAI Zulong

（College of Geography Information Engineering, China University of Geosciences, Wuhan 430074, China）

In order to further improve the accuracy of GPS elevation fitting, the paper proposed to use genetic algorithm to optimally select the weights and thresholds of grey neural network model: the initial weights and thresholds of grey neural network were encoded with fittness by genetic algorithm, and the optimal initial parameters were determined through selecting, mutating and crossing, for helping uniquely confirming the random selection fitting value of the initial parameters of grey neural network; then the GPS elevation fitting model was established with the genetic grey neural network, and the implementation steps of the model were given. Experimental result showed that the accuracy of the GPS elevation fitting model of the genetic grey neural network would be better than that of current other models, with a good stability.

elevation fitting of global positioning system; genetic algorithm; grey neural network; parameter optimization; fitting accuracy

P228

A

2095-4999(2019)03-0121-04

2018-12-21

国家自然基金项目（41504023）。

张锦（1995—），男，安徽合肥人，硕士生，研究方向为GNSS数据处理。

赖祖龙（1976—），男，江西于都人，博士，副教授，研究方向为变形监测理论与技术等。

张锦，赖祖龙.遗传算法优化灰色神经网络的GPS高程拟合模型[J].导航定位学报,2019,7(3):121-124.（ZHANG Jin, LAI Zulong.GPS elevation fitting model of grey neural network optimized by genetic algorithm[J].Journal of Navigation and Positioning,2019,7(3): 121-124.）

10.16547/j.cnki.10-1096.20190320.