一种适用于GNSS变形监测的滑动滤波模型

魏春晓，李博峰

一种适用于GNSS变形监测的滑动滤波模型

魏春晓，李博峰

（同济大学 测绘与地理信息学院，上海 200092）

针对GNSS变形监测数据处理中随机游走模型对局部时段快速变形带来的异常扰动抵抗能力较差，而常速度模型处理稳定变形的精度较低的问题，提出采用滑动滤波模型描述变形体的实际变形状态，并利用最小描述长度准则评估随机游走模型、常速度模型和滑动滤波模型在变形监测中的应用效果。结果表明，监测点稳定情况下滑动滤波模型平面精度可达到5 mm以内，且采用最小描述长度准则，能有效确定最优的滑动滤波模型，实现异常变形探测1 s内快速预警。

GNSS；变形监测；滑动滤波；最小描述长度；卡尔曼滤波

0 引言

变形监测作为一种先进的科学手段，能够有效预防某些自然灾害发生。应用全球卫星导航系统（global navigation satellite system，GNSS）构建自动化监测平台已成为变形监测领域发展的必然趋势[1-2]。目前变形监测数据分析方法主要有时间序列分析[3]、小波分析[4]、奇异谱分析[5]和神经网络[6]等，这些方法多着眼于事后处理。卡尔曼滤波在求解时不需要储存大量观测值，当得到新的观测数据时可立即更新滤波解，有效提高监测精度和稳定性，因此卡尔曼滤波在自动化变形监测领域得到了广泛应用[7-10]。

在变形监测应用中，由于监测体绝大部分时间比较稳定或者变化缓慢，因此卡尔曼滤波的运动学模型通常采用随机游走模型和常速度模型对变形状态进行简化[11]，但会引入一定的模型误差导致监测效果下降[12-13]。随机游走模型对局部时段快速变形带来的模型异常扰动抵抗能力较差，难以准确描述动态变化；常速度模型在处理稳定变形时滤波精度较低[14-15]。然而，滑动滤波模型能根据窗口长度调整状态转移矩阵及和状态噪声，从而能精确地描述变形体的实际变形状态，有望在变形监测中取得良好效果。本文采用稳定变形模拟数据和存在异常扰动变形模拟数据对随机游走模型、常速度模型和滑动滤波模型进行对比分析，并利用最小描述长度（minimum description length, MDL）准则定量评价存在异常扰动时3种模型的优劣。

1 卡尔曼滤波基本原理

卡尔曼滤波是一种在线性环境下，利用前1个历元的估计值和当前历元的观测值，以估计误差最小为准则不断递归，对动态系统状态进行最优估计的算法。

状态方程的本质是对系统附加历元间约束，系统的状态方程为

系统的观测方程为

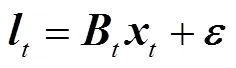
卡尔曼滤波包括两个基本步骤，即预报和更新，具体形式为

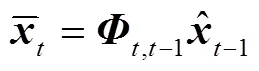
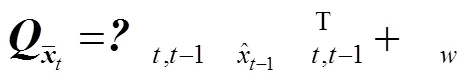
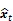
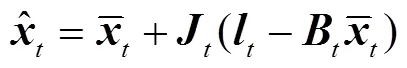
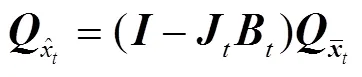
2 滤波运动学模型

2.1 随机游走模型

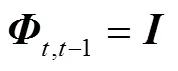
2.2 常速度模型

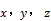
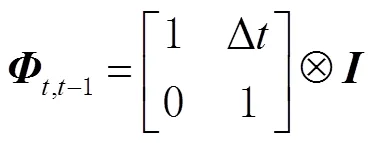
2.3 滑动滤波模型

采用随机游走模型滤波精度较高，但难以正确描述变形发生的时间和变形量的大小；常速度模型抵抗异常扰动能力较强，但在处理稳定变形时精度较低。在综合以上两种模型特点的基础上，本文研究滑动滤波模型在变形监测中的应用效果。通过设置不同长度的窗口，可以较为恰当地描述变形体的变形情况。为了提高初始化效率，通常在初始化阶段假设变形体稳定，采用随机游走模型。模糊度固定之后，对于每个窗口的第1个历元，将状态转移矩阵置为零矩阵，即不继承之前窗口的坐标和其协方差阵；将状态噪声置为无穷大，即只利用观测方程的信息进行解算，状态方程失效。对于每个窗口除第1个历元之外的其他历元，将状态转移矩阵置为单位阵，即继承之前窗口的坐标和其协方差阵；将状态噪声置为0，进行静态解算，等效于法方程累加。图1为滑动滤波模型的具体实现流程。

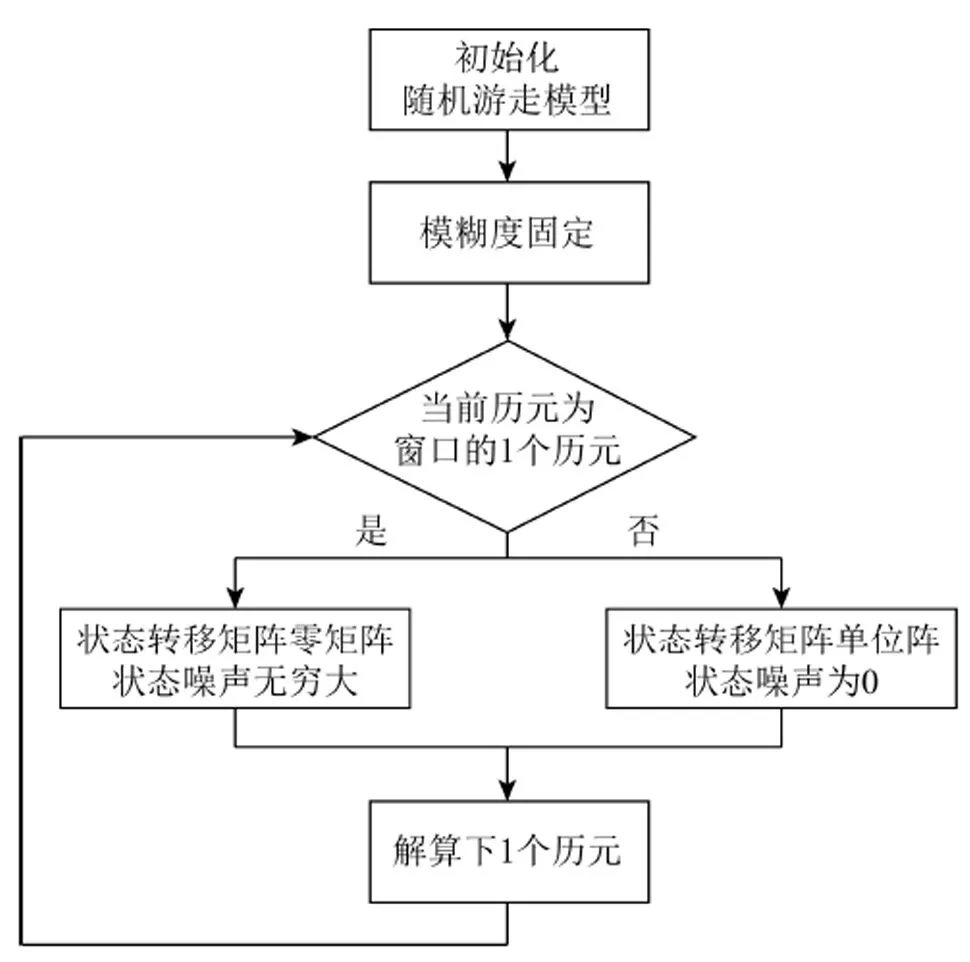
图1 滑动滤波模型实现流程

3 模型评价指标

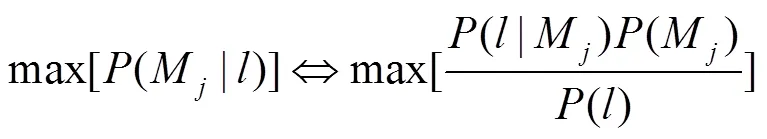
对式(10)两边进行负自然对数变换，得到等价形式为

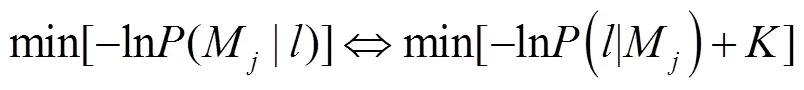
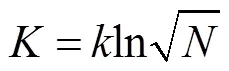
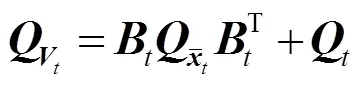
根据文献[18]提出的MDL原则，模型评价指标可表示为

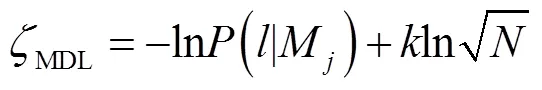
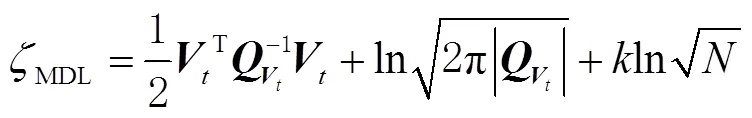
4 算例分析

4.1 稳定变形分析

为分析3种模型在稳定变形情况下的监测效果，采用2台固定放置于测绘学院楼顶、配置北斗卫星导航系统（BeiDou navigation satellite system, BDS）和全球定位系统（global navigation system, GPS）双模单频u-blox定位模块的GNSS接收机采集数据。观测日期为2017-10-15，观测时长约14 h，数据采样间隔1 s，卫星截止高度角10°，模糊度固定的ratio检验阈值设为2.5，观测频率为GPS的L1和BDS的B1波段，基线长约20 m。实验方案设计见表1。

表1 稳定分析方案设计

图2给出了采用4种方案得到的固定解在东（east，）、北（north，）、上（up，）3个坐标分量的序列。表2给出了4种方案求解结果在、、方向上的标准差（standard deviation，STD）和平均值（average，AVE）。从图2和表2中可以看出，对于稳定变形模拟数据而言，4个方案平面精度均在5 mm以内，高程精度在10 mm左右。在4种方案中，随机游走模型在方向上的坐标序列的STD最小，坐标序列变化最平稳，对变形状态的刻画精度最高。常速度模型求解时考虑了变形体的速度变化，平面方向上STD最大，滤波精度最差。滑动滤波模型采用不同窗口长度求得的坐标结果不同。随窗口长度增加，滑动滤波模型在方向上的坐标序列的STD逐渐减小，监测效果从常速度模型逐渐趋近于随机游走模型。4种方案在、、、方向上的坐标序列的AVE基本一致。

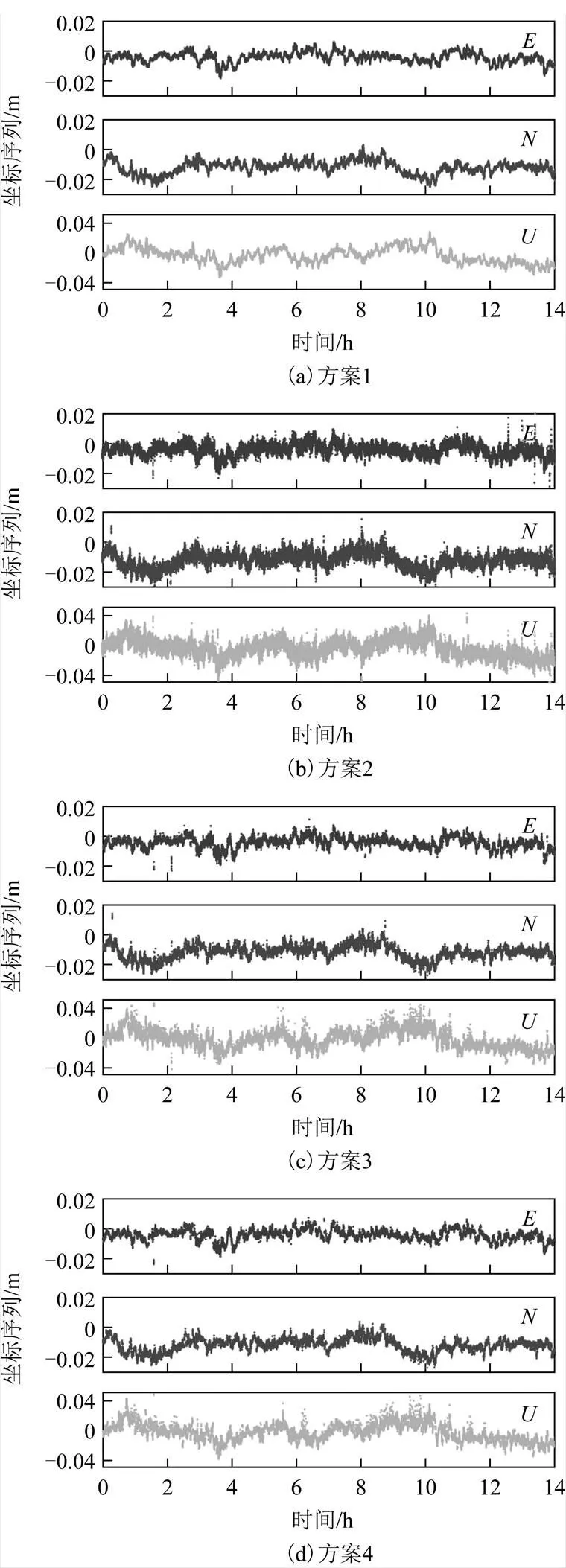
图2 4种方案固定解E、N、U方向坐标序列

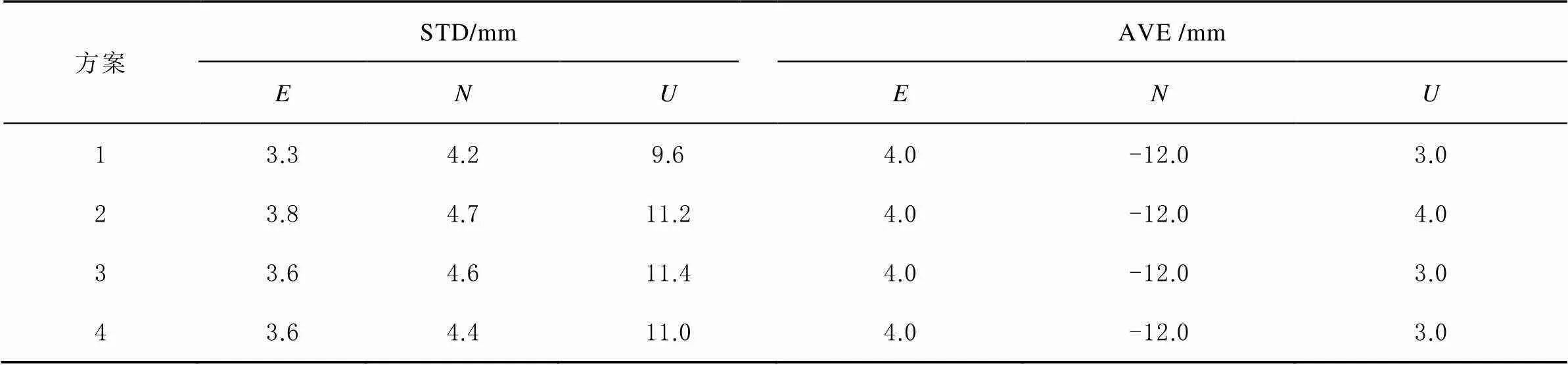
表2 4种方案定位结果统计

4.2 存在异常扰动变形分析

为分析3种模型对局部时段快速变形带来异常扰动的抵抗能力，设计如下实验：基准站固定，实验人员手持流动站先保持静止一段时间，然后在GPS秒为442248 s时将流动站迅速提升并移动一段距离，之后继续保持静止。观测日期为2018-05-11，观测时间约20 min，基线长约10 m，其余参数设置与稳定变形分析实验一致。具体方案设计见表3。

表3 存在异常扰动分析方案设计

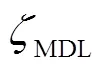
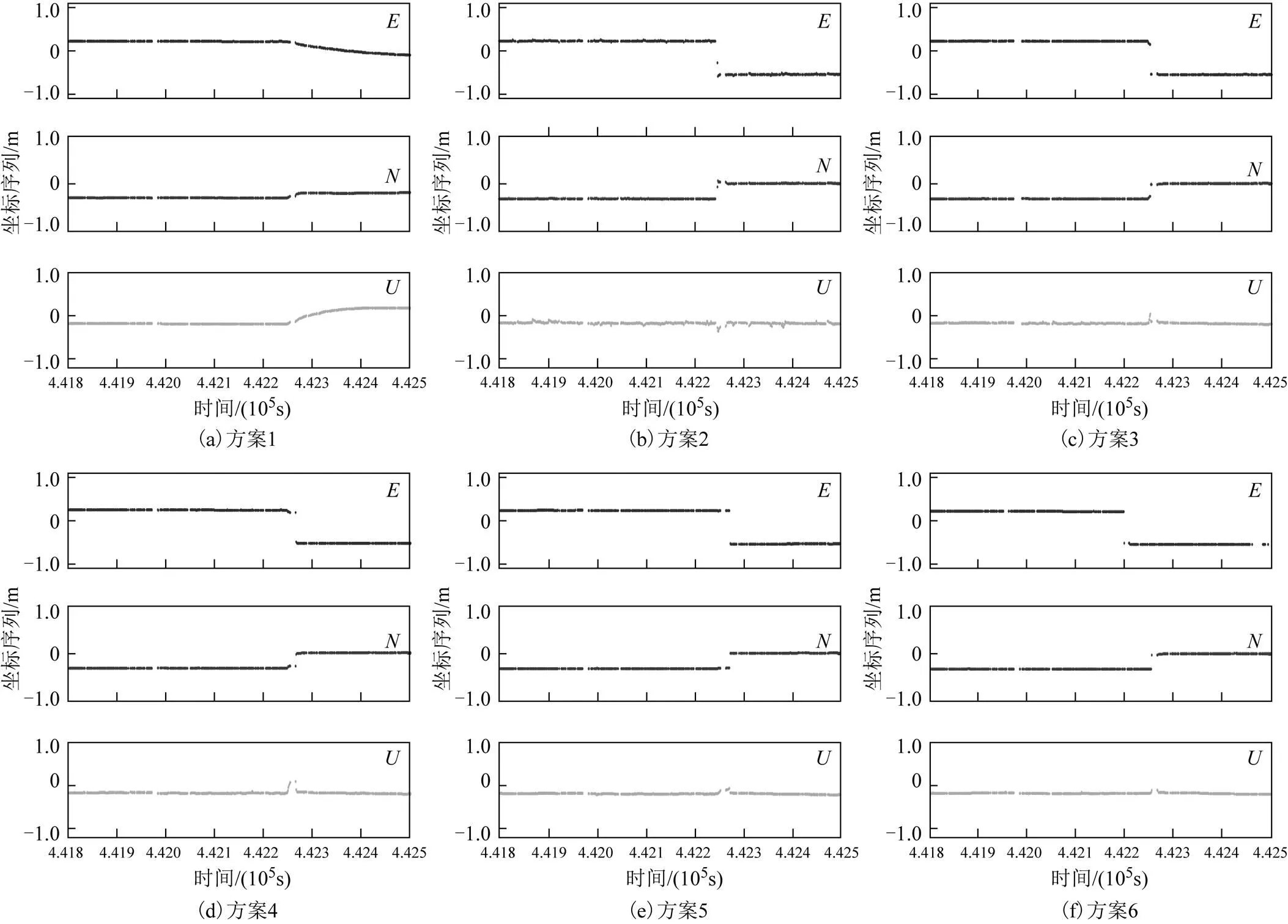
图3 6种方案固定解E、N、U方向坐标序列

表4 6种方案存在异常扰动变形分析

5 结束语

[1] 卫建东. 现代变形监测技术的发展现状与展望[J]. 测绘科学, 2007, 32(6): 10-13.

[2] 胡友健, 梁新美, 许成功. 论GPS变形监测技术的现状与发展趋势[J]. 测绘科学, 2006, 31(5): 155-157.

[3] 梅红, 岳东杰. 时间序列分析在变形监测数据处理中的应用[J]. 现代测绘, 2005, 28(6): 14-16.

[4] 章浙涛, 朱建军, 匡翠林, 等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报, 2014, 43(1): 13-20.

[5] 李世友, 王奉伟, 沈云中. 大坝变形时间序列的奇异谱分析[J]. 测绘通报, 2018(9): 64-68.

[6] 王穗辉, 潘国荣. 人工神经网络在隧道地表变形预测中的应用[J]. 同济大学学报(自然科学版), 2001, 29(10): 1147-1151.

[7] 王利, 李亚红, 刘万林. 卡尔曼滤波在大坝动态变形监测数据处理中的应用[J]. 西安科技大学学报, 2006, 26(3): 353-357.

[8] 徐亚明, 刘冠兰, 柏文锋. 顾及基坑施工影响的地铁区间隧道结构卡尔曼滤波预报模型[J]. 武汉大学学报(信息科学版), 2013, 38(11): 1322-1325.

[9] 高井祥, 郑南山, 余学祥. GPS技术在矿区井筒变形监测中的应用[J]. 全球定位系统, 2001, 26(4): 45-49.

[10] INCE C, SAHIN M. Real-time deformation monitoring with GPS and Kalman filter[J]. Earth Planets and Space, 2000, 52(10): 837-840.

[11] 刘大杰, 于正林. 动态测量系统与卡尔曼滤波[J]. 测绘学报, 1988, 17(4): 254-262.

[12] 陶本藻. 卡尔曼滤波模型误差的识别[J]. 地壳形变与地震, 1999, 19(4): 15-20.

[13] 许阿裴, 归庆明, 韩松辉. 卡尔曼滤波模型误差的影响分析[J]. 大地测量与地球动力学, 2008, 28(1): 101-104.

[14] 戴吾蛟, 伍锡锈. 变形监测中Kalman滤波状态模型的比较分析[J]. 大地测量与地球动力学, 2009, 29(6): 88-92.

[15] 伍锡锈. 动态变形监测中的Kalman滤波方法研究[D]. 长沙: 中南大学, 2011.

[16] ZHOU Z B, LI B F. GNSS windowing navigation with adaptively constructed dynamic model[J]. GPS Solutions, 2015, 19(1): 37-48.

[17] LI L, KUHLMANN H. Deformation detection in the GPS real-time series by the multiple Kalman filters model[J]. Journal of Surveying Engineering, 2010, 136(4): 157-164.

[18] RISSANEN J. A universal prior for integers and estimation by minimum description length[J]. Annals of Statistics, 1983, 11(2): 416-431.

Moving filtering model for GNSS deformation monitoring

WEI Chunxiao, LI Bofeng

（College of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China）

In order to solve the problem that the random walk model has poor resistance to abnormal disturbance caused by rapid local deformation, while the constant velocity model has low accuracy in dealing with stable deformation, the moving filtering model is used to describe the actual deformation state of the deformation body. The minimum description length criterion is used to evaluate the random walk model, the constant velocity model and the moving filtering model in deformation monitoring. The results show that the plane accuracy of the moving filtering model can be less than 5 mm under the condition of stable deformation, and the optimal moving filtering model can be effectively determined by using the minimum description length criterion, to realize the rapid early warning of abnormal deformation detection within 1 s.

GNSS；deformation monitoring；moving filtering；minimum description length；Kalman filtering

P228

A

2095-4999(2019)03-0125-06

2018-12-28

国家自然科学基金项目（41874030，41622401，41574031）；上海市科技委员会科技创新行动计划项目（17511109501）。

魏春晓（1995—），女，山东枣庄人，硕士生，研究方向为GNSS变形监测理论与应用。

李博峰（1983—），男，陕西咸阳人，博士，教授，研究方向为卫星精密定位与导航位置服务的理论与应用技术。

魏春晓，李博峰.一种适用于GNSS变形监测的滑动滤波模型[J].导航定位学报,2019,7(3):125-130.（WEI Chunxiao,LI Bofeng.Moving filtering model for GNSS deformation monitoring[J].Journal of Navigation and Positioning,2019,7(3):125-130.）

10.16547/j.cnki.10-1096.20190321.