水下传感网络的三维定位算法

吕品品

水下传感网络的三维定位算法

吕品品

（淄博职业学院 信息工程系，山东 淄博 255000）

为了进一步提高水下传感网络的节点定位精度，提出基于声信号测距的定位算法（ASRL）：将锚节点部署于水表面, 且锚节点周期性地传输beacon包；在声信号测距的定位算法中，普通节点先通过声信号的球形传播模型测距，然后再利用获取的测距信息结合欧几里德几何学估计自己的位置；最后通过实验评估ASRL算法的定位性能。仿真结果表明，与LSL算法相比，ASRL定位算法具有较低的定位误差和较高的定位覆盖率。

水下传感网络；测距；球形传播模型；欧几里德几何学；定位覆盖率

0 引言

随着陆地无线传感网络（wireless sensor networks, WSNs）研究的迅速发展，水下传感网络（underwater sensor networks, USNs）已成无线网络的研究热点[1-2]。USNs在海洋资源探测和海洋信息获取等方面的重要应用得到各国的广泛关注。

然而，在实际实用中，由于无线电波在水中衰减迅速，通过无线链接水下传感节点存在巨大的挑战。为此，USNs常采用水声通信[3]，如图1所示。水下传感节点通过声通信传输信息，而位于水面的信宿收集信息后，利用无线电信号将信息传输至控制中心。

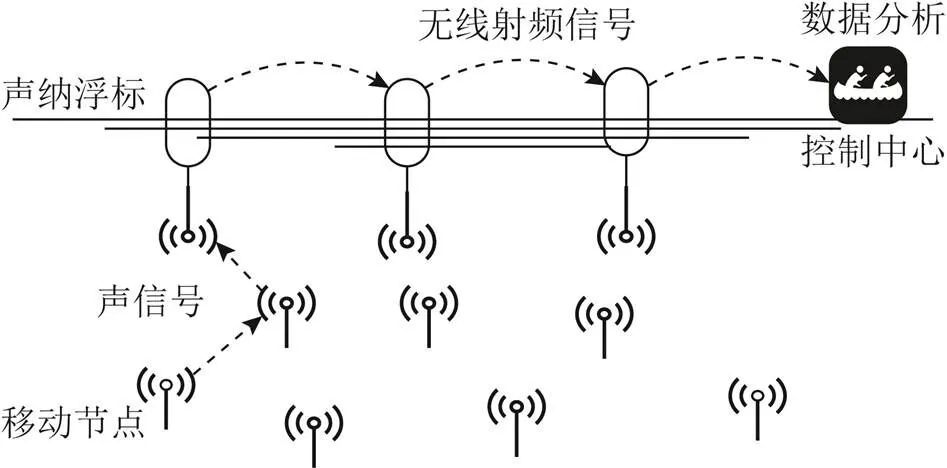
图1 USNs示意

此外，定位也是USNs的重要技术，即在给定水域部署一些传感节点，如何通过一些参考节点寻找传感节点的空间位置[4]。估计节点位置是许多网络操作环境的最重要的性能要求，如路由协议、事件检测以及网络维护。此外，水下定位比陆地定位更具有挑战性，原因在于水域信号传播的复杂性[5]。

目前研究人员已针对UWNs中节点定位提出了不同的定位算法[6]。现存的定位算法可分为测距定位和非测距定位2类。在测距定位算法中，先通过获取信号的信息，如到达时间、角度、估计距离，然后再依据距离计算节点的位置。而非测距定位算法是指通过传输跳数或区域特性估计节点位置。这2类算法特性不同，测距定位算法的精度高于非测距定位算法，但是，测距定位算法需要添加额外的设备测量距离。

在多数现存的具有代表性的测距定位算法[7]中，均需要已知位置的参考节点。未知节点通过测量与参考节点间的距离来估计自己位置。

多点定位是另一类定位算法。多点定位允许节点先估计自己位置，然后在给定的约束条件下最小化定位误差，进而修正定位位置。除了常见的基于球的最小二乘算法外，还有混合定位算法[8]。

文献[9]提出了新的定位方案。先部署特殊的“流浪者”节点，它们依据水域的实时情况调整深度。这些“流浪者”随水移动，并收集链路信息，最后估计节点位置。文献[10]也提出了基于潜水节点beacon包的定位算法（dive node rise, DNR），DNR通过浮标周期地广播beacon包。接收节点依据估计与浮标距离进行定位。

此外，文献[11]通过周期广播的beacon包测量到达时间（time of arrival, TOA）进行测距。文献[12]利用水面上的全球定位系统（global position system, GPS）浮标，提出最小二乘格型（least squares lattice, LSL）的定位方案，且这些浮标位置已知。再利用这些浮标和锚节点位置，估计节点位置，一旦获取节点位置，又将这些节点作为锚节点，逐步扩大锚节点位置，进而扩大节点位置。

为此，针对水下传感网络，提出基于声信号测距的定位算法（acoustic signal-ranging based localization, ASRL）。ASRL算法利用锚节点所发出的beacon包，并通过球形传播模型，估计节点与锚节点间距离。然后再利用欧几里德几何学，估计节点位置。实验数据表明，提出的ASRL算法能够有效地降低定位误差。

1 ASRL算法

提出的ASRL定位算法采用锚节点和测距定位技术。先在系统中部署一些已知位置的节点，将这些节点称为锚节点。而其他未知位置的节点称为普通节点，普通节点通过锚节点估计自己的位置。

然而，并非所有节点均在锚节点的通信范围内。因此，当普通节点估计了自己位置后，也称为新的锚节点，并广播自己位置，直到网络内所有节点均获取了自己的位置。

1.1 测距模型

ASRL定位算法是基本测距的定位算法。因此，首先建立水声信道传播损耗模型，然后再依据所接收的声强度估计离声源的距离，即测距。

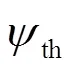
传输损耗TL，可理解为：声源所发出的声强度以声压力波向外传递时所产生衰减值。假定从声源发生处与接收端相距米，则TL的定义为

SL表示辐射信号强度，单位为dB，其计算式为

由于ASRL算法引用球形传播模型，在水声信道中信号传输米发生的损耗为

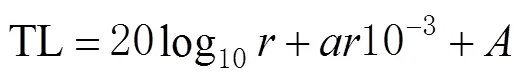
式中：为水下信道的异常传输损耗；为水对声信号的吸收系数。

1.2 位置估计

图2 3个锚节点的定位模型

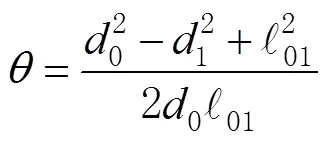
利用2个锚节点只能将节点位置局限于一个平面圆上。因此，为了进一步明确普通节点的位置，需要再利用第3个锚节点2信息。为此，定义3个正交单位矢量为

普通节点位于圆的周长上，其位置可以表示为

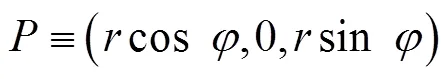
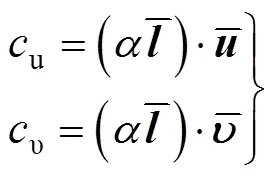
如图3所示，节点P的2个可能位置分别位于圆的对称点上。若节点P能够进一步获取离第4个锚节点的距离信息，则可确定节点P的位置。反之，若不能获取与第4个锚节点的距离信息，则将这2个位置的任意一个位置作为节点P的位置估计值。

2 性能分析

2.1 实验环境

为了更好地分析ASRL定位算法的性能，选择LSL算法作为参照，并比较开销、定位覆盖率和定位误差性能。所谓开销是指每定位一个节点所需的控制消息条数；定位覆盖率是指能定位的节点数与总的节点数的比值；定位误差是指定位精度，其定义为

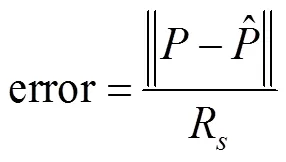
2.2 数据分析

2.2.1 实验一

1）定位覆盖率。定位覆盖率随节点密度变化的实验数据如图4所示。与LSL算法相比，提出的ASRL算法的定位覆盖率得到大幅度提升。这主要是因为ASRL算法只要3个锚节点便可估计节点位置，减少了对锚节点数量要求。

图4 定位覆盖率

图5 定位误差

2.2.2 实验二

图6 锚节点传输半径对定位覆盖率和定位误差的影响

3 结束语

针对水下传感网络的节点定位问题，提出基于声信号测距的水下传感网络定位ASRL算法。ASRL算法是基于锚节点和测距的定位算法。锚节点先周期性地广播包含自己位置信息的beacon包，普通节点接收后，利用球形传播模型估计离锚节点的距离，然后再结合欧几里德几何学估计节点的位置。仿真数据表明，提出的ASRL算法扩大了可定位的节点数，并减少了定位误差。

目前，本文只通过仿真分析了ASRL算法的定位性能，后期将其应用于真实水下环境应用中，如水中漂浮物体检测，ASRL算法在真实环境的性能等。

[1] AKTUKSUZ I F, POMPILI D, MELODIA T. Underwater acoustic sensor networks: research challenges[J]. Ad hoc Networks, 2015, 3(3): 257-279.

[2] AKTUKSUZ I F. Wireless sensor networks in challenged environments such as underwater and underground[C]// Association for Computing Machinery(ACM). Proceedings of the 17th ACM international conference on modeling, analysis and simulation of wireless and mobile systems. Montreal：ACM, 2014: 1-12.

[3] 高玲, 郑兴旺, 陈彭, 等. 一种水下无线传感网络中节能跨层路由协议[J]. 集美大学学报(自然科学版), 2014, 19(3): 230-236.

[4] 柳凡, 杜秀娟, 冯振兴, 等. 基于平均跳距的水下传感网络节点定位算法[J]. 计算系统应用, 2014, 23(4): 138-144.

[5] TAN H P, DIAMANT R D, SEAH W K. A survey of techniques and challenges in underwater localization[J]. Ocean Engineering, 2011, 38(14): 1663–1676.

[6] HAN G, JIANG J, SHU L. Localization algorithms of underwater wireless sensor networks: a survey[J]. Sensors, 2012, 12(2): 2026-2061.

[7] 王怿, 田臣, 黄本雄. 锚节点水面部署的三维水下传感网定位算法[J]. 微电子学与计算机, 2010, 27(10): 65-69.

[8] BIAN T, VENKATERAN R, LI C. An improved localization method using error probability distribution for underwater sensor networks[C]//The Institute of Electrical and Electronic Engineers(IEEE). Proceedings of the 2010 IEEE International Conference on Communications. Cape Town：IEEE, 2010: 1–6.

[9] MIRZA D, SCHURGERS C. Energy-efficient localization in networks of underwater drifters[J]. Selected Areas in Communications, 2012, 5(7): 23-31.

[10] EROL M, VIERIRA L F, GERLA M. Localization with dive’n’rise (dnr) beacons for underwater acoustic sensor networks[J]. IEEE Transactions on Mobile Computing, 2013, 6(9): 97-100.

[11] AMEER P, JACOB L. Localization using ray tracing for underwater acoustic sensor networks[J]. IEEE Communications Letters, 2010, 14(10): 930-932.

[12] ZHOU Zu, CUI Jiuhui. Efficient localization for large-scale underwater sensor networks[J]. Ad Hoc Networks, 2010, 8(3): 267-279.

[13] STOJANOVIC M. On the relationship between capacity and distance in an underwater acoustic communication channel[EB/OL].[2018-10-19].http://www.mit.edu/~millitsa/resources/pdfs/bwdx.pdf.

3D localization algorithm for underwater wireless sensor networks

LYU Pinpin

（Department of Information Engineering, Zibo Vocational Institute, Zibo, Shandong 255000, China）

In order to further improve the accuracy of node positioning for underwater sensor acoustic networks, the paper proposed the acoustic signal-ranging based localization algorithm (ASRL): the anchor nodes were deployed at the ocean surface with periodically broadcasting the beacon package; the distances were measured through a spherical propagation model of acoustic signals by ordinary nodes, and the location was estimated by using the measured 3D positions integrated with Euclidean geometrics; finally the positioning performance of ASRL algorithm was evaluated by simulation. Result showed that, compared with LSL algorithm, ASRL algorithm chould have lower positioning errors and a higher localization coverage rate.

underwater sensor acoustic networks; ranging; spherical propagation model; Euclidean geometrics; localization coverage rate

TPT393

A

2095-4999(2019)03-0011-06

2018-12-10

山东省淄博市2018年度重点研发计划项目（2018kj010132）。

吕品品（1981—），女，山东淄博人，硕士，讲师，研究方向为计算机网络、神经网络、云计算、网络空间安全等。

吕品品.水下传感网络的三维定位算法[J].导航定位学报, 2019,7(3):11-16.（LYU Pinpin.3D localization algorithm for underwater wireless sensor networks[J].Journal of Navigation and Positioning,2019,7(3):11-16.）

10.16547/j.cnki.10-1096.20190303.