联合使用多星座信号实时估计对流层延迟

许锡文，张志伟，李辰风

联合使用多星座信号实时估计对流层延迟

许锡文1，张志伟1，李辰风2

（1. 江西应用技术职业学院 测绘地理信息学院，江西 赣州 341000；2. 武汉大学 测绘学院，武汉 430079）

针对后处理或者近实时对流程延迟无法应用于时延要求严格的气象学，以及GPS单系统PPP所获取的ZTD性能相对较差等问题，提出1种GPS/GLONASS/Galileo/BDS 4系统组合PPP实时估计ZTD方法。研究结果表明：当截止高度角设为7°时，GPS单系统、GPS/GLONASS双系统、4系统组合PPP实时ZTD估值的收敛时间分别为11.4、10.5、9.8 min，估计精度分别为5.8、5.9、6.0 mm；当截止高度角设为40°时，3种不同星座组合情形中相应ZTD估值的可用性分别为56.4 %、91.1 %、98.2 %，估计精度分别为14.4、12.7、11.0 mm。

对流层延迟；精密单点定位；收敛时间；估计精度；可用性

0 引言

在水循环和气候变化中，大气水汽起到了很重要的作用。水汽辐射计和无线电探空仪等气象传感器最早被用于测量大气水汽，但这些传统的测量技术具有很多缺点，比如时空分辨率较低和成本较高。文献[1]在1992年首次提出全球定位系统（global positioning system, GPS）气象学概念，即使用地基接收机来测量水汽。GPS气象学具有全天候运行能力、低运营成本、广阔空间覆盖和高时间分辨率等优点。和来自于气象传感器的水汽估值相比，基于GPS的水汽估值精度相当[2]。精密相对定位技术和精密单点定位（precise point positioning, PPP）技术均可以用于GPS气象学研究，但后者在观测值需求和计算效率方面更具有优势，并且能够获得绝对的对流层天顶总延迟（zenith total delay, ZTD），而不是2个测站间的ZTD差值。

尽管业界在GPS气象学研究方面已经取得很大进展，但这些研究大多局限于后处理模式或者近实时模式[3-7]。大气水汽的时空变化很快。对于一些应用，比如极端天气即时预报，需要实时更新大气状态信息。使用PPP技术来实时估计ZTD或者大气可降水量（precipitable water vapor, PWV）需要应用实时精密卫星轨道和钟差改正值。国际全球卫星导航系统（global navigation satellite system, GNSS）服务（International GNSS Service, IGS）实时试验项目（real-time pilot project, RTPP）致力于实时精密卫星轨道和钟差产品的生成和播发。得益于近年来IGS RTPP的发展，这些产品目前可用于科学研究，这为使用PPP技术实时估计ZTD研究提供了基础。

近年来，卫星导航系统迅速发展，GNSS已经从单一的GPS扩展到GPS、格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）、伽利略卫星导航系统（Galileo navigation satellite system, Galileo）和北斗卫星导航系统（BeiDou navigation satellite system, BDS）4个系统共存。当4个GNSS星座全部部署完成时，将会有120颗以上GNSS卫星可用。PPP是1种基于卫星的技术，其性能在很大程度上由所观测到的卫星决定[8]。由于多系统组合可以增加可见卫星数、改善卫星的几何结构，因而可以预期提高PPP ZTD估值的可用性、可靠性、稳定性和精度。

本文提出1种GPS/GLONASS/Galileo/BDS 4系统组合PPP实时估计对流层延迟方法。目前，BDS正处于全球部署阶段，虽然其空间段中包含许多新一代BDS卫星，但仍缺乏这些卫星的精密改正产品，导致BDS服务区外许多区域的BDS可用卫星数很少。因此，本文选择位于亚太地区的26个测站进行分析，利用4系统组合PPP技术实时估计ZTD，从收敛时间、估计精度和可用性3个方面对实时ZTD估值性能进行了评估，并且与GPS单系统以及GPS/GLONASS双系统结果进行对比。

1 4系统组合PPP实时估计ZTD

使用消电离层（ionospheric-free, IF）组合来消除1阶电离层延迟的影响。在应用实时精密卫星轨道和钟差改正值，并且固定接收机坐标后，4系统组合PPP观测模型可以表示为

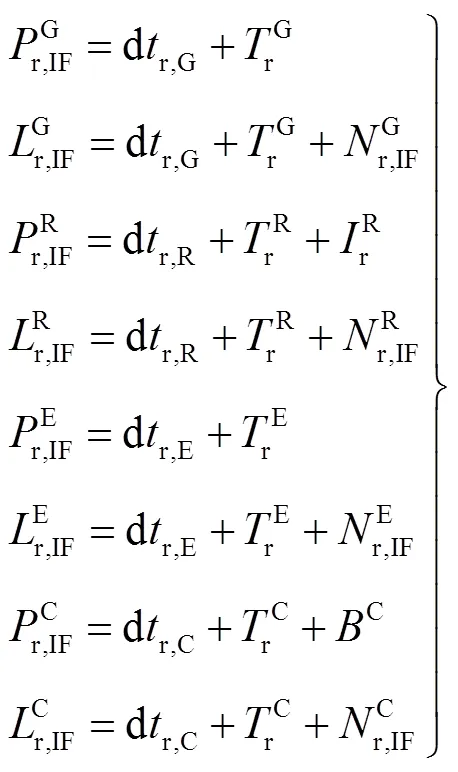
式中：r表示1个GNSS接收机；G、R、E、C分别表示GPS、GLONASS、Galileo、BDS卫星；和分别表示“观测的减去计算的”伪距和载波相位测量值；dr表示接收机钟差；表示斜路径对流层延迟；表示相位模糊度；表示频率间偏差（inter-frequency bias, IFB）；表示卫星诱发的伪距偏差（satellite-induced code bias, SICB）。式（1）中忽略了未模型化的测量噪声和多路径误差。由于吸收了接收机端、卫星端伪距硬件延迟和相位硬件延迟的影响，相位模糊度失去了整数特性。

BDS伪距观测值中存在1种特殊的SICB，而其他3个卫星系统均不存在这一问题。可以将SICB作为高度角的函数进行高精度建模，使用文献[9]中提出的SICB改正模型对各BDS卫星各频率上的伪距观测值进行改正。接收机端伪距硬件延迟和接收机钟差具有很强的相关性，因而在PPP中二者通常当做1个参数进行估计。不同的卫星系统一般采用不同的信号结构和频率，导致接收机端伪距硬件延迟对于4个卫星系统影响不同。为了解决这一问题，每个卫星系统均需要估计1个接收机钟差参数，因而式（1）中的4个接收机钟差参数是不同的。此外，GLONASS采用频分多址技术，当频率因子不同时，卫星的频率也会稍有差异，因而需要引入额外的IFB参数来补偿接收机端伪距硬件延迟的不同影响。原理上，频率因子相同的GLONASS卫星可以采用1个IFB参数；但文献[10]证明了即使频率因子相同时，不同卫星接收机端伪距硬件延迟也会有所不同：因而在本文中每颗GLONASS卫星均估计了1个IFB参数。为了消除接收机钟差参数dr,R和IFB参数间的秩亏，引入约束

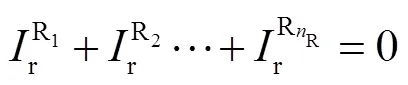
斜路径对流层延迟可以模拟为干分量、湿分量和对流层水平梯度的和，计算公式为

式中：S表示1颗GNSS卫星（G、R、E或者C）；h、w和g分别表示干映射函数、湿映射函数和梯度的映射函数；h和w分别表示天顶干延迟（zenith hydrostatic delay, ZHD）和天顶湿延迟（zenith wet delay, ZWD）；表示卫星方位角；N和E分别表示南北方向和东西方向的对流层水平梯度。

ZHD可以使用先验模型进行改正，而ZWD和2个梯度分量通常作为未知参数在PPP处理中进行估计。

式中表示估值向量。

ZTD包含ZHD和ZWD 2部分。根据先验模型计算得到的ZHD以及估计得到的ZWD，即

式中：t表示重建的ZTD；表示对流层延迟残差。可以使用t来评估4系统组合PPP实时测量大气参数的性能。

2 实验与结果分析

选择位于亚太地区的26个多GNSS试验（multi-GNSS experiment, MGEX）测站2017年4月6日的数据进行分析，图1给出了这些测站的地理分布。所有选择的测站均能够跟踪GPS、GLONASS、Galileo和BDS信号。表1给出了4系统组合PPP实时估计ZTD处理策略。

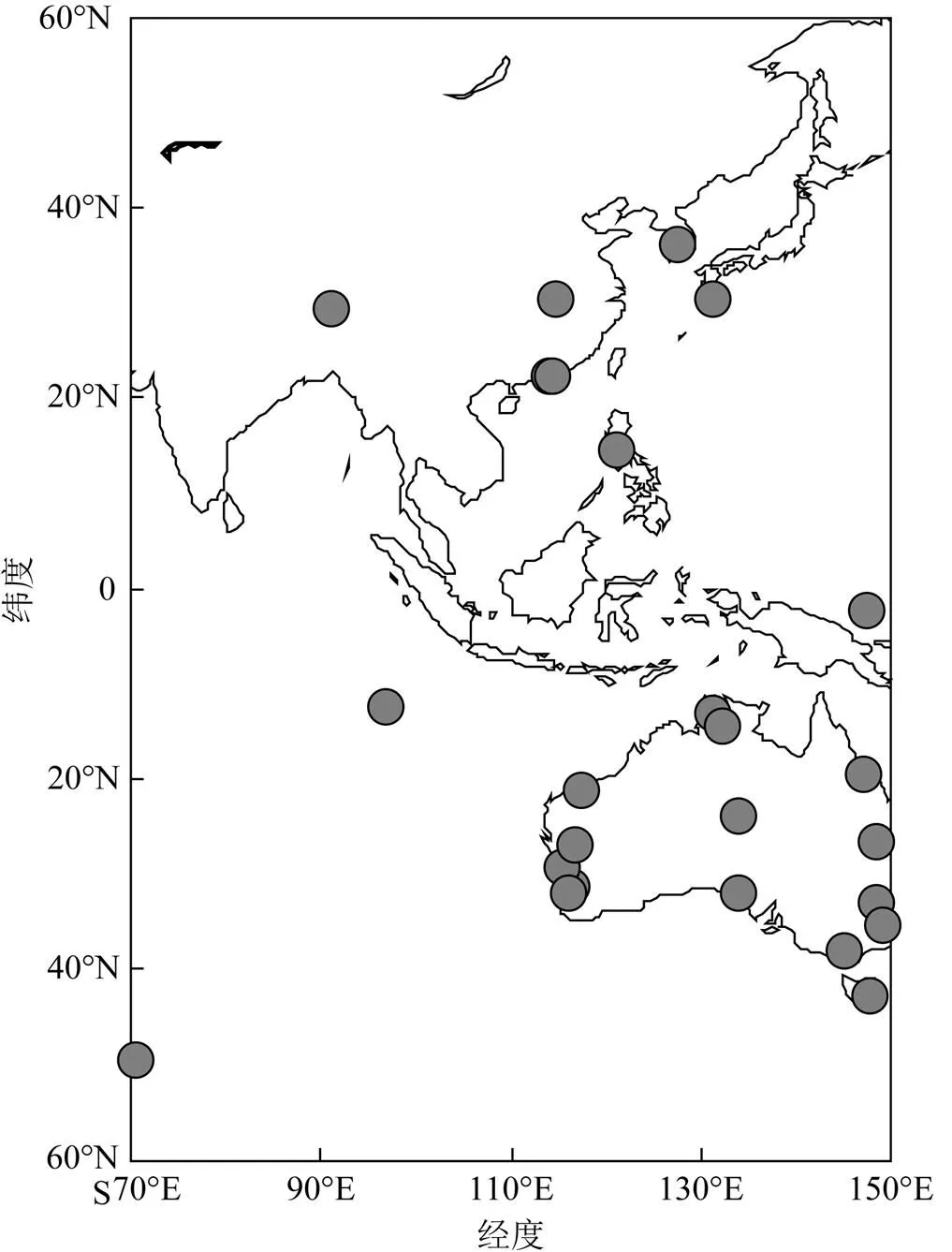
图1 26个MGEX站地理分布

表1 4系统组合PPP实时估计ZTD处理策略

目前，有多个分析中心可以提供实时精密卫星轨道和钟差产品，但大多数分析中心只提供GPS单系统或者GPS/GLONASS双系统实时精密产品。法国国家太空研究中心（Centre National d’Études Spatiales, CNES）提供的实时精密产品可以支持全部4个卫星系统，因而选用CNES产品进行分析。PPP ZTD估值的精度和可靠性受采用的实时精密产品性能影响很大，这里将德国地学研究中心（GeoForschungsZentrum, GFZ）最终产品作为参考评估了CNES实时精密卫星轨道和钟差产品的质量。表2提供了卫星轨道3维误差和钟差误差1 d内（2017-04-06）的均方根（root mean square, RMS）统计值。

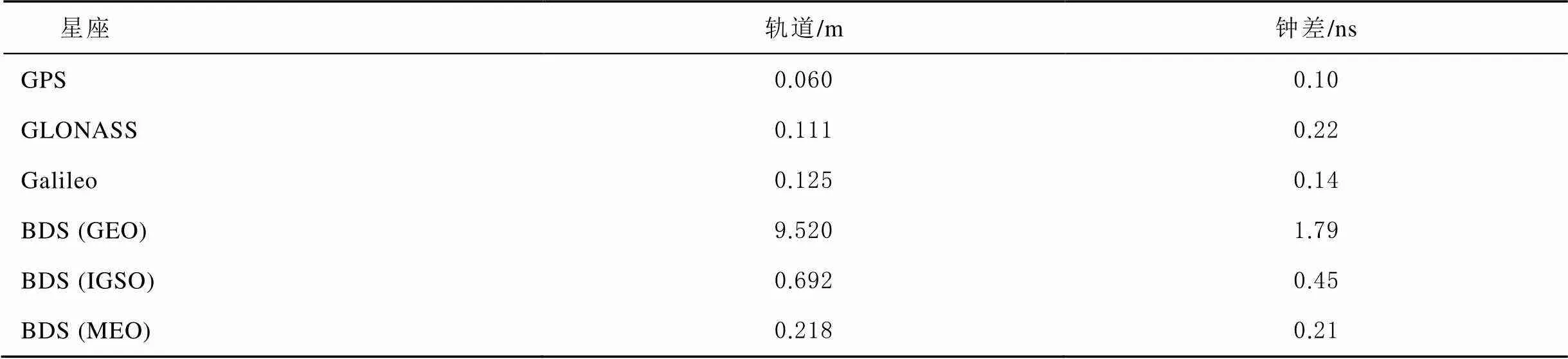
表2 CNES实时精密产品卫星轨道和钟差误差的RMS值

从表2中可知，GPS卫星轨道和钟差误差RMS值分别为0.060 m和0.10 ns，而GLONASS、Galileo和BDS 中圆地球轨道(medium Earth orbit, MEO)卫星相应的RMS统计值扩大了2~3倍。BDS倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)和地球静止轨道(geostationary Earth orbit，GEO)卫星轨道误差分别增加到0.692和9.520 m，而相应的钟差精度分别下降到0.45、1.79 ns。

根据CNES实时精密产品的质量分析，确定了观测值的随机模型。GPS卫星伪距和载波相位观测值的精度分别设定为0.3、0.003 m，GLONASS、Galileo和BDS MEO卫星相应的精度分别设定为0.6、0.006 m，而BDS IGSO卫星相应的精度分别设定为1.5、0.015 m。由于BDS GEO卫星轨道和钟差改正值精度太差，因而在解算中剔除了这些卫星。

图2给出了所有26个测站实时ZTD估值的收敛时间。在图2中，缩写GLO和GAL分别表示GLONASS和Galileo。在本文中，当有连续10个历元的ZTD误差小于20 mm时，认为ZTD估值已经收敛。收敛时间指的是从第1个历元到收敛历元之间的时间跨度。选择美国海军天文台（United States Naval Observatory, USNO）提供的最终对流层ZTD产品作为参考，计算了实时ZTD估值的误差。为了进行对比分析，选择了3种不同的星座组合，包括GPS单系统、GPS/GLONASS双系统和4系统。从图2可知，在大多数情况下，随着越来越多卫星系统的观测值参与解算，实时ZTD估值收敛时间逐渐缩短。表3给出了26个测站实时ZTD估值收敛时间的统计值，包括平均值和标准差（standard deviation, STD）。根据平均值可知，3种不同星座组合PPP实时ZTD估值的收敛时间分别为11.4、10.5、9.8 min。

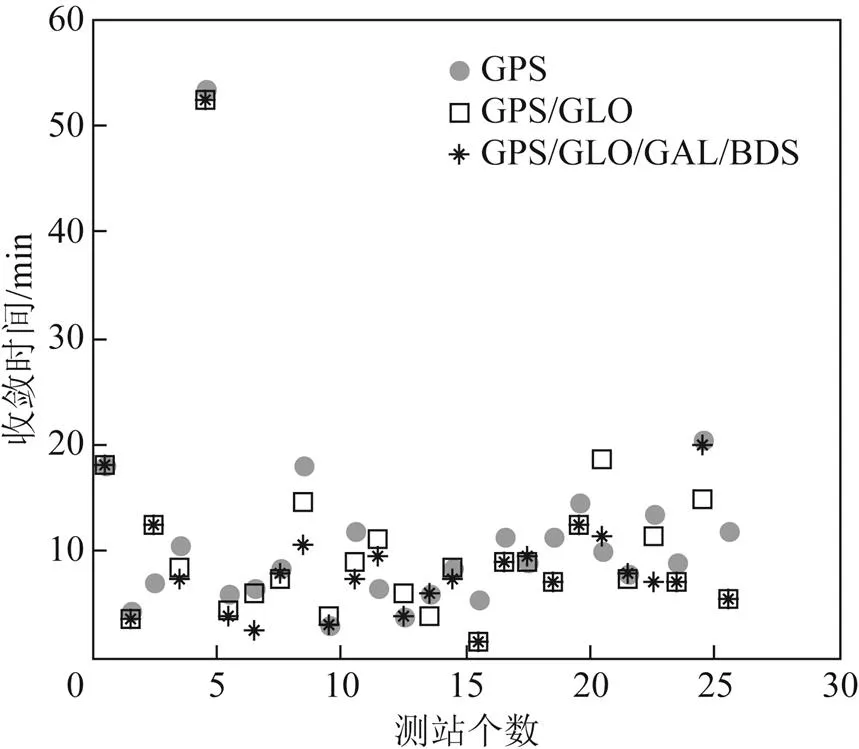
图2 各测站实时ZTD估值收敛时间

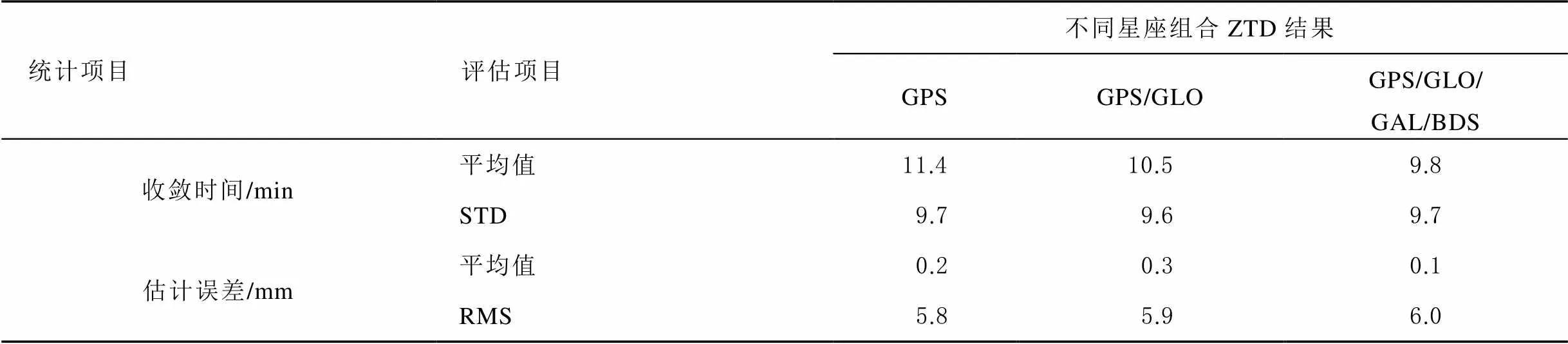
表3 实时ZTD估值收敛时间和估计误差统计值

图3给出了单历元实时ZTD估值误差的分布。需要注意的是，图3中并不包含处于收敛阶段的ZTD结果。对于3种不同的星座组合，ZTD误差均近似服从正太分布，但多系统组合情形中较小ZTD误差占比稍大。据统计，对于GPS单系统、GPS/GLONASS双系统和4系统组合PPP，误差小于5 mm的实时ZTD估值分别占比63.0 %、63.3 %和64.2 %。表3中也给出了实时ZTD估值误差的统计值。从表中可知，平均ZTD误差非常接近于0。根据RMS统计值，3种不同星座组合PPP实时ZTD估值精度在同一水平，分别为5.8、5.9、6.0 mm。

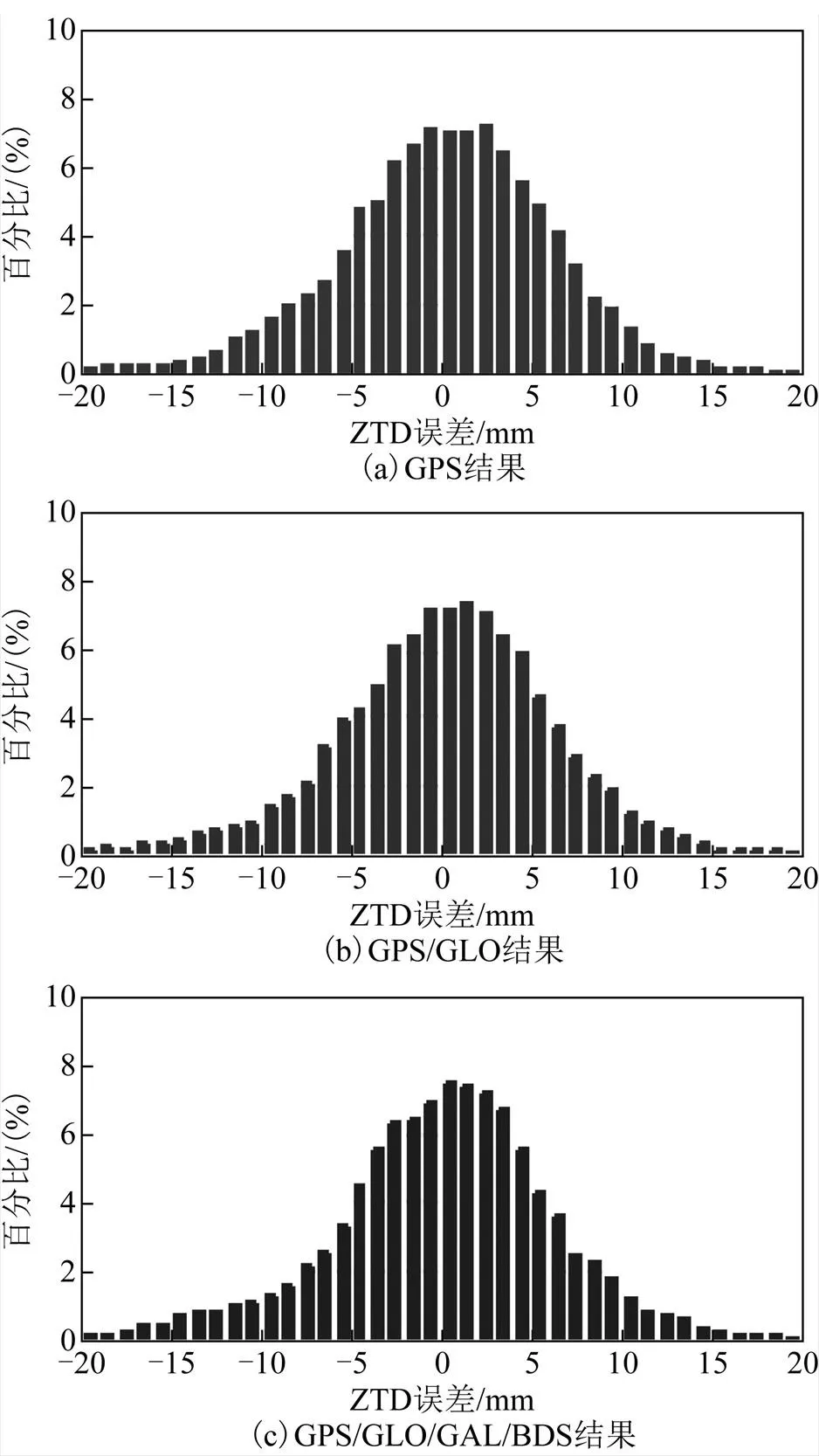
图3 单历元实时ZTD估值误差的分布

图4给出了实时PPP ZTD估值和后处理USNO ZTD产品之间的线性拟合。每个子图中还给出了互相关系数和线性回归函数。对于3种不同的星座组合，实时PPP ZTD和后处理USNO ZTD间的互相关系数均大约为1.000，表明二者之间存在强相关。

很多时候，大气参数获取需要在遮挡环境下进行，比如露天矿区、山区和城市峡谷。为了研究4系统组合PPP实时ZTD估计在卫星可见受限环境下的性能，将截止高度角增加到40°来简单模拟这些真实的恶劣环境。图5给出了截止高度角为40°时STR1站单历元实时ZTD估值误差。从图中可知，GPS单系统实时PPP在很多历元不能得到ZTD，尤其是在12:00—16:00。从总体来看，联合使用多星座信号减小了ZTD误差。为了进一步分析，表4给出了相应ZTD估值可用性和估计误差RMS值。可用性指的是能够获取实时ZTD历元数和总历元数之间的百分比。需要说明的是，所有ZTD估值均参与了表4中的精度统计，包括收敛阶段的结果。当截止高度角为40°时，GPS单系统情形可用性只有56.4%，而GPS/ GLONASS双系统情形可用性下降到91.1%，与二者相比，4系统组合情形可用性仍可以达到98.2%。和GPS单系统情形相比，GPS/GLONASS双系统情形实时ZTD估计精度从14.4提高到12.7 mm，在进一步引入Galileo和BDS观测值后，实时ZTD估计精度进一步提高到11.0 mm。

图4 实时PPP ZTD估值和后处理USNO ZTD产品之间的线性拟合

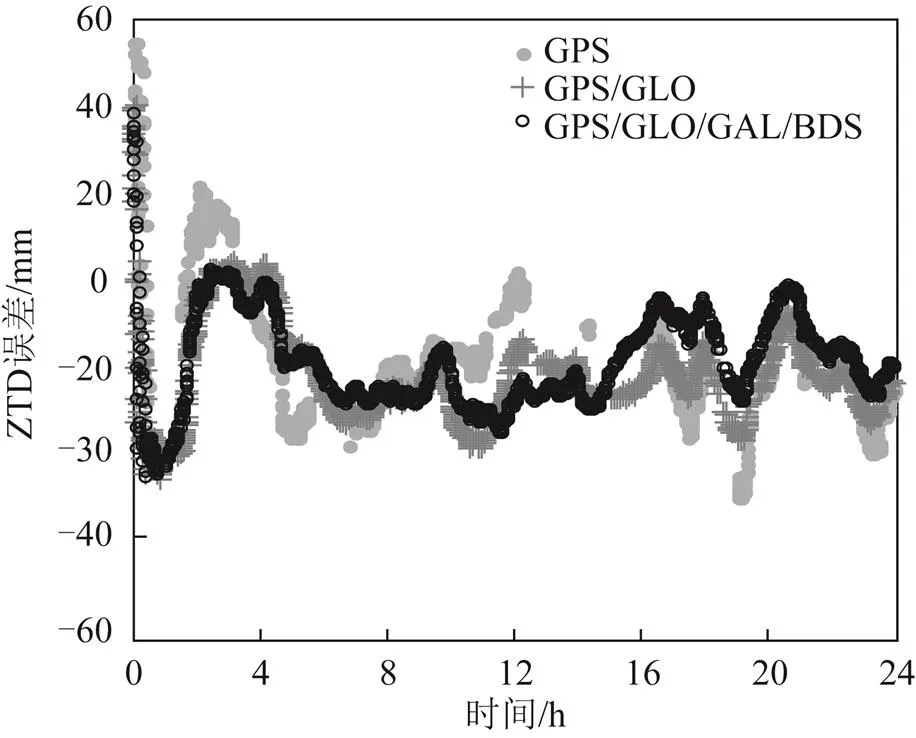
图5 截止高度角为40°时STR1站单历元实时ZTD估值误差

表4 截止高度角为40°时STR1站实时ZTD估值可用性和估计误差RMS值

在前面的处理中，均是利用IGS SINEX解固定了测站坐标。为了研究测站坐标处理策略对实时ZTD估计的影响，表5给出了估计测站坐标时GPS单系统PPP实时ZTD估值收敛时间和估计误差统计值，使用了全部26个MGEX站数据。测站坐标模拟为常数进行估计。比较表3和表5中结果可知，和固定测站坐标的实时ZTD估值相比，估计测站坐标的实时ZTD估值收敛时间延长了1.8 min，估计精度下降了0.2 mm。因此，在采用PPP技术进行实时ZTD估计时，建议使用高精度的已知坐标来改善实时ZTD估值性能。

表5 估计测站坐标时GPS单系统PPP实时ZTD估值收敛时间和估计误差统计值

为了研究所使用的精密卫星轨道和钟差产品对ZTD估计的影响，表6给出了不同星座组合PPP后处理ZTD估值收敛时间和估计误差统计值。采用GFZ最终精密卫星产品进行解算。比较表3和表6中结果可知，和实时PPP ZTD估值相比，单系统、双系统、4系统情形中后处理PPP ZTD估值收敛时间分别缩短了4.9、5.6、5.1 min，估计精度分别提高了0.5、0.4、0.3 mm。

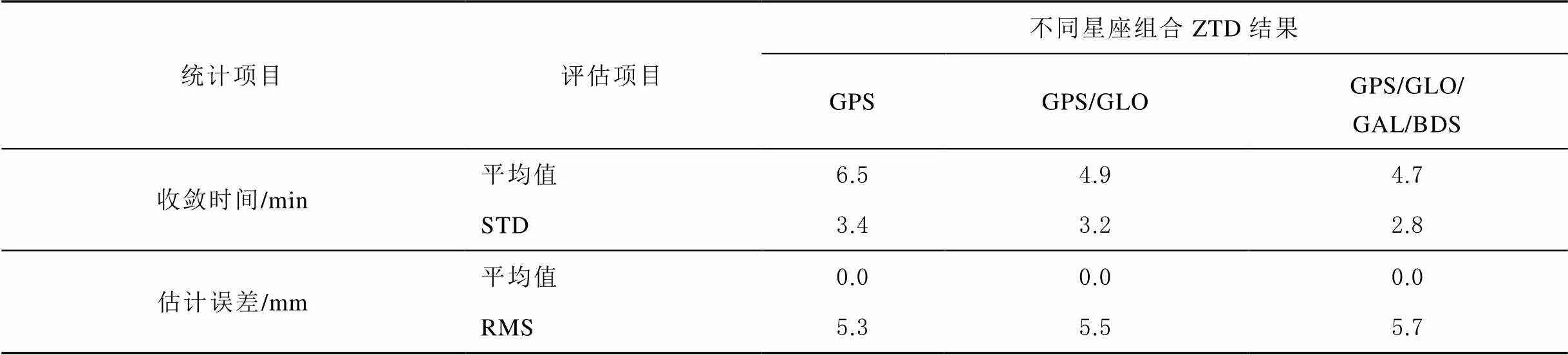
表6 不同星座组合PPP后处理ZTD估值收敛时间和估计误差统计值

3 结束语

本文提出了1种GPS/GLONASS/Galileo/BDS 4系统组合PPP实时估计ZTD方法。和GPS单系统以及GPS/GLONASS双系统结果相比，4系统组合PPP实时ZTD估值的收敛时间、估计精度和可用性均有所改善，尤其是在遮挡观测环境下（高截止高度角），因而可以更好地应用于气象学研究。评估了CNES提供的4系统实时精密卫星产品质量，从而确定了合适的观测值随机模型。和固定测站坐标的实时ZTD估值相比，估计测站坐标的实时ZTD估值性能下降，建议在解算时采用前1种策略。和后处理ZTD估值相比，实时ZTD估值的收敛时间明显偏长，估计精度也稍有下降。下一步工作是研究多频率融合PPP实时估计对流层延迟。

[1] BEVIS M, BUSINGER S, HERRING T, et al.GPS meteorology: remote sensing of atmospheric water vapor using GPS[J].Journal of Geophysical Research-Atmospheres, 1992, 97(D14): 15787-15801.

[2] GENDT G, DICK G, REIGBER C, et al.Near real time GPS water vapor monitoring for numerical weather prediction in Germany[J].Journal of the Meteorological Society of Japan, 2004, 82(1B): 361-370.

[3] KARABATIĆ A, WEBER R,HAIDEN T.Near real-time estimation of tropospheric water vapour content from ground based GNSS data and its potential contribution to weather now-casting in Austria[J]. Advances in Space Research, 2011, 47(10): 1691-1703.

[4] BENNITT G V,JUPP A.Operational assimilation of GPS zenith total delay observations into the met office numerical weather prediction models[J].Monthly Weather Review, 2012, 140(8): 2706-2719.

[5] BONIFACE K, DUCROCQ V, JAUBERT G, et al.Impact of high-resolution data assimilation of GPS zenith delay on Mediterranean heavy rainfall forecasting[J].Annales Geophysicae, 2009, 27(7): 2739-2753.

[6] SHOJI Y, KUNII M, SAITO K. Mesoscale data assimilation of Myanmar cyclone Nargis part II:assimilation of GPS-derived precipitable water vapor[J].Journal of the Meteorological Society of Japan, 2011, 89(1): 67-88.

[7] YAO Y B, SHAN L L, ZHAO Q Z. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application[EB/OL].[2018-10-18].https://www.nature.com/articles/s41598-017-12593-z.

[8] CAI C S, GAO Y, PAN L, et al.Precise point positioning with quad-constellations:GPS, BeiDou, GLONASS and Galileo[J].Advances in Space Research, 2015, 56(1): 133-143.

[9] PAN L, GUO F, MA F J.An improved BDS satellite-induced code bias correction model considering the consistency of multipath combinations[J].Remote Sensing,2018,10(8): 1189-1196.

[10] ZHOU F, DONG D N, GE M R,et al.Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations[J].GPS Solutions,2018,22(1):1-14.doi>10.1007/s10291-017-0685-7.

Real-time estimation of tropospheric delay with use of multi-constellation signals

XU Xiwen1, ZHANG Zhiwei1, LI Chenfeng2

（1. School of Surveying, Mapping and Geoinformation, Jiangxi College of Applied Technology, Ganzhou, Jiangxi 341000, China;2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China）

Aiming at the problems that it is difficult to be applied in the time-critical meteorology for the tropospheric delay obtained in the post-processing or near-real-time modes, and it is relatively poor of ZTD performance for GPS-only precise point positioning (PPP), the paper proposed a real-time estimation method of ZTD with the PPP integrated GPS, GLONASS, Galileo and BDS. Study results showed that: the convergence time for the PPP estimation of real-time zenith total delay (ZTD) derived from GPS-only, GPS/GLONASS and GPS/GLONASS/Galileo/BDS would be 11.4, 10.5 and 9.8 min respectively, and the corresponding estimation accuracy would be 5.8, 5.9 and 6.0 mm respectively, with an elevation mask angle of 7°; moreover, the availability of the real-time ZTD for the three different constellation combinations would be 56.4 %, 91.1 % and 98.2 % respectively, and the corresponding estimation accuracy would be 14.4, 12.7 and 11.0 mm respectively, with an elevation mask angle of 40°.

tropospheric delay; precise point positioning; convergence time; estimation accuracy; availability

P288

A

2095-4999(2019)03-0069-07

2018-11-07

武汉大学地球空间环境与大地测量教育部重点实验室开放基金资助项目（15-02-06）。

许锡文（1976—），男，江西吉安人，硕士，副教授，研究方向为GNSS精密定位及其地学应用。

李辰风（1990—），男，江西大余人，博士生，研究方向为GNSS精密定位及其地学应用。

许锡文，张志伟，李辰风.联合使用多星座信号实时估计对流层延迟[J].导航定位学报,2019,7(3):69-75.（XU Xiwen, ZHANG Zhiwei, LI Chenfeng.Real-time estimation of tropospheric delay with the use of multi-constellation signals[J].Journal of Navigation and Positioning,2019,7(3):69-75.）

10.16547/j.cnki.10-1096.20190312.