标签高度差的UWB室内定位方法

岳俊升，程 钢，邓 超

标签高度差的UWB室内定位方法

岳俊升1,2，程 钢1,2,3，邓 超2,3

（1. 河南理工大学 测绘与国土信息工程学院，河南 焦作 454000；2. 河南理工大学 矿山空间信息技术河南省重点实验室，河南 焦作 454000；3. 信息工程大学 地理空间信息学院，郑州 450001）

针对室内复杂定位场景中3维定位计算复杂度高、2维定位精度较低的问题，面向智慧仓储的物流车快速定位提出一种考虑高度差的超宽带室内定位算法，采用一种介于2、3维之间的2.5维到达时间差定位算法，利用泰勒级数展开法求解非线性观测值方程，得到标签的位置坐标。实验结果表明，通过在2维定位算法中增加高度差影响因子，能有效降低因标签与基站高度差异带来的2维定位误差和因3维解算效率低带来的定位延时，提高室内定位的准确性和实时性。

超宽带；室内定位；2.5维定位；高度差；定位误差

0 引言

随着地下空间、大型室内场馆等内部空间的开发和利用，人们对高精度和实时性的室内定位服务需求更加迫切。超宽带（ultra-wide band, UWB）技术[1]是一种中心频率大于500 MHz，使用脉冲宽度为纳秒或者皮秒的冲击波传输数据的信号传输技术，具有很高的传输速率、多径分辨率、时间分辨率和定位精度，利用其独特的通信机制和特点，可为室内位置服务提供很好的解决方案。目前，基于UWB的室内定位[2]在智能家居、智能仓储、智慧工厂等领域得到广泛应用，相关定位算法也取得很大进步。

在UWB定位系统中，定位方法分为以下几种：①圆周定位法即到达时间定位法（time of arrival, TOA）[3]，该定位方法需要基站与标签的时钟要精确同步，对硬件要求较高；②方位角测量定位法即到达角度定位法（angle of arrival, AOA）[4-5]，在复杂的定位场景中，易受到非视距（non-line-of-sight, NLOS）[6]的干扰影响定位精度；③双曲线定位法即到达时间差定位法（time difference of arrival, TDOA）[7]，只需要基站之间的时钟同步，具有容易实现、抗干扰能力较强的特点。上述定位方法中，待定位点位置坐标一般通过求解非线性方程来获取。关于非线性方程组的求解，很多学者提出了适用于不同定位场景，具有不同复杂性和定位精度的位置估计算法，比如：Fang算法，用3个基站进行定位；Chan算法[8]，在测量误差很小或服从理想高斯分布的情况下，可利用多余基站信息提高定位精度；最小二乘算法[9]，往往获取的是方程组的次优解。泰勒级数展开法[10]，采用迭代运算不断接近未知数的真实值，具有顽健性强、解算精度高的优点，是求解复杂、高阶非线性方程的有效方法。

大型智慧仓储系统需要对室内各类移动设备（如叉车等）进行准确定位和跟踪。为了基站统一管理、不妨碍正常生产线，提高设备定位的准确性和及时性，通常将基站和移动设备标签分别设置于统一的高处，基站位置高于移动标签位置。然而在实际应用中，为了简化计算过程，通常以牺牲精度为代价，忽略基站和设备标签之间的高度差。而理想的3维定位解算方法[11]将增加算法复杂度和定位服务器负担，牺牲大量解算时间，定位具有滞后性，降低了定位的实时性。

本文针对大型室内复杂场景移动设备定位的实际需求，提出一种基于高度差的UWB室内定位算法，通过在传统2维定位方法的基础上增加高度差影响因子，采用TDOA定位算法和泰勒级数展开法对室内移动设备进行位置解算，提高设备定位的准确性和实时性。

1 算法模型

基于UWB的定位算法[12]中，首先需要精确测量基站与标签的距离，通过建立观测方程来求解未知参数，得到标签的位置坐标。

1.1 基于高度差的TDOA定位算法

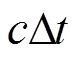
在实际定位场景中，基站和标签不在同一水平面上，而是处于3维立体空间中，基站和标签在空间的相对位置分布如图1所示。

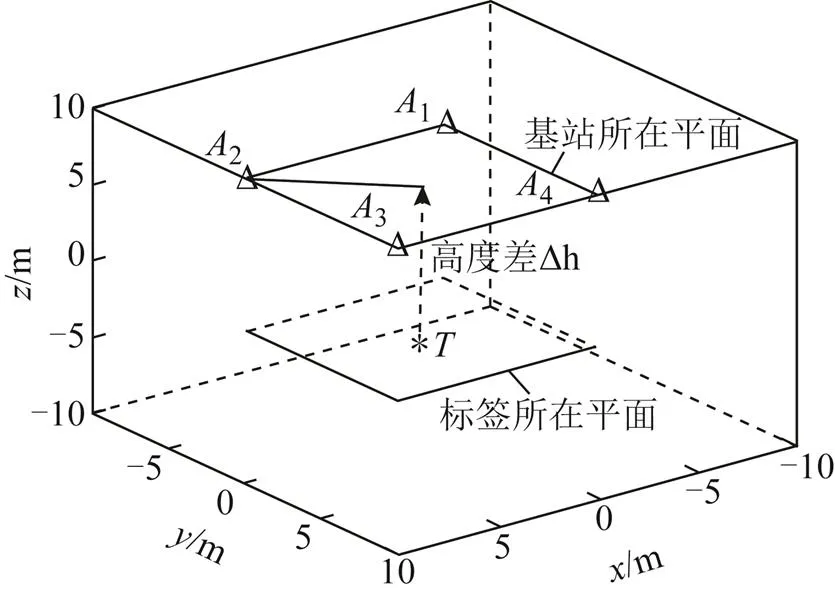
图1 定位基站与标签在3维空间中相对位置分布

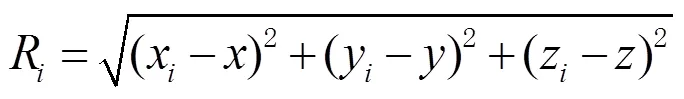
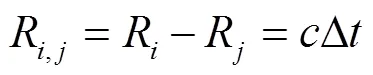
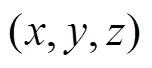
为了简化运算，传统2维定位中，假设定位基站与移动标签在同一个水平面内，依据TDOA定位原理，利用移动标签到达2个基站的距离差建立一条双曲线，根据不同双曲线的交点确定标签的位置，如图2所示。

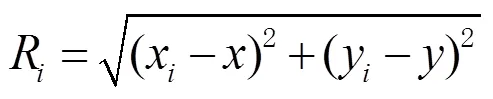
2维定位中，未知数个数减少，需要的观测量也减少，降低了解算复杂度；但由于忽略基站与标签之间的高度差，降低了定位精度。

大型智慧仓储系统[13-15]为了基站的统一管理、不妨碍正常生产线，同时提高设备定位的准确性和及时性，通常将基站和移动设备标签分别设置于统一的高度。考虑到标签与基站所在平面的高度差固定不变，本文提出一种2.5维的室内定位模型。该模型根据实际场景，将标签与基站的高度差设置为常数，则式（3）可以转化为

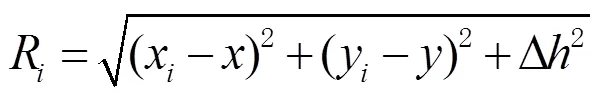
1.2 泰勒级数展开法模型

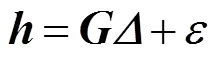
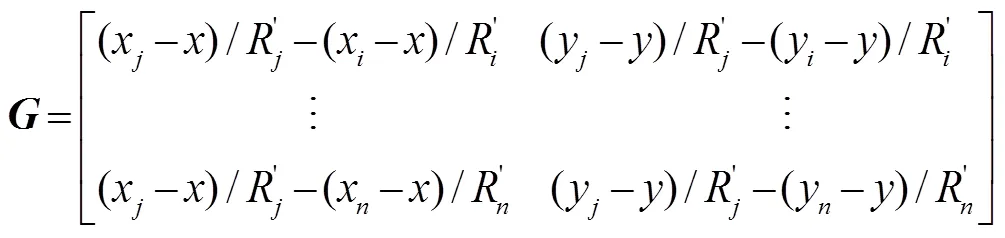
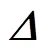
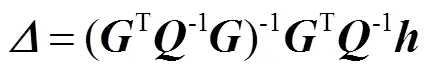
式中为TDOA测量值的协方差矩阵。通过式（6）可以得到下次迭代的初始值，将该值代入式（2）进行下一轮的泰勒级数展开，下次迭代的初始值为

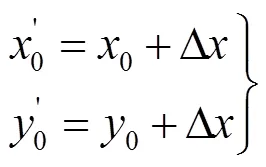
2 实验及结果分析

2.1 实验设置

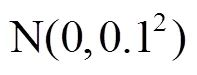
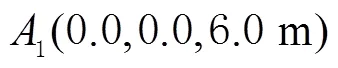
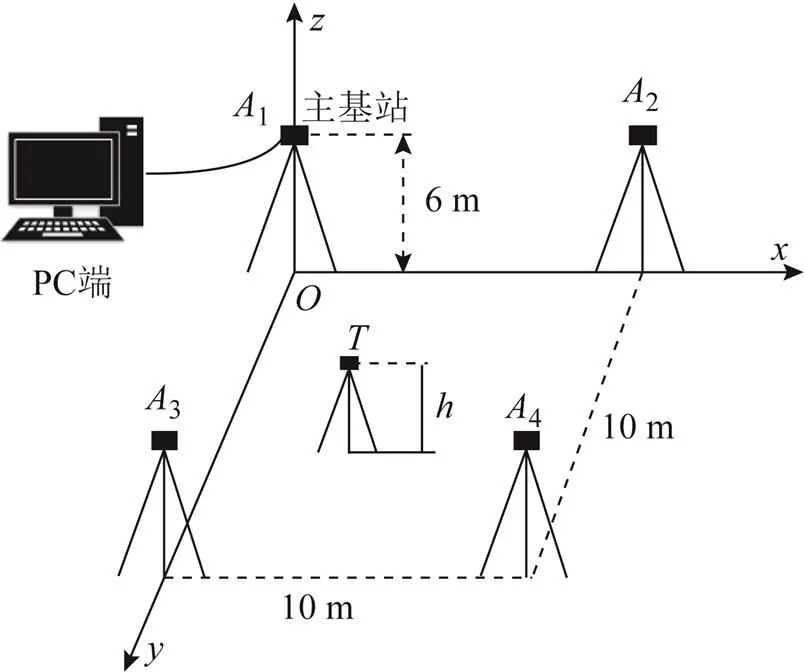
图3 实验环境的空间坐标系及定位基站的分布

为了验证高度差对定位误差及实时性的影响，本实验分别计算了定位标签在每个网格顶点不同高度处的定位误差并记录了算法迭代次数。

2.2 结果分析

2.2.1 整体误差与实时性分析

实验通过对比是否增加高度差影响因子来获取实验区域中每个网格顶点不同高度差处的标签定位结果，分析高度差对定位精度和实时性的影响及其整体分布规律。不同高度差的水平定位误差分布如图4所示。

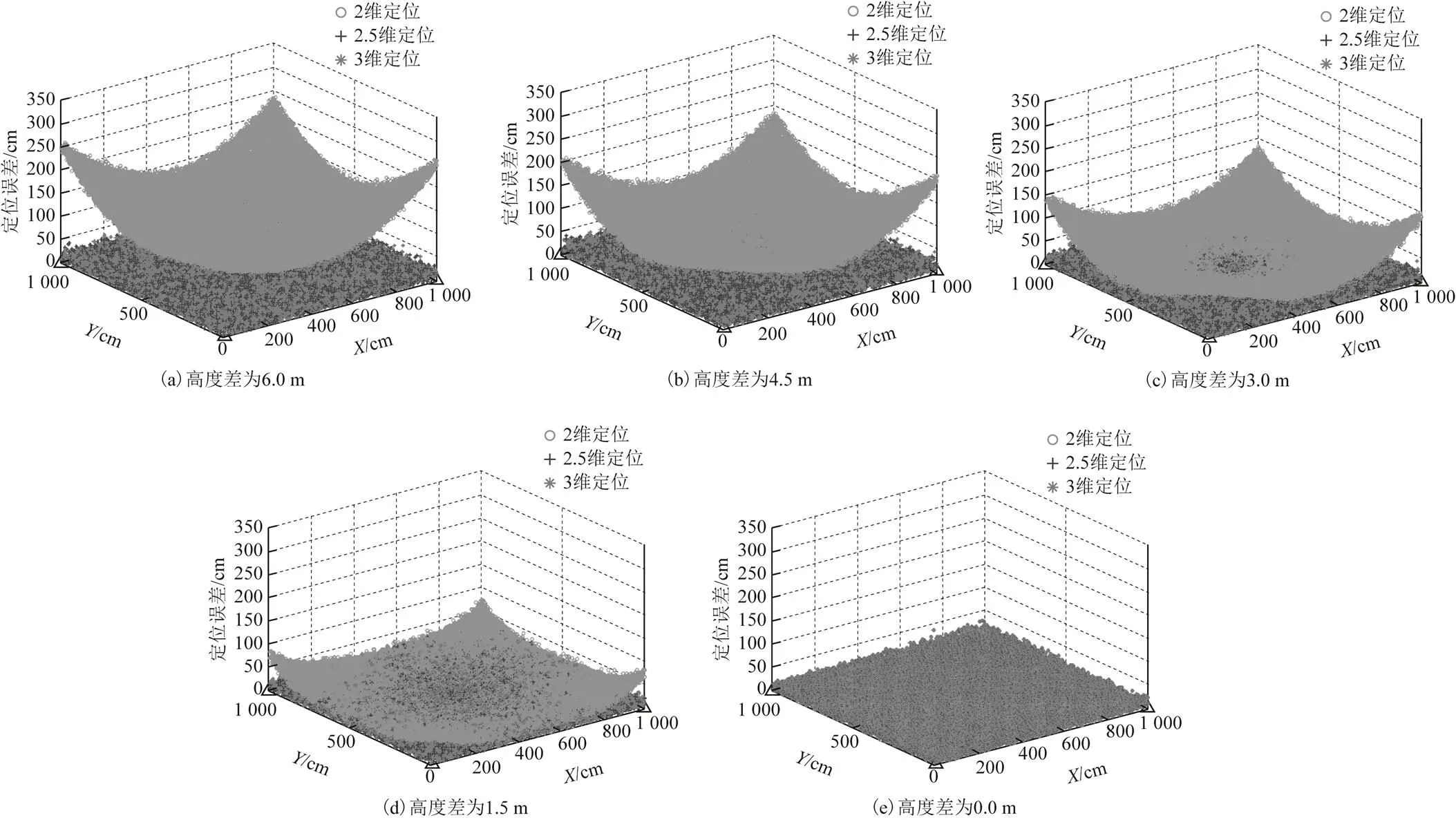
图4 标签在不同高度差处水平误差分布

由整体水平误差分布图可知，标签在2维定位场景中的误差分布呈现一定对称性，越接近定位区域的中心位置定位误差越小：在定位区域的基站位置，即4个顶点处误差达到最大值；在不同高度处，2维定位误差随着高度差的增加而增大。在2维定位算法中增加高度差影响因子，能够消除高度差对定位精度的影响，定位精度与3维定位精度相当；当标签与基站在同一个平面上时，即高度差为0.0 m，高度差对定位精度没有影响。

通过对同一高度差所有网格顶点处标签定位误差和运算迭代次数进行平均，得到不同高度差定位结果对应的标签定位平均水平误差与平均迭代次数，如表1所示。

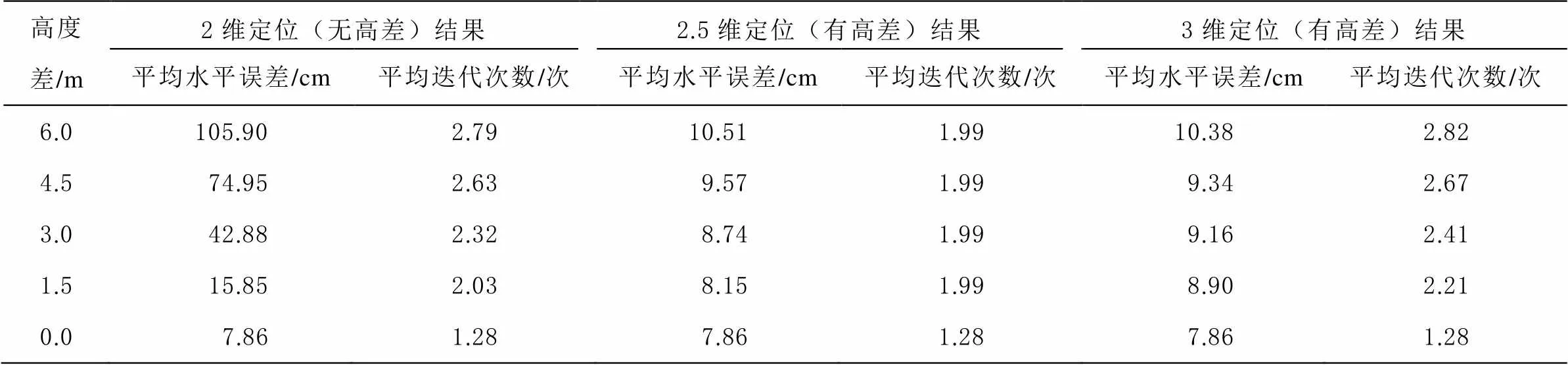
表1 标签整体平均水平误差与迭代次数分布

由表1可知，标签的平均水平误差与平均迭代次数随着高度差的增加而增加。对同一高度差处的标签进行定位，本文提出的定位方法比2维定位更精确，比3维定位迭代次数更少。实验说明，在复杂的定位场景中增加高度差影响因子的2.5维定位，能够提高区域整体定位精度和实时性。

2.2.2 局部误差与实时性分析

图5 单个网格点在不同高度差处估计位置散点分布

由单个网格点的估计位置与实际位置散点分布图可知，忽略定位标签与基站之间的高度差的2维定位方法会使标签的估计位置偏离实际位置。本文提出的2.5维定位方法能够使标签的估计位置逐渐逼近其真实位置，定位精度优于2维定位算法，与3维定位精度相当。

将2维定位和本文定位方法的定位误差进行统计，得到误差的累积分布函数（cumulative distribution function, CDF），如图6所示。其中横坐标为定位误差，纵坐标为小于等于某个定位误差下的定位次数在总定位次数中的百分比。一般可以将累积概率大于或等于95%时对应的横坐标定位误差值作为本次实验的定位精度。

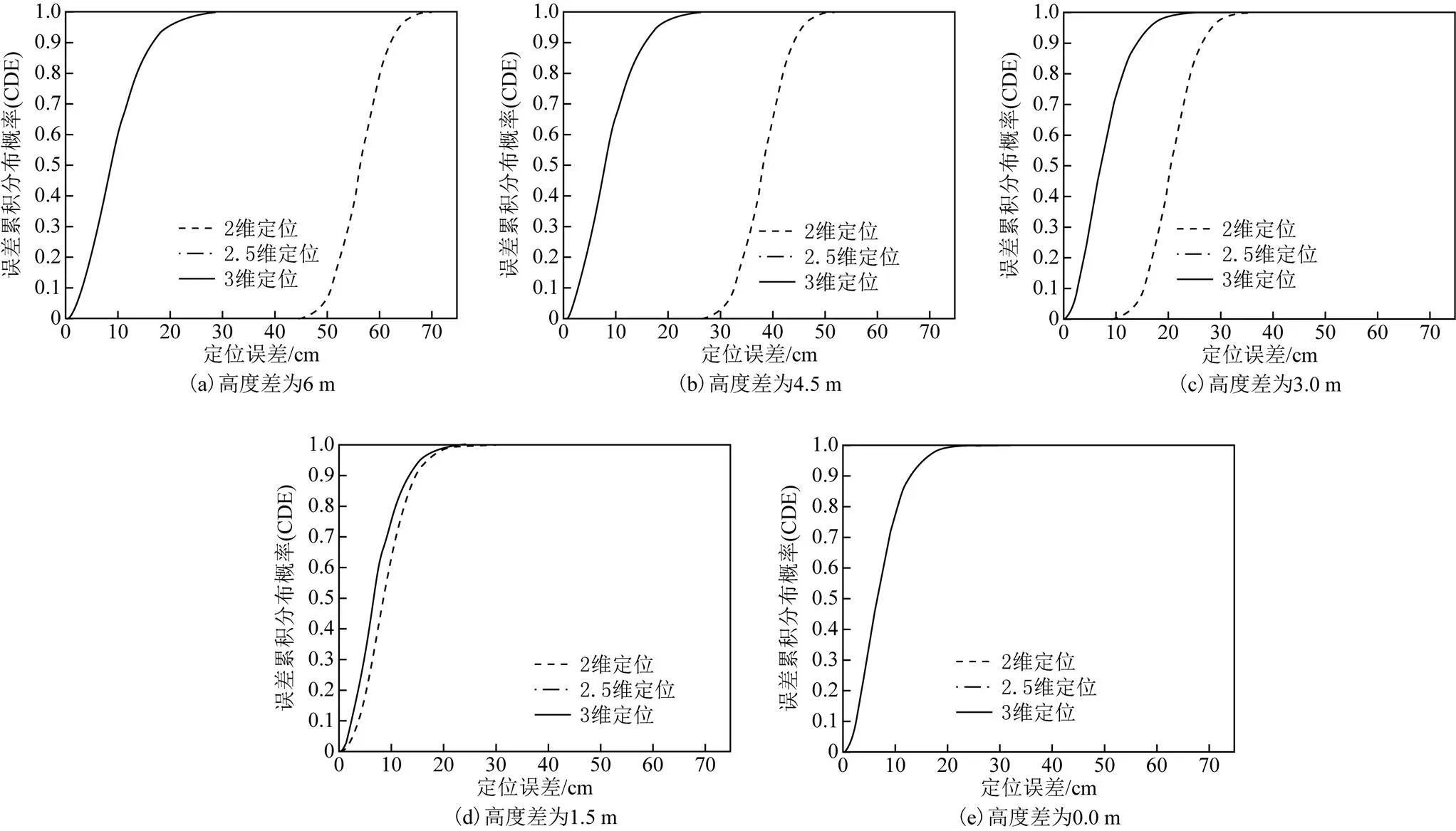
图6 单个网格点在不同高度差处定位误差CDF分布

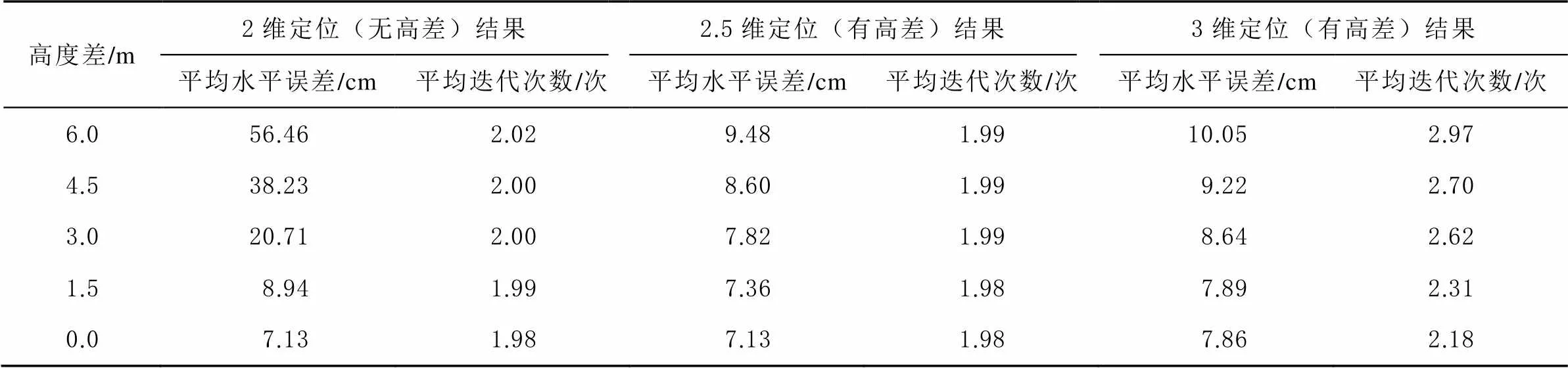
表2 单个网格点标签的水平误差与平均迭代次数分布

由表2可知，对于单个网格点处的标签而言，在定位算法中增加高度差因子可以显著提高定位精度，纠正由于忽略高度差而带来的系统误差，提高定位准确性。这种改进，随高度差的增大而效果更加明显。同时，通过与3维定位结果对比，增加高度差影响因子定位精度与3维定位相当，但能够明显减小算法迭代次数，提高定位实时性。

3 结束语

本文面向复杂场景UWB室内定位中3维定位复杂度高、2维定位精度较差等问题进行了研究。对较为常用的定位模型和解算方法进行了系统分析和对比，并以智慧仓储为应用场景，提出了一种考虑基站和标签高度差的改进的TDOA定位方法和基于泰勒级数展开的位置求解方法。通过仿真实验对定位方法和求解算法进行了模拟，对不同定位方法下误差的分布规律和解算的实时性进行了对比分析。精度方面，单点和整体网格点的定位精度优于10 cm，且相对于2维定位方法，精度具有良好的稳定性，不随高差的变化而变化；解算效率方面，单点平均解算迭代次数小于2次，明显优于3维定位方法的解算速度。仿真实验证明了经过改进的TDOA定位方法具有较好的定位精度和解算速度，实用性较好。后续将对算法进行移植，并在实际环境中进行应用。

[1] 童凯翔, 周轩, 李广侠, 等. 超宽带在无线定位技术中的应用综述[J]. 导航定位学报, 2015, 3(1): 10-14.

[2] 李自良, 韩笑, 李硕, 等. 基于超宽带的室内定位技术[J]. 数字通信世界, 2018(8): 40-42.

[3] 王长强, 徐爱功, 隋心. 超宽带双向到达时间测距的室内动态定位方法[J]. 测绘科学, 2017, 42(12): 151-156.

[4] 马婧. 基于UWB信号的单基站定位算法研究及AOA定位研究[D]. 青岛: 中国海洋大学, 2013.

[5] 邹艳玲, 程爱华. 超宽带室内环境下的TDOA/AOA定位系统[J]. 微计算机信息, 2008(33): 164-166.

[6] HO K, YOUNG P. NLOS identification in UWB channel for indoor position[C]//The Institute of Electrical and Electronic Engineers(IEEE). Proceedings of 201815th IEEE Annual Consumer Communications & Networking Conference (CCNC). Las Vegas, Nevada: IEEE, 2018: 1-4.

[7] 卞佳兴, 朱荣, 陈玄. 基于改进双向测距-到达时间差定位算法的超宽带定位系统[J]. 计算机应用, 2017, 37(9): 2496-2501.

[8] 刘国栋. 基于UWB的室内定位技术研究[D]. 南京: 南京邮电大学, 2014.

[9] CHEUNG K W, SO H C. Least squares algorithms for time-of-arrival-based mobile location[J]. IEEE Transactions on Signal Processing, 2004(4): 1-8.

[10] 周康磊, 毛永毅. 基于残差加权的Taylor级数展开TDOA无线定位算法[J]. 西安邮电学院学报, 2010, 15(3): 10-13.

[11] 李倩宇, 李英祥, 吴珊, 等. 抗非视距的室内三维定位方法[J]. 系统仿真技术, 2018, 14(2): 118-122.

[12] JING Wang, YAO Tang. An improved indoor localization solution using a hybrid UWB-Doppler system with Kalman filter[C]//The Institute of Electrical and Electronic Engineers(IEEE). Proceedings of 2018 IEEE Radio and Wireless Symposium(RWS). Anaheim, California：IEEE, 2018: 181-183.

[13] 李纲, 韩秋英. 基于RFID的仓储货物精确定位方法研究[J]. 信息技术与信息化, 2014(8): 125-126.

[14] 仇皓麟, 刘阳, 张坤, 等. 基于RFID技术的智能仓储管理系统设计[J]. 科技创新导报, 2017, 14(5): 94-95.

[15] LIN Xing. Design and realization of the logistic storage temperature control unified information system based on internet of things[C]//The Institute of Electrical and Electronic Engineers(IEEE). Proceedings of 2011 International Conference on Business Management and Electronic Information. Guangzhou, China: IEEE, 2011: 32-35.

UWB indoor positioning method considering difference of height

YUE Junsheng1,2,CHENG Gang1,2,3, DENG Chao2,3

（1. School of Surveying and Mapping and Land Information Engineering, Henan Polytechnic University, Jiaozuo, Henan 454000, China;2. Henan Provincial Key Laboratory of Mine Space Information Technology, Henan Polytechnic University, Jiaozuo, Henan 454000, China;3.School of Geospatial Information, Information Engineering University, Zhengzhou 450001, China）

Aiming at the problems of the high computational complexity of three-dimensional positioning and the low precision of two-dimensional positioning in complex indoor positioning scenarios, the paper proposed a UWB indoor positioning algorithm considering the difference in height for the rapid positioning of logistics vehicles oriented to intelligent storage: a 2.5 dimensional time difference of arrival (TDOA) positioning algorithm was adopted, and Taylor series expansion method was used to solve the nonlinear observation equation; then the position coordinates of tags were obtained. Experimental result showed that the proposed method could effectively reduce the two-dimensional positioning errors caused by the difference between the tag and the base station height and the localization delay caused by the low efficiency of three-dimensional solution by adding the influence factor of height difference in the two-dimensional localization algorithm, and improve the accuracy and real-time of indoor positioning.

ultra-wide band; indoor positioning; 2.5 dimensional positioning; height difference; positioning error

P228

A

2095-4999(2019)03-0044-07

2018-11-08

国家自然科学基金资助项目(41001226)；中国博士后科学基金面上资助项目（2015M582831）；北部湾环境演变与资源利用教育部重点实验室开放基金项目（2014ESPKF08）；教育部人文社会科学研究青年基金项目（15YJCZH018）；河南省科技攻关项目（162102210063）；河南省高等学校骨干教师资助计划项目（2012GGJS-055）。

岳俊升（1991—），男，河南信阳人，硕士生，研究方向为地理信息科学方法与应用。

程钢（1981—），男，河南焦作人，博士，教授，研究方向为GIS理论与方法。

岳俊升，程钢，邓超.标签高度差的UWB室内定位方法[J].导航定位学报,2019,7(3):44-50.（YUE Junsheng,CHENG Gang,DENG Chao.UWB indoor positioning method considering difference of height[J].Journal of Navigation and Positioning,2019,7(3):44-50.）

10.16547/j.cnki.10-1096.20190308.