中国大陆IGS基准站基线时间序列噪声分析

吉长东，沈祎凡，王 强

中国大陆IGS基准站基线时间序列噪声分析

吉长东，沈祎凡，王 强

（辽宁工程技术大学，辽宁 阜新 123000）

针对基线时间序列中信号与噪声难分离的问题，提出一种确定最优噪声模型的方法：利用幂律模型（PLM）与极大似然估计（MLE）相结合的方法，求出3维坐标向量的功率谱指数和最大似然估计值，确定出最优噪声模型；然后利用中国大陆6个IGS站6 a的观测数据进行实验。结果表明：基线时间序列存在白噪声（WN）、闪烁噪声（FN）和随机漫步噪声(RWN)；方向的情况为，当基线长度在1015~2500 km之间时，主要为WN+FN，当基线长度大于2500 km且小于3225 km时，则为WN+FN+RWN，且RWN占43.09 %；和方向最优噪声模型分别为WN+RWN与WN+FN，并且RWN与FN分别占62.11 %和89.88 %。

全球卫星导航系统（GNSS）；国际GNSS服务组织（IGS）基准站；基线时间序列；谱指数；极大似然估计；噪声模型

0 引言

迄今为止，我国的基于全球卫星导航系统（global navigation satellite system, GNSS）连续运行参考站（continuously operating reference stations, CORS）累积了大量的观测数据，由CORS数据解算出的基线和坐标的时间序列均可用于分析地球物理现象。鉴于基线时间序列受共模误差影响较小，基线时间序列分析优于坐标时间序列分析，为地球板块速度场、分析地震和预报地震等研究提供了数据基础[1]。

国内外许多专家学者在坐标时间序列方面做了大量的研究工作，并分析出其中的噪声成分；但短基线时间序列噪声分析方面研究较少，长基线时间序列噪声分析方面暂无相关研究。文献[2-5]解算国际GNSS服务组织（International GNSS Service, IGS）提供的观测文件，通过研究发现坐标时间序列中存在白噪声（white noise，WN）和有色噪声（color noise, CN），且时间跨度对噪声成分的影响较大[6]。利用经验模态分解方法分析IGS垂向具有年周期和半年周期的非线性运动，并利用谱指数和极大似然估计（maximum likelihood estimation, MLE）的方法分析出IGS测站高程时间序列中主要存在闪烁噪声（flicker noise, FN），随机漫步噪声（random walk noise, RWN）对其的影响较小[7]。分析了地震对基线时间序列在、、方向及基线长度造成的影响，且基线时间序列可表现出孕震信息，并基本不受共模误差影响[8-9]。利用极大似然估计方法分析了短基线时间序列的噪声成分，且分析了季节性及振幅对基线时间序列的影响[10]。为此，本文选取长度介于1015~3225 km之间的9条基线进行研究，分析其噪声模型及各类噪声所占比重，丰富任意长度基线时间序列的研究内容。

1 噪声分析方法

目前，噪声分析方法有经验估计、频谱估计、极大似然估计和范数二次无偏估计等[11]方法，而全球定位系统（global positioning system, GPS）时间序列噪声分析多采用频谱估计和极大似然估计方法（maximum likelihood estimate, MLE）。

1.1 谱指数法

GPS基线时间序列噪声一般呈幂律性的特点，用幂律模型中的谱指数来定性地描述其噪声成分[12-13]，幂律模型为

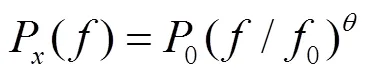
式中：P()为功率谱密度；0为基线时间序列常态下功率；0为基线时间序列中常态下频率；为谱指数。

当=0时，时间序列中存在高斯白噪声（WN）；当=-1时，基线时间序列存在闪烁噪声（FN）；当=-2时，基线时间序列存在随机漫步噪声（RWN）。当≠0，则基线时间序列表现为有色噪声特性，且谱指数值不同，具有不同噪声特性。

1.2 极大似然估计法

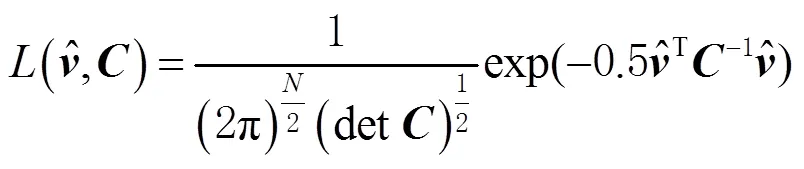
在基线时间序列分析时，对应速度项等是有偏的；若基线时间序列有足够长的数据，偏差是可以忽略的。残差时间序列一般是白噪声和几种有色噪声相叠加，对式（2）两侧取对数得

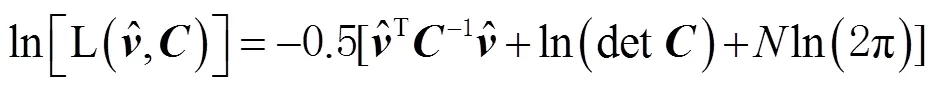
利用式（3）对多种噪声模型叠加求其极大似然估计值，便可确定最佳噪声模型；MLE越大说明噪声模型越接近真实的噪声模型[14-15]。当噪声模型越多时，极大似然值也会变大，所以不能只通过MLE大小来判断模型的优劣[16]。

1.3 最优模型确立准则

利用Langbein提出的保守估计准则[17]，首先假设基线时间序列中存在WN作为零假设，再求出WN+FN、WN+RWN下的MLE值，若其与零假设下的MLE差值大于阀值2.6，拒绝零假设，反之零假设成立。当WN+FN、WN+RWN下的MLE值与零假设下的差值均大于2.6，则选取MLE大的为最优噪声模型。接受WN+FN+RWN下的阀值为5.2。

2 基线残差时间序列

2.1 实验概述

实验选用中国大陆LHAZ、URUM、SHAO、BJFS、WUHN和KUNM 6个IGS基准站2008—2013年的观测数据。采用GAMIT/GLOBK软件解算各IGS站之间的基线，然后提取其对应的基线时间序列，最后利用MATLAB求出基线残差时间序列，选取长度在1015~3225 km之间的9条基线进行噪声分析。首先求出各基线3维分量的谱指数，并确定其噪声成分，然后利用CATS软件对基线残差时间序列进行噪声分析，并求出对应的MLE值，最后根据Langbein保守估计准则确定最优噪声模型。

2.2 时间序列获取

基线的每日解是由初始基线向量、基线速度项、周期波动、同震跳动和残差所构成的，其计算模型为

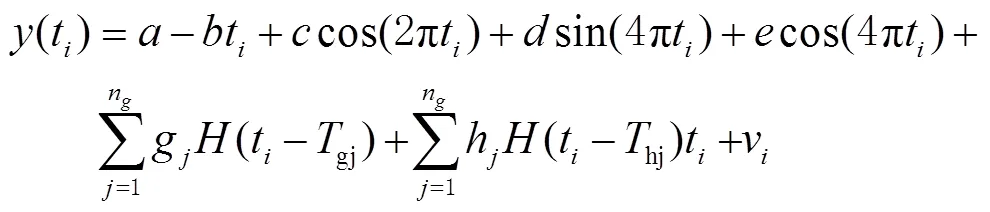
式中：(t)为第个历元的基线分量；为基线初始基线分量；为线性速度；为周年运行系数；、为半年运动系数；t为历元；为同震跳动；为震后变化速率；为阶梯函数；v代表基线向量的残差。

实验中9条基线的3维向量残差时间序列见图1至图9。

图1 LHAZ-BJFS基线残差时间序列

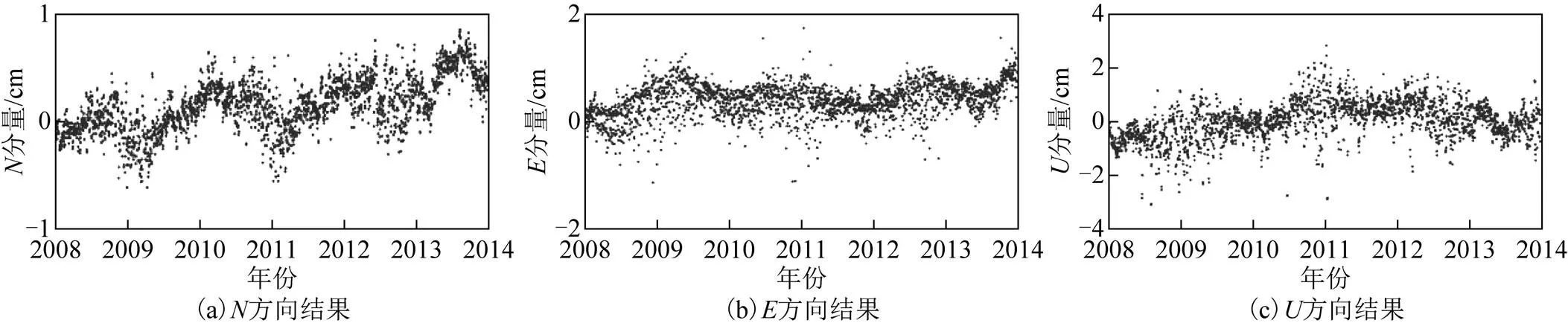
图2 BJFS-SHAO基线残差时间序列

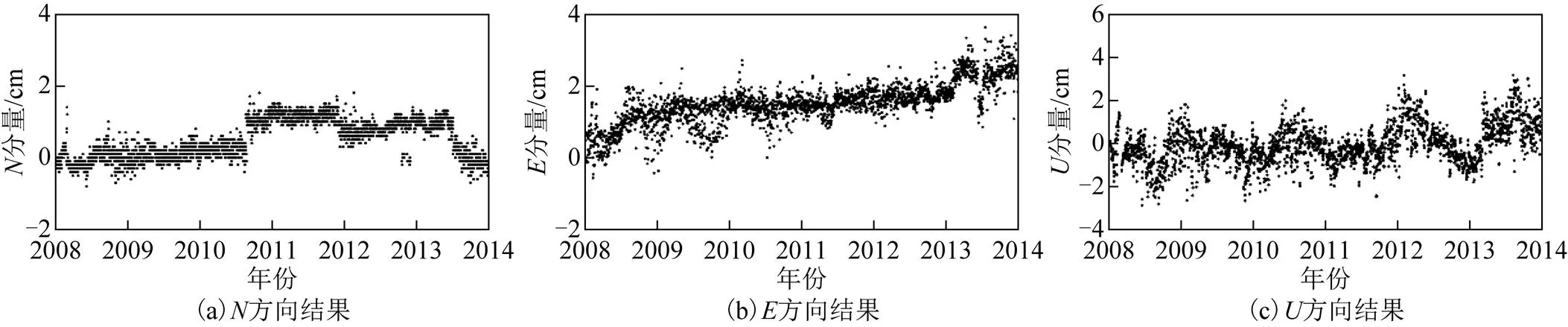
图3 BJFS-WUHN基线残差时间序列

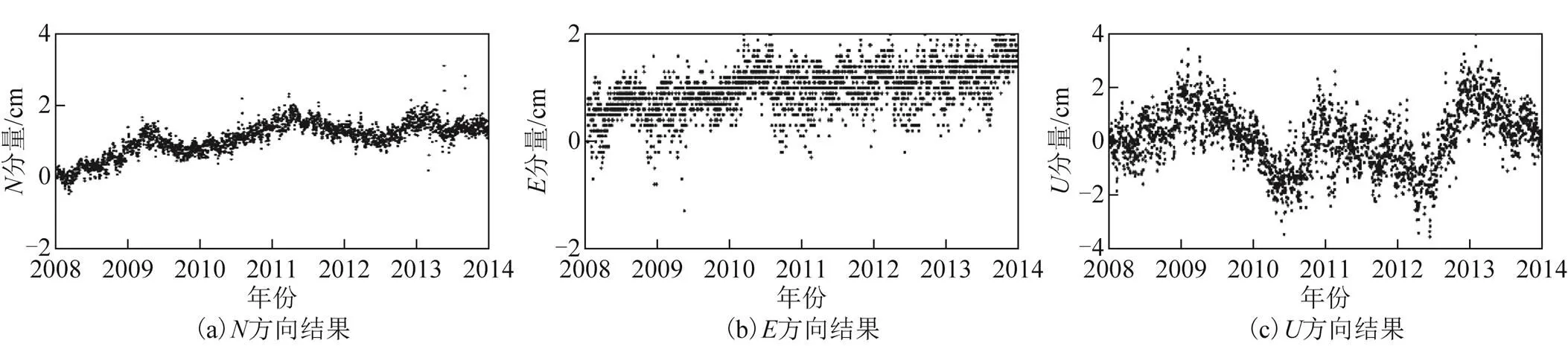
图4 SHAO-KUNM基线残差时间序列

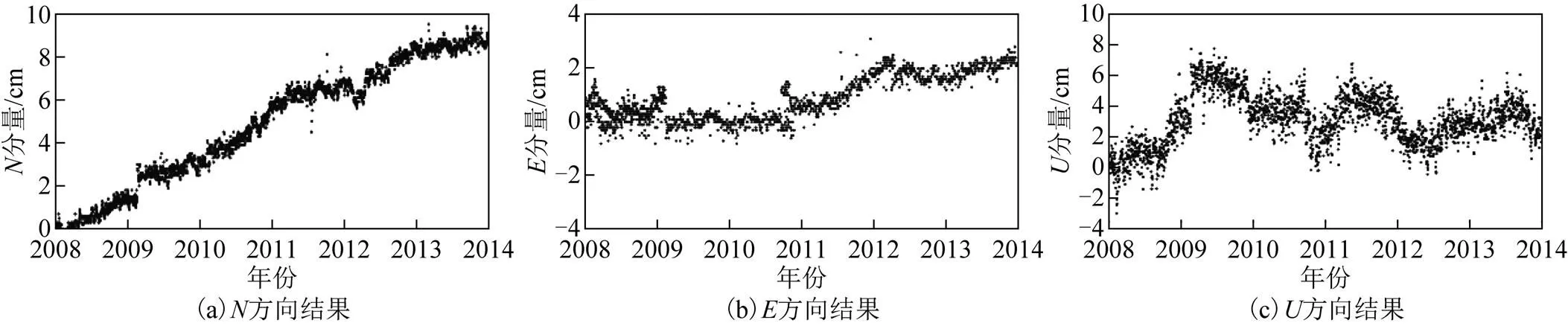
图5 URUM-KUNM基线残差时间序列

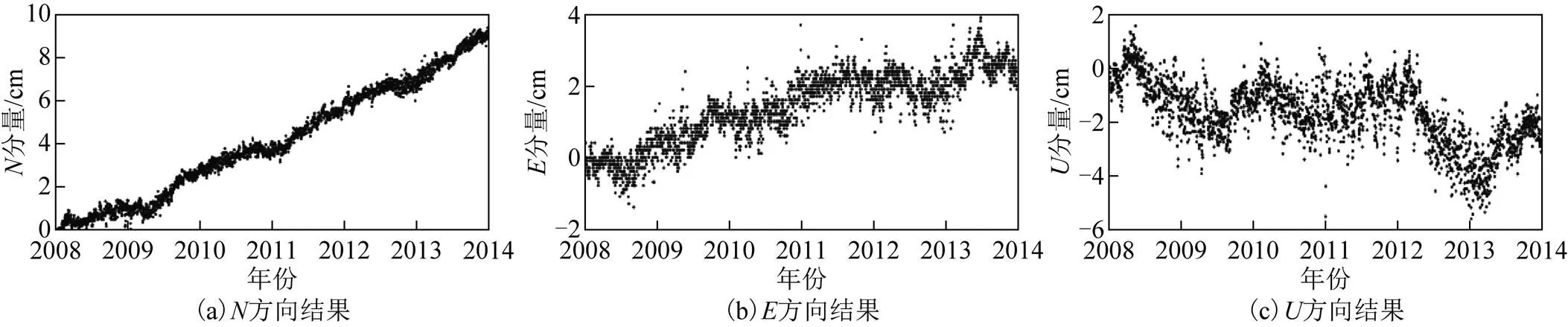
图6 LHAZ-SHAO基线残差时间序列

图7 LHAZ-URUM基线残差时间序列

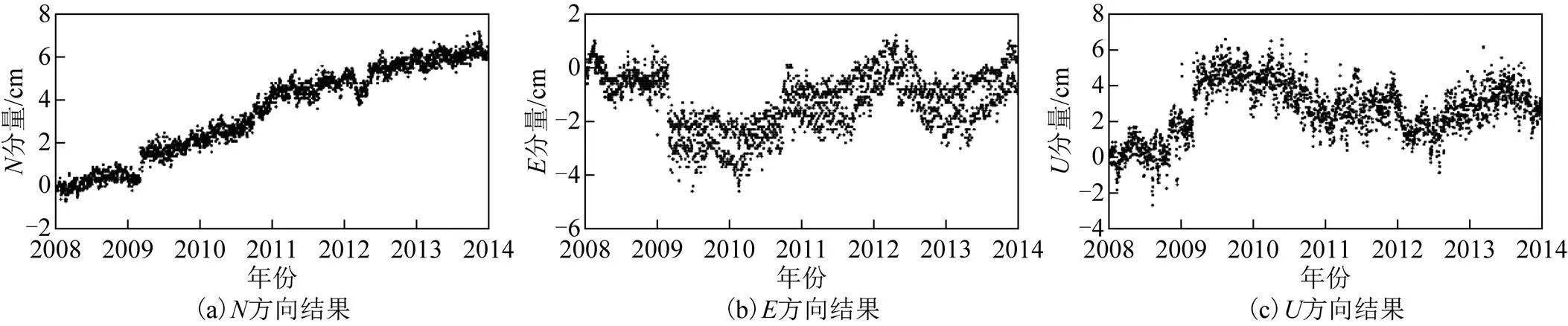
图8 URUM-SHAO基线残差时间序列

图9 URUM-WUHN基线残差时间序列

由图1至图9可知：在、方向上有线性的运动趋势，方向上呈非线性的运动趋势；并且可以看出基线时间序列的周年项及半周年项；在URUM-SHAO和URUM-KUNM基线残差时间序列中，、、方向在2009年2月附近有明显的阶跃现象，其原因可能是2009年2月20日新疆维吾尔族自治区阿克苏地区柯坪县发生5.2级地震，对基线时间序列、、方向都产生不同程度的影响。URUM-WUHN基线的方向在2010年5月附近有明显的阶跃现象，其原因可能是2010年4月17日西藏自治区那曲地区发生5.2级地震，导致方向有20 mm的跃动。

3 基线时间序列噪声模型分析

3.1 谱指数计算

利用周期图估计法求出每条基线3维分量的谱指数，并根据谱指数大小来判断基线时间序列噪声成分，谱指数值见表1。

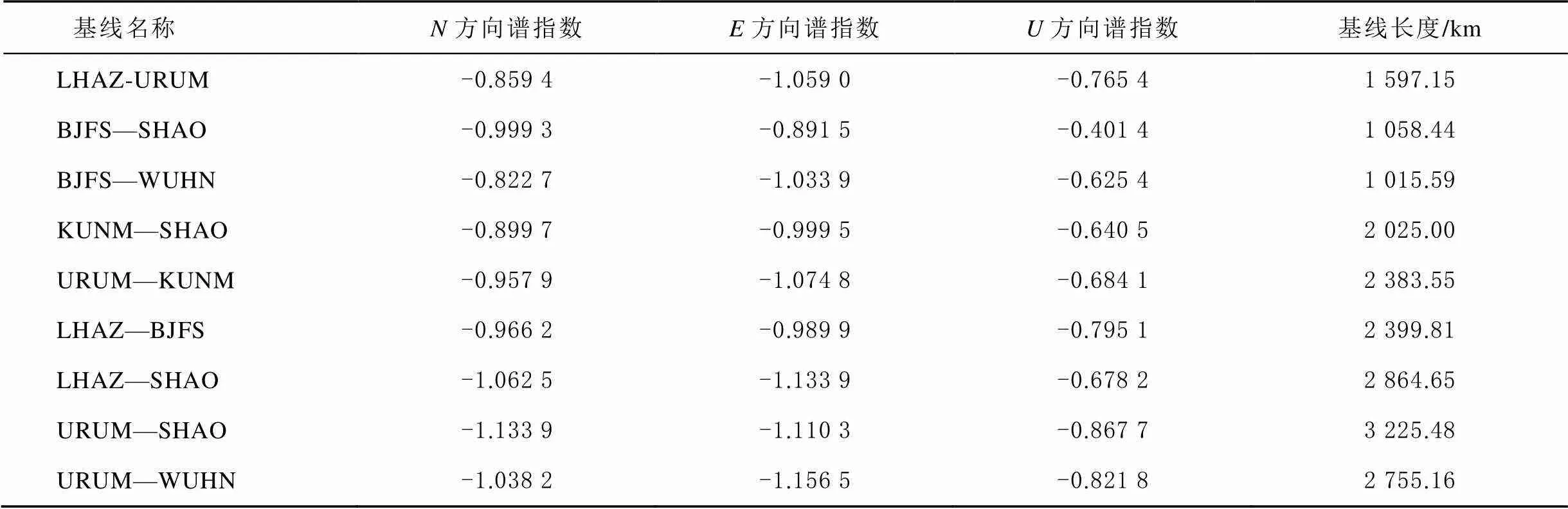
表1 各基线3维分量谱指数和基线长度

由表可知：、方向，谱指数在-2~0之间，存在白噪声、闪烁噪声和随机漫步噪声等；方向，谱指数值介于-1~0之间，存在白噪声和闪烁噪声。

3.2 噪声模型分析

根据各基线3维分量时间序列谱指数值判断出大致噪声类型，优选基线时间序列的最佳噪声模型。假设噪声类型有3种，即WN、FN和RWN。假定噪声组合类型有3种，即WN、WN+FN、WN+RWN及WN+FN+RWN。算出每种噪声模型下的极大似然估计，然后计算出每种噪声参数估值。并利用叠加的噪声模型算出的极大似然估计与白噪声下的极大似然估计之差（如见图10所示）。

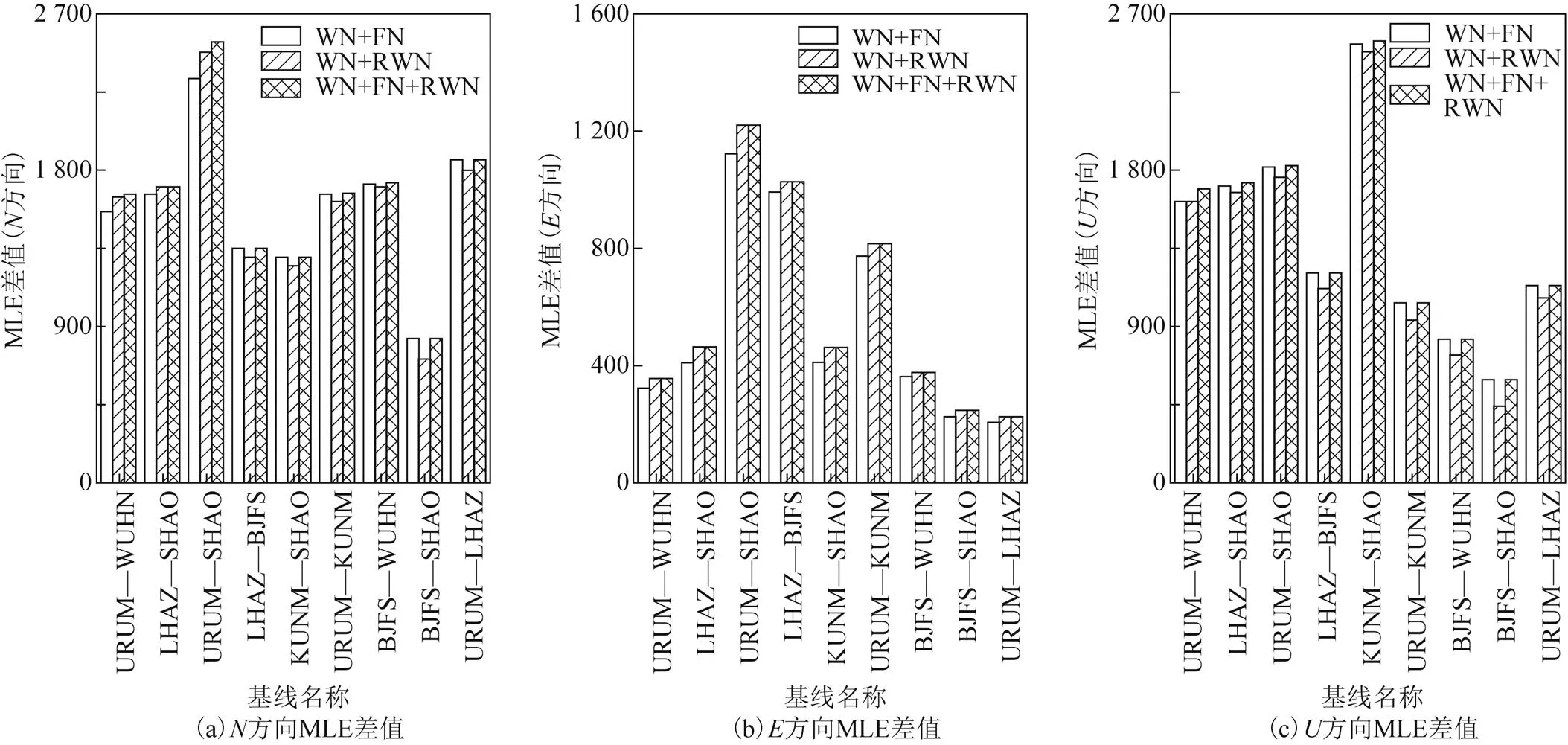
图10 基线N、E、U方向MLE差值

由图可知：方向，当基线长度小于2500 km时，由于WN+FN与WN+RWN的MLE值近似相等，都大于WN+RWN噪声模型的MLE值，当基线长度大于2500 km时，RWN的噪声强度增强，WN+FN+RWN与WN+RWN的MLE值近似相等，且在URUM—SHAO基线的RWN噪声强度显著增强；方向，所有基线的WN+FN+RWN与WN+RWN的MLE值基本相同；方向，除URUM—WUHN以外，所有基线的WN+FN与WN+FN+RWN的MLE值大致相同，而WN+FN+RWN的MLE值明显大于其他2类模型的值。

所有差值均大于0，表明基线时间序列存在白噪声和有色噪声，该结果与谱指数计算结果完全吻合。

3.3 噪声强度分析

利用极大似然估计法算出每条基线在3类噪声模型下的极大似然估计，并计算出其在WN+ FN+RWN模型下的噪声强度，每条基线3维分量的噪声强度如表2所示。

表2 3维分量噪声强度值

由表2可以得出：在方向上URUM—WUHN基线与其他基线相比具有独特的噪声特性，将其剔除后进行研究；在方向上，当基线长度小于2500 km时，时间序列中主要表现为WN和FN 2种噪声，当基线长度大于2500 km时，存在WN、FN和RWN 3种噪声；在方向上，时间序列中主要包含WN和RWN 2种噪声；在方向上，主要存在WN和FN 2种噪声。

利用WN+FN+RWN噪声模型下的噪声强度分别求出WN、FN、RWN占据总噪声成分下的比例。例如，在方向WN的各个基线总噪声强度为37.71，其中3种噪声的总强度为99.98，所以在方向上WN占总噪声的37.72%。其他噪声含量值求得过程与此类似。

4 结束语

在阐述谱指数法和极大似然估计法原理的基础上，选取中国大陆6个IGS站组建了不同长度的长基线，采用周期图估计法求出每条基线、和分量的谱指数以确定噪声成分，并利用极大似然估计法对噪声进行分析，得出最优噪声模型。最后得到如下结论：

1）建立了基线长度与最优噪声模型之间的关系，且、和具有不同的噪声特性。在方向上，当基线长度大于2500 km时，最优噪声模型为WN+FN+RWN，而当基线长度小于2500 km时，WN+FN为最优噪声模型；在方向上，最优噪声模型是WN+RWN；在方向上，最优噪声模型是WN+FN。

2）定性了噪声种类，量化了其所占比重。基线时间序列包括白噪声和有色噪声。在方向上，当基线长度大于2500 km时，WN占10.05 %，FN占46.86 %，RWN占43.09 %，而当基线长度小于2500 km时，WN占18.99 %，FN占78.86 %；在方向上，WN占37.72 %，RWN占62.22 %；在方向上，WN占9.67 %，FN占89.88 %。

鉴于URUM—WUHN基线同时具有WN+FN+ RWN 3种噪声特性，与本文得出的规律不符，可能与测站的地质结构有关，后期将对其做深入研究。

[1] 李昭, 姜卫平, 刘鸿飞, 等.中国区域IGS基准站坐标时间序列噪声模型建立与分析[J].测绘学报, 2012, 41(4): 496-503.

[2] 姜卫平, 李昭, 刘鸿飞, 等.中国区域IGS基准站坐标时间序列非线性变化的成因分析[J].地球物理学报, 2013, 56(7): 2228-2237.

[3] 黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学, 2006，26(2): 31-38.

[4] 黄立人, 符养. GPS连续观测站的噪声分析[J].地震学报, 2007, 29(2): 197-202.

[5] MAO A, HARRISON C G A, DIXON T H. Noise in GPS coordinate time series[J]. Journal of Geophysical Research Atmospheres, 1999, 104(B2): 2797-2816.

[6] 姜卫平, 周晓慧.澳大利亚GPS坐标时间序列跨度对噪声模型建立的影响分析[J].中国科学:地球科学, 2014, 44(11): 2461-2478.

[7] 张恒璟.国家CORS基准站高程时间序列非线性时变研究[D].阜新: 辽宁工程技术大学, 2013.

[8] 张风霜,武艳强, 孙东颖. 中国大陆GPS连续观测站基线时间序列分析[J].地震, 2011, 31(4): 86-97.

[9] 徐克科, 李伟.利用GNSS基线分析芦山Ms7. 0级地震前后应变演变特征[J].武汉大学学报(信息科学版), 2017, 42(8): 1054-1060.

[10] WANG K, JIANG W, CHEN H, et al. Analysis of seasonal signal in GPS short-baseline time series[EB/OL]. [2018-10-28].https://www. researchgate. net/publication/324707621_Analysis_of_Seasonal_Signal_in_GPS_Short-Baseline_Time_Series.

[11] 刘宗强, 党亚民, 杨强,等. 顾及共模误差的四川连续GPS基准站坐标时间序列噪声分析[J].大地测量与地球动力学, 2018, 38(5): 510-515.

[12] MANDELBROT B, NESS J. Fractional Brownian motions, fractional noises and applications[J]. Siam Rev, 1968, 10(4)：422-439.

[13] ZHENG W, WANG Z, DING Y, et al. Accurate establishment of error models for satellite gravity gradiometry recovery and requirements analysis for the future GOCE Follow-On mission[J]. Acta Geophysica, 2016, 64(3)：732–754.

[14] LANGBEIN J. Noise in GPS displacement measurements from southern California and southern Nevada[J]. Journal of Geo-physical Research: Solid Earth, 2008, 113(B5)：620-628.

[15] WILLIAM S D P, WILLIS P. Error analysis of weekly station coordinate in the DORIS network[J]. Journal of Geodesy, 2006, 80(8-11)：525-539.

[16] 叶锦强. 基于CATS软件的GPS时间序列分析[J].地理空间信息, 2015, 13(6): 121-123，126.

[17] LANGBEIN J. Noise in two-color electronic distance meter measurements revisited[EB/OL]. [2018-10-28]. https: // agupubs. onlinelibrary. wiley. com/doi/10. 1029/2003JB002819.

Baseline time series noise analysis of IGS reference stations in Chinese mainland

JI Changdong, SHEN Yifan, WANG Qiang

（Liaoning Techical University, Fuxin, Liaoning 123000, China）

Aiming at the problem that it is difficult to separate the signal from the noise in baseline time series, the paper proposed a method of determining the optimal noise model: power law model (PLM) was combined with maximum likelihood estimate (MLE) to derive the power spectral index of three-dimensional coordinate vectors and the maximum likelihood estimation, and the optimal noise model was given; then the observation data of 6 years from 6 IGS stations in Chinese mainland was taken as the example to verify the feasibility of the method. Experimental result showed that there would exist white noise (WN), flicker noise (FN) and random walk noise (RWN) in the baseline time series;in thedirection, when the baseline length is between 1015~2500 km, it would be shown as WN+FN, and when the length is longer than 2500 km and shorter than 3225 km, it would be shown as WN+FN+RWN, with RWN accounting for 43.09 %; in theanddirections, the optimal noise models would be WN+RWN and WN+FN respectively, with RWN accounting for 62.11 % and FN for 89.88 %.

global navigation satellite system (GNSS); International GNSS Service (IGS) reference station; time series of baseline; spectral index; maximum likelihood estimation; noise model

吉长东，沈祎凡，王强.中国大陆IGS基准站基线时间序列噪声分析[J].导航定位学报,2019,7(3):108-114.（JI Changdong，SHEN Yifan，WANG Qiang.Baseline time series noise analysis of IGS reference stations in Chinese mainland[J].Journal of Navigation and Positioning,2019,7(3):108-114.）

10.16547/j.cnki.10-1096.20190318.

P228

A

2095-4999(2019)03-0108-07