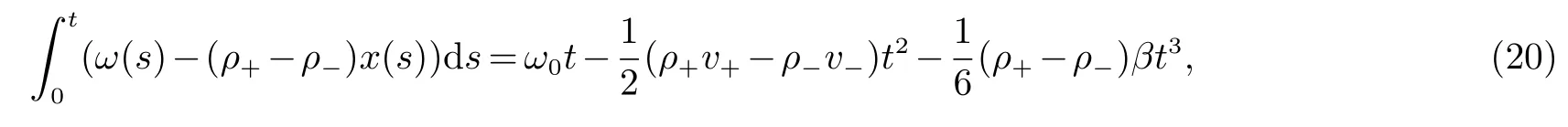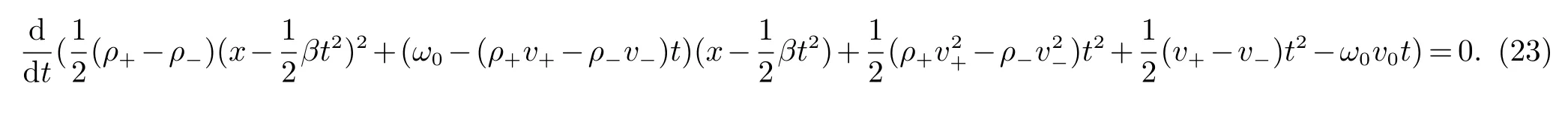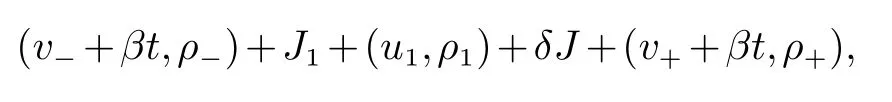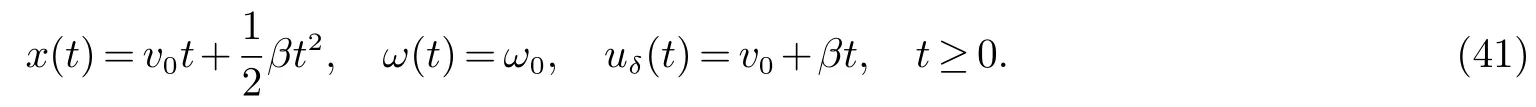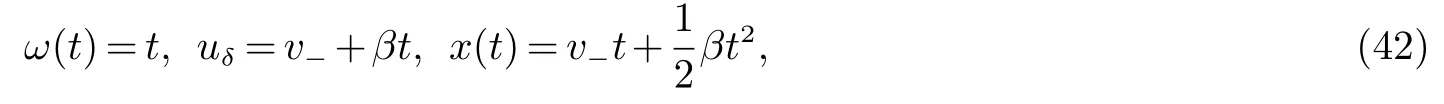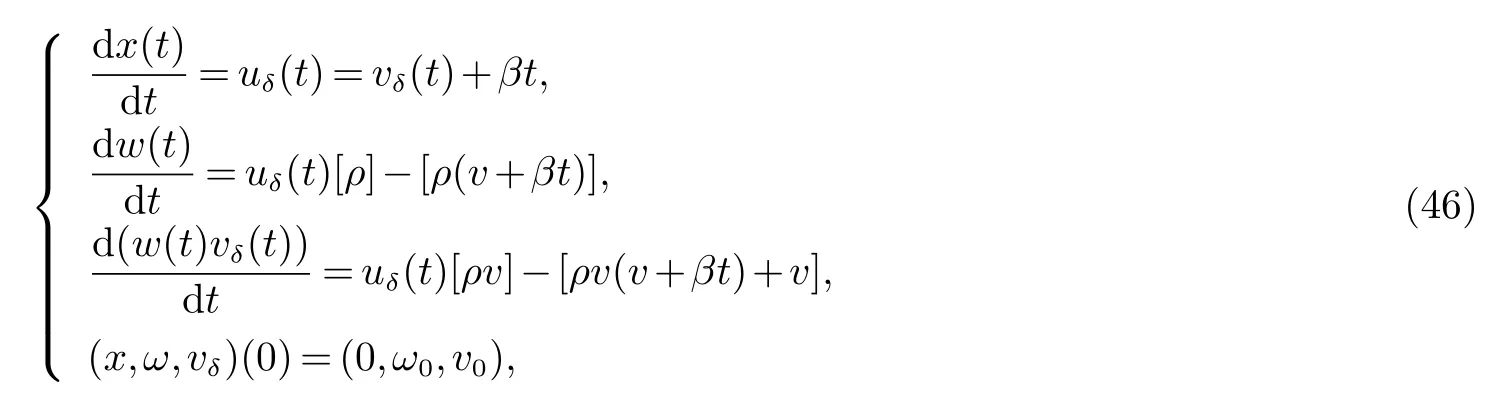带有源项的Chaplygin气体非对称Keyfitz-Kranzer方程组含狄拉克初值的广义黎曼问题∗
宋赟,郭俐辉
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
带有源项的Chaplygin气体非对称Keyfitz-Kranzer方程组具有以下形式

其中β是常数,ρ(x,t),u(x,t)分别表示密度和速度,压力P满足

当β=0时,方程组(1)属于非对称Keyfitz-Kranzer方程[1]

其中φ(ρ,u)=f(u)−P(ρ).方程组(1)是由Aw和Rascle[2]提出的关于交通流的宏观模型,其中压力P是光滑的、严格递增函数且满足

关于Aw-Rascle模型的更多结果,读者可参看[3-5].Lu[6]对方程组(1)作如下假设


称为带有源项的Chaplygin气体非对称Keyfitz-Kranzer方程组含狄拉克初值的广义黎曼问题,其中ω0>0,ρ±>0,u±,u0是常数.关于狄拉克初值的广义黎曼问题,读者可参看[11-14].Li[15]利用速度变换

得到了方程组(1)–(2)的黎曼解,其中速度变换(5)是由Faccanoni和Mangeney[16]提出的.
本文主要研究了初值问题(1)–(2)和(4)的解.方程组(1)–(2)的所有特征都是线性退化的,故其基本波为接触间断.当时,其黎曼解中会出现狄拉克激波.在一些宇宙学理论中,狄拉克激波的形成表明了宇宙在不同时期的进化.关于狄拉克激波的研究,请参看[17-24].
1 预备知识
在本节中,我们简单陈述方程组(1)–(2)的黎曼问题,关于此问题的详细理论读者请参看[15].
运用速度变换(5),方程组(1)–(2)可以转化为守恒律形式

由[15]可知,相平面可分为五个区域(见图1).

图1 (ρ,v)-平面Fig 1 Phase Plane
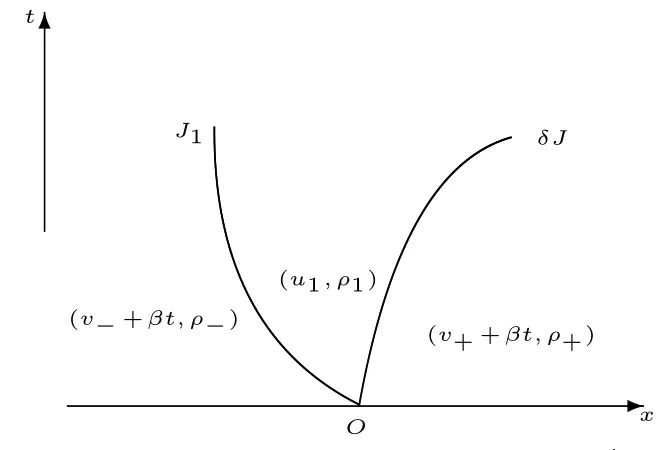
当右状态 (v+,ρ+)∈(I∪II∪III∪IV)时,解由接触间断J1和J2组成,且

中间状态 (v∗,ρ∗) 满足

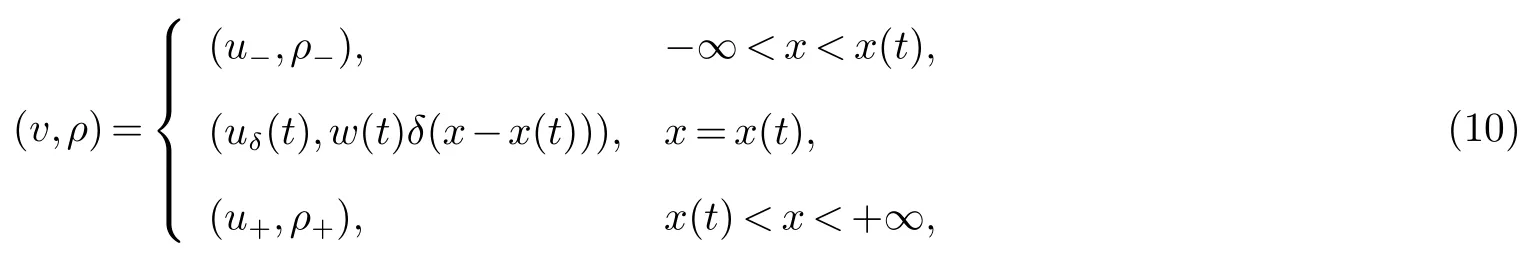
w(t)和uδ(t)=vδ+βt分别表示狄拉克激波的权和速度,且狄拉克激波满足下面的广义Rankine-Hugoniot条件

由(11)式,可得:
当 ρ+6=ρ−时,

当 ρ+=ρ−时,

且狄拉克激波满足如下形式的广义熵条件

此外,广义Rankine-Hugoniot条件(11)式也等价于广义Rankine-Hugoniot条件
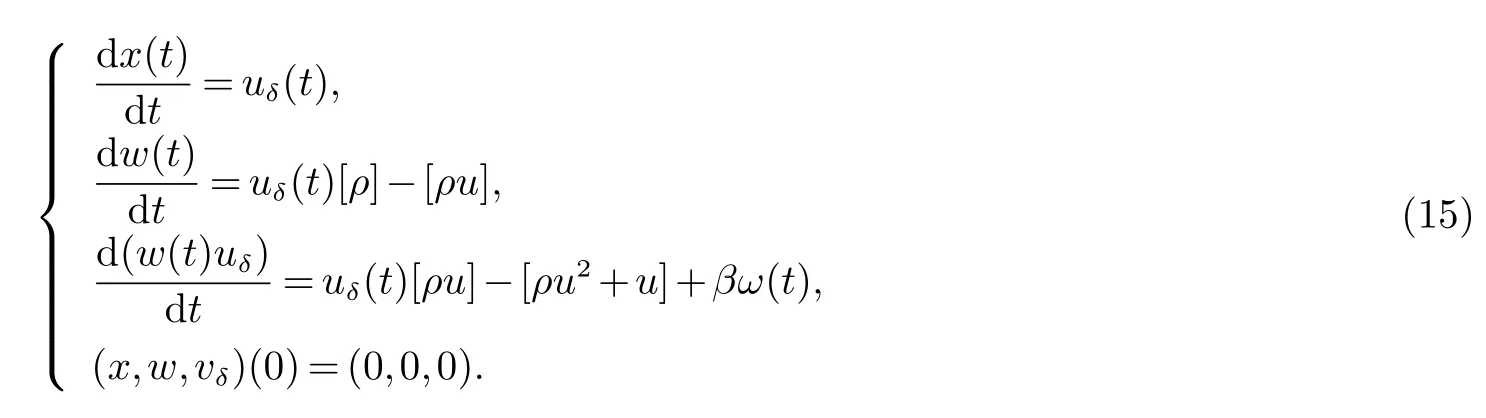
2 带有狄拉克初值的黎曼问题
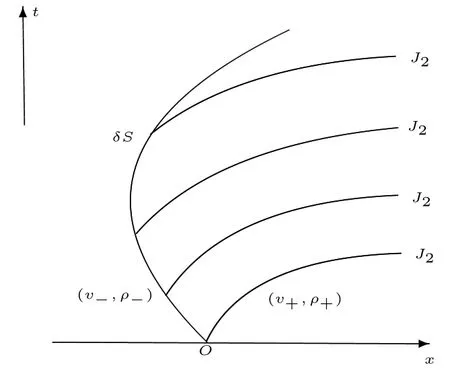
情形1

图2 情形1:v+++ 且狄拉克激波解(16)满足如下广义Rankine-Hugoniot条件 其中[ρ]=ρ+−ρ−. 接下来,通过求解常微分方程(17)式,我们可得到狄拉克激波的位置、权和速度. 对(17)式两边从0到t积分,可得 由(18)式得 从而(19)式可化为 (22)式等价于 对(23)式在[0,t]上积分,可得 当ρ+6=ρ−时,我们有 由(18)式和(24)式,可得 其中 由v++ 当ρ+=ρ−时,(24)式是关于变量x的一个线性函数,因此 从(18)式,可得 由(30)式和(21)式,可得 注1(渐近性) 当 ρ+6=ρ−时,由(25)–(28)式,我们有 和 (32)–(34)式与初值问题(1)–(2)的黎曼解中狄拉克激波的权、位置和速度相同.类似,当ρ+=ρ−时,可得到相同的结果.这表明在初值(4)下构造的黎曼解是稳定的. 注2当v0=0,ω0=0,初值问题(1)–(2)和(4)的黎曼解与方程组(1)–(2)的黎曼解相同. 情形2v−≤v0≤v++. 根据 v0,v−,v++的大小关系,又可以分四种子情形进行讨论. 情形2.1v− 当t充分小时,初值问题(1)–(2)和(4)的解可构造为(见图3) 图3 情形2.1:v− 其中 狄拉克激波满足广义Rankine-Hugoniot条件(17),其中[ρ]=ρ2−ρ1.当把(25)–(28)式中的−,+分别换成1,2时,我们可得狄拉克激波的速度、位置和权分别为 当ω(t)=ω0−t=0时,有t1:=t=ω0,这表明δ-激波在t1时刻消失(见图3). 当t>t1时,我们可构造如下形式的解(见图3) 其中 接触间断J1,J2的传播速度分别为 情形2.2v−=v0 我们构造初值问题(1)–(2)和(4)的解为(见图4) 图4 情形2.2:v−=v0 图5 情形2.3:v− 其中u2,ρ2由(35)式给出,接触间断J2的传播速度由(39)式给出.狄拉克接触间断的速度、位置和权分别为 我们可验证狄拉克接触间断满足广义Rankine-Hugoniot条件(17). 情形2.3v− 与情形2.2类似,初值问题(1)–(2)和(4)的解可构造为(见图5) 狄拉克接触间断的位置、权和速度分别为 情形2.4v−=v0=v++. 初值问题(1)–(2)和(4)的解为 其中狄拉克激波的权、速度和位置分别为 易验证(42)式满足广义Rankine-Hugoniot条件(11).此外,狄拉克激波满足熵条件 注3当v0=0,ω0=0时,则初值问题(1)–(2)和(4)的黎曼解与方程组(1)–(2)的黎曼解相同. 情形3v0 我们寻找初值问题(1)–(2)和(4)的具有如下形式的分片光滑解(见图6) 图6 情形3:v0 狄拉克激波满足广义Rankine-Hugoniot条件 其中 [ρ]=ρ∗−ρ−. 由式(45)和(46)2,可得 联立(45)式及(46)3,我们有 根据(47)–(48)式,我们得到与[13]一致的等式 其中 A=ω0(ρ−v−+1−ρ−v0),并且 令 可得 从而由(49)式和(51)式,得到狄拉克激波的权为 进而,有 这表明δ–激波永远不会穿过J2. 当v− 情形4v0 在这种情形下,由(55)式,可知存在唯一的t∗,使得uδ(t∗)=v+++βt(见图7).因此,当 0≤t≤t∗时,初值问题(1)–(2)和(4)的解与情形3相同 图7 情形4:v0 其中,当0 当 t>t∗时,假设 t=t∗∗时,δS1将全部穿透 J2.当 t∗ 其中 [ρ]=ρ∗(t1)−ρ−. 当t>t∗∗时,解的表达式与情形1类似.可以构造如下形式的解(见图7) 这里,t∗∗由决定.其中,位置、权和速度满足广义Rankine-Hugoniot条件 (17)和初始条件 下面,我们给出主要结果. 定理1初值问题(1)–(2)和(4)的解有如下情形: (1)当v++ (2)当v−≤v0≤v++时,(1)–(2)和(4)的解中包含接触间断,狄拉克激波和狄拉克接触间断. (3)当v0