基于大数据技术的电能计量器具质量评估及优选方案∗
罗 庆,张新燕,罗 晨,李 江,晁 勤
(1.新疆大学电气工程学院,新疆乌鲁木齐830047;2.国网新疆电力公司电力科学研究院,新疆乌鲁木齐830011;3.国网新疆电力公司昌吉供电公司,新疆昌吉831100)
0 引言
电能计量器具应用广泛,器具的质量问题关系到广大人民群众的切身利益.如今电子式电能计量器具应用广泛,计量精度不断提高,但也带来了新的问题.尽管现在对器具的质量检测工序已经较为成熟,但由于电能计量器具的应用数据量十分庞大,验证整体质量的检测样本方法明显不足,缺乏可靠的技术数据支撑.
学者提出了多种检测电能计量器具质量问题的方法,如文献[1-3]阐述了谐波对电能表计量性能的影响及其原因,以及在谐波情况下电能计量的校正方法;文献[4]提出了电能器具增加硬件处理谐波,改进电能计量性能的方法;文献[5-6]对电能计量装置的内部结构进行拆解,分析各部分元件的运行误差并以此评价装置的误差特性.上述研究方法对电能计量器具性能提高和质量检测有很大作用,但对庞大数量的器具仅采用少量样本检测,仍不能充分验证整体质量的优劣.
随着大数据技术不断的发展与应用,可实现海量数据的分析挖掘处理,因此本文提出能够全面有效的解决电能计量器具整体质量评估及优选的方案:把大数据技术应用在电能计量设备中,利用已经记录、检测、维修等产生的产品数据,建立详细的大数据库,在庞大的样本中应用新的方法计算计量器具的二次良品率、故障负效益比、优劣误差预值分布率等性能指标,并进行质量分析;同时对电能计量器具性能指标采用多变量因子加权方法构建质量评估模型;根据用户对电能计量器具使用年限、故障维修费用、计量准确度等不同需求为目标,确定不同的加权因子权值和阈值范围,计算获得最佳质量评估值,为用户提供电能计量器具生产厂家的合适选择方案,并给出电能计量器具的整体性能优劣、使用年限长短等定量指标.
1 构建电能计量器具质量评估与优选方案的技术路线
电能计量器具应用广泛,其质量的优劣关系到用户的切身利益,国家、行业乃至地方均对电能计量器具制定了相关的标准要求[7−10].物联网时代,网络技术已将相关电能计量器具进行了智能联网,可对电能计量器具的性能检测、日常维护数据进行记录,按照相关标准和规定对其进行检测和维护,计量精度越高,检测和维护频率越大,相关记录的数据也越详细,从而可以组建电能计量器具的大数据库[11−13].利用大数据技术,采用统计方法区别各厂家电能计量器具的二次良品率、优劣误差预值分布率、故障负效益比等性能指标,将分析计算的性能指标进行多变量因子加权,构建电能器具的质量评估模型,结合用户给出的约束条件,确定计量器具的优选方案供用户选择优质的产品,其流程如图1所示.

图1 基于大数据的电能计量器具质量评估与优选方案流程图Fig 1 Based on large data of the energy measurement equipment quality assessment and optimization program flow chart
1.1 电能计量大数据的构建
大数据是指大量的、结构复杂的、更新速度快的实际数据[8].电能计量器具的种类是多样的,日常需求量庞大.电能计量器具在不断更新,按照相关标准及规定对器具进行周期性检测、日常维护能够产生足够多的数据[14−16].因此,建立电能计量大数据系统是可行的.
电能计量大数据系统基于产品的各类信息构建.主要信息有产品的类型、出厂编号、生产日期、准确级别、使用记录、维护记录、误差记录等,对这些数据进行详细地统计记录,可以构建电能计量大数据系统,如图1所示.
1.2 电能计量器具质量评估与优选方案
根据电能计量器具的相关标准及规定,对大数据中相关质量性能检测数据分析、统计计算,得到二次良品率、优劣误差预值分布率、故障负效益比等性能指标,对各相关指标进行权重分配,构建质量评估模型.
在建立的质量评估模型基础上,以满足用户需求的效益最大化确定加权因子,给出优选方案供用户参考选择,具体流程如图2所示.

图2 电能计量器具质量评估与优选方案示意图Fig 2 Survey on quality evaluation and optimization scheme of energy metering apparatus
2 质量指标及评估模型构建与优选方法
2.1 电能计量器具二次良品率计算方法
电能计量器具出厂检验有严格的检定规程和标准,产品出厂必须达到一定的良品率,但在器具出厂后,随着使用时间的推移,电能计量器具会出现各种问题.由此,设定电能计量器具的二次良品率是合格出厂的器具在使用期间内设备的完好率,即

xt为二次良品率,t为出厂至使用的时间,m为正常使用的良品,N为开始购买同一批使用的电能计量器具数.用户可根据使用年限、二次良品率的高低决定采购相应器具,如四年使用的二次良品率、八年使用的二次良品率等.
2.2 电能计量器具故障负效益比计算方法
将电能计量器具的故障类型进行分别统计,由于故障类型的不同,器具的维修难度及费用多少不同,定义故障负效益比计算方法如下

其中:yt为在t时间内,电能计量器具的故障负效益比;i为故障类别;ni为i故障下的电能计量器具数目;Pj为i故障下的维修费用;N为购买同一批开始使用的电能计量器具;P为购买价格.
2.3 电能计量器具误差优质率计算
电能计量器具准确度一般可分为0.01级、0.02级、0.2S级、0.5S级、1级、2级等,根据精确度可得出规定误差范围,如a等级,则其误差范围为[-a,a].将a等级下的电能计量器具误差范围进行划分,如(3)式

将t年检测误差数值落入各区间的数据进行统计,得到误差优质率,如(4)式

Zt为在t年内产品误差优质率;m为在t年内,m个器具的误差在(−K,K)最优区间内;N为整体使用的器具数.
2.4 基于加权因子的质量评估模型构建
根据计算计量器具的二次良品率、优劣误差预值分布率、故障负效益比等性能指标,将各性能指标进行加权因子,构建质量评估模型如下

其中α+β+γ+...=1,α,β,γ...∈(0,1),为各质量指标的加权因子;i为电能计量器具的生产厂家.
2.5 基于需求响应的优选方案
计量器具种类繁多,用户需求往往是多方面的,优选方案是根据用户的需求确定最优计量器具.在建立(1)式的质量评估模型基础上,按照用户多目标需求,利用用户对电能计量器具良好使用年限、故障维修费用、计量准确度等不同需求为目标,确定不同的加权因子权值和阈值范围,计算获得最佳质量评估值,为用户提供合适的电能计量器具生产厂家选择方案.具体方法:如果良好使用年限、故障维修费用、计量准确度需求一样,α+β+γ+...=1平均分配确定权值;如果良好使用年限、故障维修费用、计量准确度需求不一样,有侧重点,α+β+γ+...=1不能平均分配确定权值,需要给出阈值范围,如侧重二次良品率,最小权值0.5,最大权值0.6,其余两个平均分配各0.2或0.25,如果两个均侧重,则用0.4、0.4、0.2分配,由此给出需求响应的优选方案,供用户参考选择.
3 实例分析与方法验证
应用大数据技术对某地区检测中心的高精度标准电能表构建2009年至2016年8年内检测到的大数据样本,样本见表1所示.
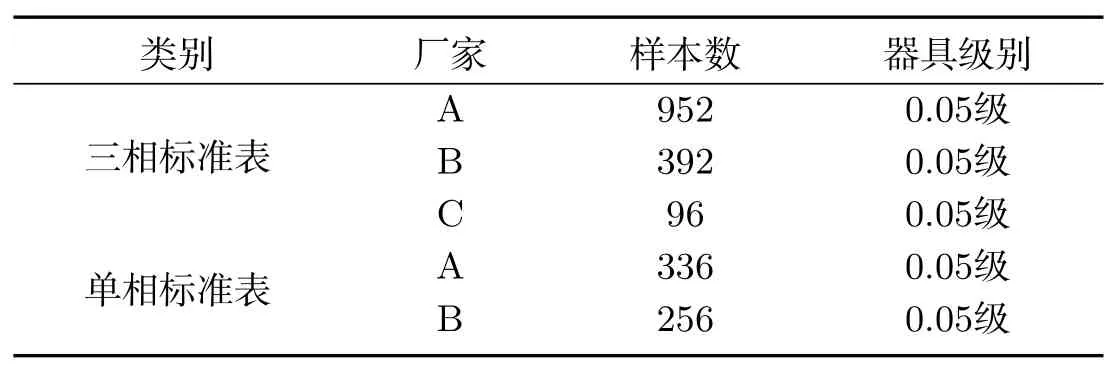
表1 某地区8年标准样本数据表Tab 1 8 years in the area standard meter data
根据样品8年的检测数据,对器具的二次良品率、故障负效益比、误差情况分析计算.
3.1 二次良品率计算验证
按照式(1),将8年样品分为1∼4年和5∼8年两个均等时间段,计算各厂家样品的二次样品率,结果如表2所示.

表2 某地区标准表二次良品率统计Tab 2 The area of the second grade of the standard table
从表2中的数据可以得到:
(1)对比使用时间在1∼4年之间的三相标准表数据,A厂的二次良品率较B厂高出1.44%,但其单相标准表在此期间内的二次良品率低于B厂1.14%;
(2)对比使用时间在5∼8年之间的三相标准表数据,A厂三相标准表的良品率较C厂高出1.12%.
由以上分析得出结论,A厂家三相标准电能表的二次良品率较高;B厂家单相标准电能表二次良品率较高.并且随着器具使用时间的增长,二次良品率均呈现下降趋势.
3.2 器具故障负效益比计算验证
依据国标1805-2013对三相标准电能表进行检定,统计器具的故障数,根据各类实际维修产生的费用,按照公式(2)计算故障负效益比,结果如表3所示.

表3 某地区三相标准表故障统计Tab 3 Standard in the area of three-phase fault statistics table
从表3中可以看出使用时间在1∼4年之间的三相标准表,负效益比较优的为B厂;在5∼8年之间的三相标准表,负效益较优的为A厂.
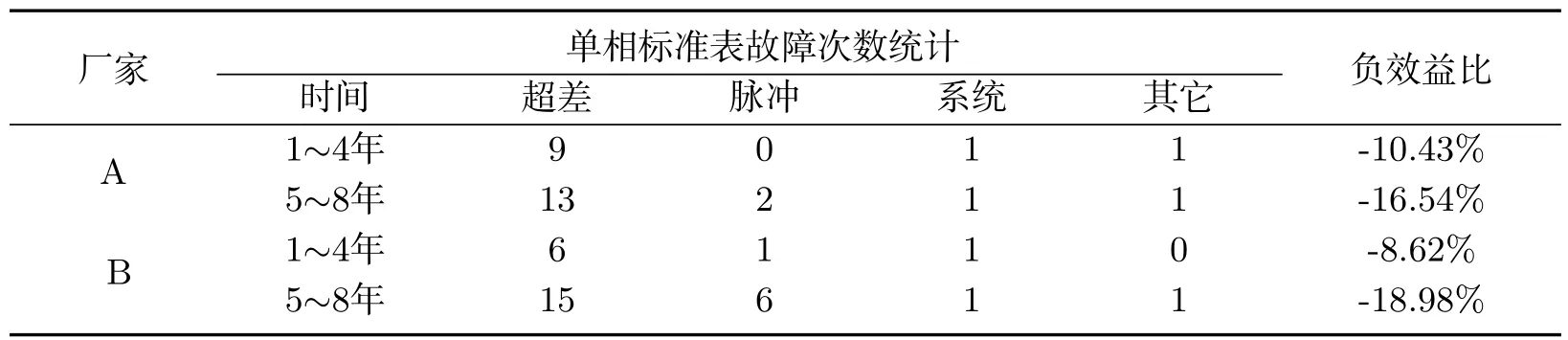
表4 某地区单相标准表故障统计Tab 4 In the area of single-phase standard fault statistics
在表4中可知使用时间在1∼4年的单相标准表,负效益较优的为B厂;在5∼8年之间的单相标准表,负效益较优的为A厂.
3.3 器具误差预值优质率计算验证
标准表检定中最关键的项目是电能误差检测,标准表的误差准确度关系到其检验的电能计量器具的合格性及稳定性.标准电能表样品准确度为0.05级,按公式(3)(4)将误差区间[-0.05,+0.05]进行划分,K=5,定义区间一[-0.01,+0.01]为优品,区间二[-0.03,-0.01)∪(+0.01,+0.03]为良品,区间三[-0.05,-0.03)∪(+0.03,+0.05]为中品,统计检测各样品误差时间段内在各区间的分布情况,如表5所示.
将各厂家的优质率绘成矩形图对比,如图3所示.
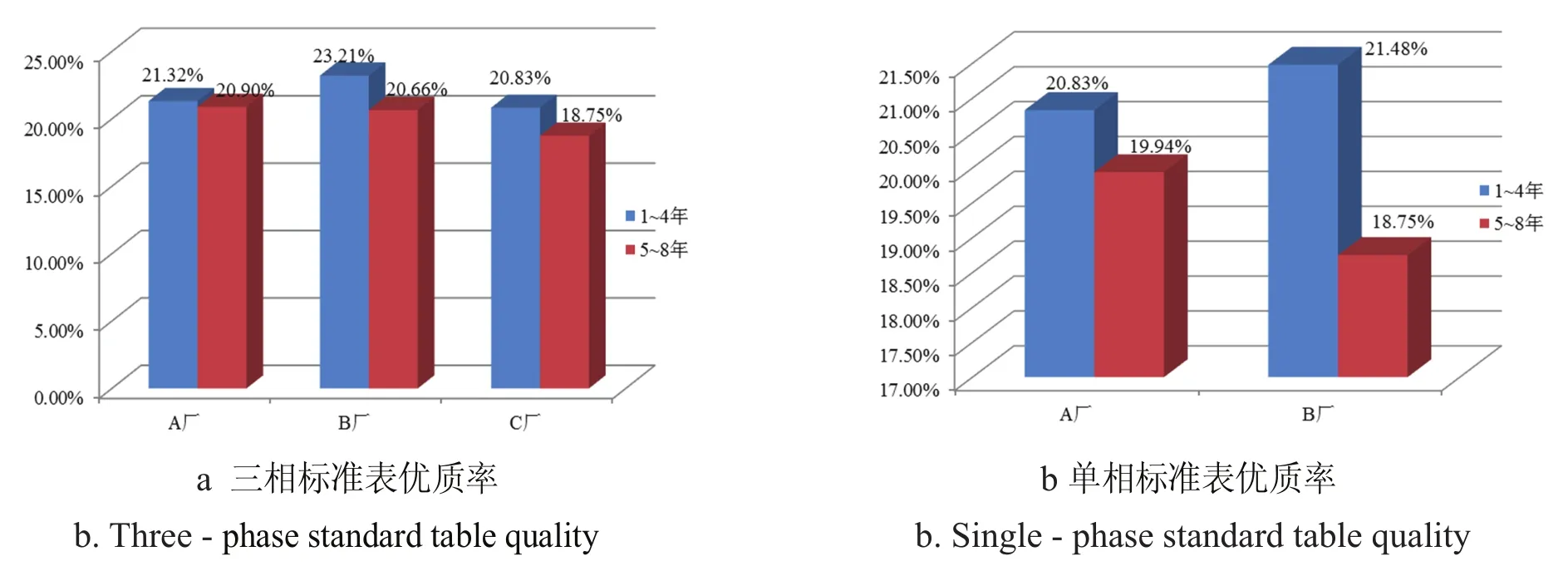
图3 单、三相标准电能表时间段上的优质率Fig 3 Single,three-phase standard energy meter on the time rate of high quality

表5 三相标准电能表优、良、中等级统计Tab 5 The standard power table excellent,good,medium level statistics
由图3a可知在1∼4年内,B厂家三相标准电能表优质率最高,但在5∼8年中A厂家最高,且A厂家优质率变化较小,B厂家优质率变化最大;由图3b可知在1∼4年内,B厂家单相标准电能表优质率最高,但在5∼8年中A厂家最高,且A厂家优质率变化较小,B厂家优质率变化最大.
3.4 器具质量评估与优选方案
根据上述算例中各时间段检测质量性能指标值,按照用户需求对加权因子进行固化,代入公式(5),以此确定各厂家计量器具的优选方案.如用户需求在1∼4年和5∼8年均要求少维护、良品率高的单、三相标准电能表,选择0.333权值均分计算出三相标准电能表A、B、C三家1∼4年fi(α,β,γ)max分别为37.17%、37.97%、37.38%;5∼8年分别为35.51%、33.82%、30.80%;单相标准电能表A、B二家1∼4年fi(α,β,γ)max分别为35.47%、36.67%;5∼8年分别为32.55%、32.05%;由此可知,用户在1∼4年时间段内,最优计量器具应为B厂家的单、三相标准电能表;如用户在5∼8年时间段内,最优计量器具分别为B厂家的单相标准电能表,A厂家的三相标准电能表.
综上所述,在大数据技术支撑下,针对三个厂家的三相标准表,给用户详实的技术报告,并提供质量评估模型,在用户需求响应下提供优选方案,让用户选择合适的计量器具.
4 结论
文章分析了电能计量大数据系统的可行性,首次提出计量器具的二次良品率、优劣误差预值分布率、故障负效益比等性能指标的计算方法,并构建了质量评估模型和供用户选择的优选方案;应用具体的标准电能表计量数据进行实例分析,证明了大数据系统在电能计量工作中的实用性.可得出以下结论:
(1)电能计量大数据系统的建立,可以对厂家产品进行详细准确的技术分析,促进其产品更新.
(2)电能计量大数据系统的应用,有助于选择更加合适的产品以满足用户需求.
(3)电能计量产品的各项性能参数的计算,有助于电能计量产业的良性循环发展.
本文在对方案进行决策时,未考虑各项检测质量指标的相关特性及耦合性,对质量指标相互影响因子分析不深入,对计量器具的质量评估不够精细,将在后续的研究中予以完善.

