双有源桥DC/DC变换器的三移相优化控制∗

张瑶，程志江，陈星志

(新疆大学电气工程学院，新疆乌鲁木齐830047)

0 引言

目前，全球为了应对能源与环境问题，具有可再生特性的风、光等新能源在电力系统中的接入比例日益增加[1,2]，可再生能源发电系统和分布式储能系统在接入大电网的过程中，需要使用隔离式DC/DC转换器实现能量传输[3,4]．由于双有源桥（Double Active Bridge，DAB）DC/DC变换器具有能量双向传输、功率密度高、易于实现软切换、无需任何额外的无源元件等优点[5,6]，因此常用于微电网系统．隔离式双有源桥DC/DC变换器在单向DC/DC变换器的基础上将一端的整流桥替换为和另一端结构相同的全桥，变压器采用高频变压器．在DAB中，变压器的漏电感作为能量传递元件，功率通过绕组电压之间的移相比来调节．

传统DAB调制策略为单移相控制[7−10]，单移相控制只控制一二次全桥之间的外移相比，不考虑一二次全桥各自的内移相比，因此只有一个自由度，相比较于三移相控制，单移相控制方式简单并且易于实现．但是单移相控制在一二次侧直流母线电压不同时或轻载情况下无法实现开关管的零电压软开关，造成开关损耗，对于电路中产生的回流功率无法消除，并且开关管的电流应力较大，从而导致变换器效率降低，所以单移相控制具有很大的局限性．为了克服单移相控制的局限性，文献[11]提出双移相优化控制来减小电感电流应力，但是双移相控制是三移相控制一二次侧全桥两个内移相比相等的特殊形式，所以双移相控制的最优解只是局部最优解．文献[12,13]提出三移相控制，分析出减小开关管导通损耗的条件，但是没有涉及到全功率范围内减小电感电流有效值．

本文主要针对三移相控制展开研究，首先在忽略DAB变换器中励磁电感的条件下简化DAB变换器的电路模型，得到DAB的等效电路，将一二次侧三电平交流输出电压分解为几个标准方波的和，将电感电流分解为几个标准三角波的和，并求出电感电流有效值以及传输功率表达式．接着依据三移相控制三个移相比之间的关系，分为六种工作模式，并指出仅有三种工作模式是有效工作模式．然后根据电感电流有效值最小和提高传输功率的目标建立优化方程，在三种有效模式下分别求优化方程的解，得出高中低功率下的最优控制参数．最后通过仿真结果验证了此三移相优化控制方法是可行的．

1 DC/DC变换器的三移相控制

1.1 DAB拓扑结构

图1是三移相控制DAB的拓扑结构，在稳定状态期间，DAB相当于连接在电感两侧的两个高频交流电源[14]．此时是DAB的无损电路结构，假设变压器的磁化均方根电流Im可忽略不计（其中Im指的是一次侧端口），此外，也忽略电流谐波引起的额外高频损耗的影响，这两个条件对于磁变压器磁芯来说是假设的，这两种假设常用于DAB变换器的研究．

图1 DAB变换器拓扑结构Fig 1 Topology of the DAB converter

其中，L是高频变压器的串联电感和漏电感之和，Sx表示半导体开关，它由有源开关Tx和反并联二极管Dx组成，Cx是结电容，N是变压器一次侧到二次侧的匝数比，V1和V2分别是一次侧全桥和二次侧全桥两端的直流输入电压，电压转换比M定义为NV1/V2，Vab和Vcd分别是一次侧全桥和二次侧全桥两端的交流输出电压；iL是电感电流，其中二次侧全桥端输入电压转换到一次侧全桥的等效交流输出电压Vab=NVcd．

1.2 三移相控制开关时序

各个开关管导通时序以及一二次侧电压电流如图2所示，Vab和Vcd作为三电平交流电压工作，在本文中每个信号保持半开关周期，开关管T1的开通初始时间定义为零时间．D1和D2分别是一次侧全桥和二次侧全桥的内移相比．D3是Vab和Vcd之间的外移相比．三个移相比的范围是0≤D1≤1，0≤D2≤1，并且-1≤D3≤1，其中正D3表示T1的超前于T5导通，功率正向流动，负D3表示T5超前于T1导通，功率反向流动，T是开关周期．在功率正方向传输时，在分析中忽略外移相D3大于0.5的值，因为外移相D3在大于0.5小于1时会导致变换器中电流增大，因此D3被限制在0至0.5之间，同理当功率传递方向相反时，D3应被限制在-0.5至0之间．因此，D3在区间[-1/2，1/2]范围内，它可以实现全传输功率和更好的性能．

图2 三移相控制开关时序图Fig 2 Switching timing diagram of triple phase shift control

1.3 电压电流功率分析

根据图2两个桥臂的驱动信号可知Vab为一次侧全桥通过移相比D1产生的三电平方波，Vcd为二次侧全桥通过移相比D2产生的三电平方波，这两个通过移相产生的三电平方波可以分解为两个方波之和的形式．

图3 三电平方波的合成Fig 3 Synthesis of a three level square wave

图4 双有源桥变换器的等效电路图Fig 4 Equivalent circuit diagram of a dual active bridge converter

如图3所示，S(t)表示幅值为0.5，周期为2T的标准两电平方波，S(t−DT)则表示比S(t)方波滞后了DT时间的方波．S(t)与S(t−DT)就可以叠加为幅值等于1，占空比等于1−D，周期等于2T的三电平方波．所以，Vab和Vcd可表示为：

V1为变换器的输入端直流电压，V2表示变换器的输出端直流电压．因此，双有源桥变换器的电路图可等效为图4结构．

根据图4的等效电路可得出电感电流的微分方程为

得出

Tr(t)表示S(t)的积分函数，是一个对称的三角波，所以双有源桥中的电感电流值实际上是由四个三角波形叠加而成的．因此可以得出变换器传输功率为

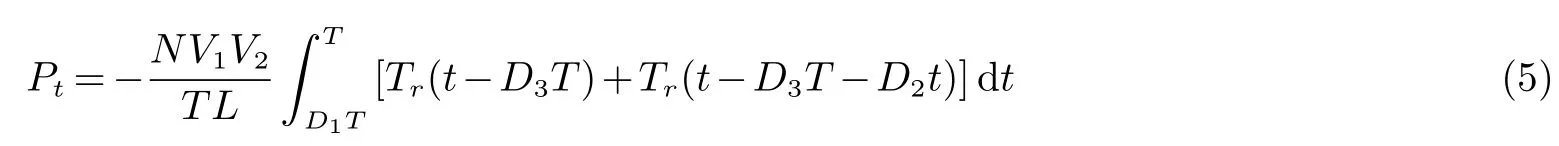
电感电流有效值的平方值为

1.4 三移相控制的六种工作模式

根据两侧全桥的切换顺序区分基本切换模式．为便于表示V1端口到V2端口的电源传输定义为“充电”，反向操作定义为“放电”．因为Tr(t)是分段函数，所以对于不同工作模式有不同的表达式，考虑到变换器的工作波形，根据D1，D2和D3之间的范围分别有六种可能的工作模式，各工作模式下三个移相比的关系如表1所示．

表1 各工作模式的三个移相比关系Tab 1 Comparison of three shifts of each working mode

图5 六种开关模式的工作波形Fig 5 Operating waveforms in six switch modes

图5是充电情况下的不同工作模式的等效电路和工作波形．由于功率传输的方向仅由D3确定，充电情况及其相应的放电情况拥有相同的内部相移比，但是D3相反．因此D3>0时充电，D3<0时放电．因此，对充电情况的分析足够充分，对于相应的放电情况可以得到相同的结论．可以从图5中获得描述切换模式的当前波形的表达式，然后可以导出每个切换模式的传输功率和电感电流．

由图5可以看出工作模式2、3、6，没有Vab·Vcd>0的时间段，就说明能量不能直接从转换器的输入端口向输出端口传递，应先将能量储存在电感中，再通过电感将存储的能量传递到输出端，这三种工作模式会造成额外的回流功率，而且电感电流有效值显著增加，使得变换器的损耗增大，效率明显降低．所以本文只针对模式1、4、5进行有效分析，根据1.3节中标幺化电感电流有效值平方和标幺化传输功率表达式得到1、4、5工作模式的标幺化电感电流有效平方值和标幺化传输功率值Pn,t．

通过减小电感电流有效值，以此减少DAB变换器的开关损耗，提高变换器的传输功率，来达到提升整体变换器传输效率的目的，因此就需要对电感电流最小值的实现进行研究．

2 电流有效值优化过程

前面已经分析出模型的传输功率和电感电流与三个移相比之间的函数关系，现在在高中低功率下分析一种可以求解电感电流最小且提高传输功率的优化方法．

2.1 优化方程推导

求解电感电流有效值的最小值，首先要求出D1，D2，D3的扰动对和Pn,t的影响，这样才能得出最优控制点．和Pn,t对于控制变量D1，D2，D3的微分表示为

式(9)(10)描述了变化的D1，D2，D3对于和Pn,t的影响，现可以用一个具体的评价指标ξ来描述，则

对于模式1、4、5来说只要满足下列等式关系即可实现该模式下电感电流有效值最小

即满足控制变量(D1，D2，D3)下的评价指标相等就能得出最优的控制点．

2.2 工作模式1的最优控制

范围是第二个区域Pn,t范围是

由于功率有效值区间分别位于整个传输功率的中端和高段，因此称第一个Pn,t区域范围内的解为中等功率范围解．第二个Pn,t区域范围内的解为大功率范围解．

中等功率区域范围优化方程的解为

在工作模式1内D1的取值范围为

设电压变比M=0.7，再将(D1，D2，D3)代入工作模式1的电感电流公式，分别取D2=0，0.1，0.2，计算得出任意D1、D3时，的值在工作模式1的定义域内是随D2的增加而单调递增的，因此取得最小值时D2最小为0．M=0.7时，通过式（15）计算得到(D1，D2，D3)的结果与计算的理论结果如表2所示．

表2 中等功率下理论结果和计算结果的比较Tab 2 Comparison of theoretical results and calculation results under medium power

优化方法计算的结果与理论结果完全相等，所以式（15）在工作模式1范围内完全是可行性的，该方法成立．

在该模式下，当Pn,t进一步增大至1的区域范围内，也就是大功率范围内，优化方程的解为

计算得到D3的范围为

从三移相优化控制计算的结果可以看出在大功率范围下的最优控制就是传统的单移相控制，也就说明在大功率范围下单移相控制即可满足电感电流有效值最小．

2.3 工作模式4和5的最优控制

将(D1，D2，D3)代入工作模式4和5的电感电流优化方程．区域范围下优化方程的解为

由上述解可以推导出在工作模式4和5范围下解（D1，D2，D3）始终满足D1=D2+D3的关系，这是因为模式4和5定义域相交的区域是D1=D2+D3的平面，所以模式4和5区域范围下的解一定相同，并且在共同的交集面上，优化方程的解满足的关系式也说明了该优化控制方法是可行的．

在工作模式4和5内(D1，D2，D3)的取值范围为

得出

由上式的Pn,t范围可以看出式（19）是小功率下的解．

取M=0.7，通过式（19）计算出(D1，D2，D3)的结果与计算的理论结果来验证此控制策略的可行性，结果如表3所示．

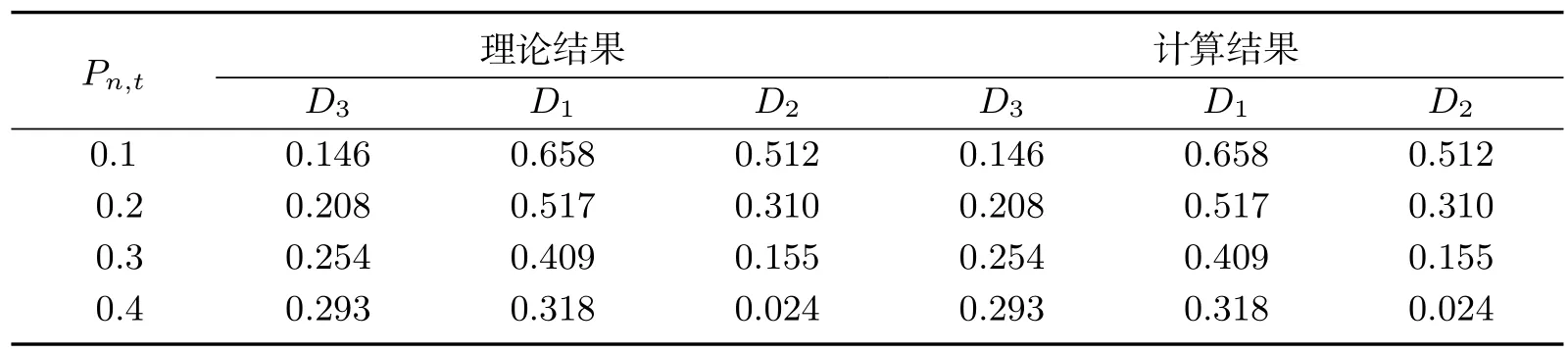
表3 大功率范围下理论结果和计算结果的比较Tab 3 Comparison of theoretical results and calculation results under high power range

表（3）结果表明利用式（19）计算出得到(D1，D2，D3)的结果与数值计算的理论结果完全相同，因此该控制方法在模式4和5内可行．

3 仿真分析

由DAB的拓扑结构以及高中低功率下的最优控制参数分析结果，在MATLAB上搭建仿真模型，由于在大功率范围下单移相控制可实现电感电流最小，因此只需要对小功率和中功率范围下，分别使用单移相控制和三移相优化控制进行仿真以验证文中优化控制的可行性，主要参数如表4所示．

表4 仿真电路参数数值Tab 4 Simulation circuit parameter values

首先，在一次侧直流电压200 V，二次侧直流电压140 V，变压器匝数比为1：1，M=0.7条件下进行仿真，此时Pn,t=0.2，在小功率范围下进行仿真对比．图6是根据工作模式4和5在三移相优化控制的优化控制参数下所得到的仿真波形，此时D1、D2、D3均大于0，转换器二次侧全桥相对一次侧全桥进行移相，两个全桥内部两两开关管之间也进行移相，分别得出一二次侧交流输出电压以及电感电流值．图7是根据单移相控制所得到的仿真波形，此时只有二次侧全桥相对一次侧全桥进行移相，两个全桥内部两两开关管之间无移相，分别得出一二次侧交流输出电压以及电感电流值．从结果可以看出，三移相优化控制的电流峰峰值从单移相控制的19.5A下降至三移相优化控制的15.5 A，通过计算得出在该功率点下电感电流有效值从单移相控制的4.6A下降至三移相优化控制的3.5 A．

图6 小功率范围下三移相优化控制仿真波形Fig 6 Triple phase shift optimization control simulation waveform in a small power range

图7 小功率范围下单移相控制仿真波形Fig 7 Single phase shift optimization control simulation waveform in low power range

接着在一次侧直流电压200 V，二次侧直流电压140 V，M=0.7，Pn,t=0.6条件下，即在大功率范围内进行仿真对比．图8是根据工作模式1三移相优化控制的优化控制参数下所得到的仿真波形，此时D1和D3大于0，D2=0，转换器二次侧全桥相对一次侧全桥进行移相，一次侧全桥内部两两开关管之间进行移相，二次侧全桥内部两两开关管之间无移相，分别得出一二次侧交流输出电压以及电感电流值．图9是运用单移相控制所得到的仿真波形，分别得出一二次侧交流输出电压以及电感电流值．从结果可以看出，三移相优化控制的电流峰峰值从单移相控制的27.2 A下降至三移相优化控制的25 A，通过计算得出在该功率点下电感电流有效值从单移相控制时的7.4 A下降至三移相优化控制时的7.0 A．

图8 中功率范围下三移相优化控制仿真波形Fig 8 Triple phase shift optimization control simulation waveform in the middle power range

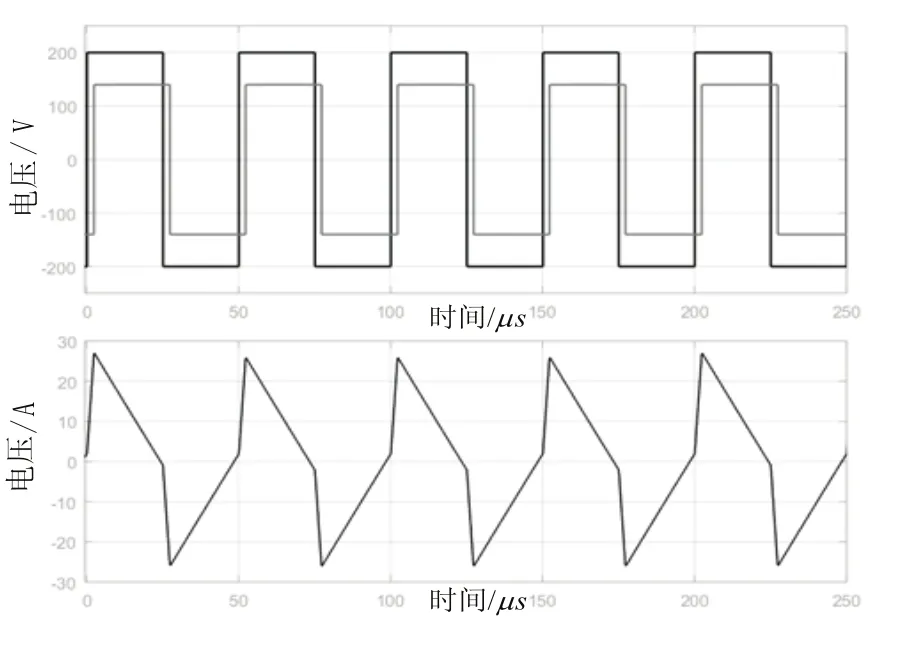
图9 中功率范围下单移相控制仿真波形Fig 9 Simple phase shift optimization control simulation waveform in the middle power range

从以上Pn,t=0.2和Pn,t=0.6两组结果可以看出，在低中功率范围下三移相优化控制都分别降低了转换器中的电感电流有效值和峰峰值，图10显示不同传输功率下变换器的转换效率，可以看出三移相优化控制策略下最大转换效率可达98.2%，所以实验结果表明该三移相优化控制策略在低中功率范围内相对于单移相控制策略有效降低了电感电流有效值，从而电路转换效率得到提高．

4 结论

本文根据双有源桥DC/DC变换器的三移相控制，以减小电感电流有效值的目标来提高变换器的功率传输效率，将变换器电路结构等效为两个交流方波电压和一个电感串联的等效电路，并对电压电流进行分解，得出变换器的电压电流功率表达式，根据三个控制分量D1、D2、D3存在的六个范围给定三个有效工作模式，以电感电流有效值最小和提高传输功率的目标建立优化方程进行分析推导优化方程，将三种工作模式的电流有效值和传输功率根据优化方程条件，推导出不同传输功率段下电流有效值的优化控制条件，得到高中低功率范围下三移相优化控制的优化参数．最后通过仿真结果表明，在中低功率范围下三移相优化控制策略能减小电流峰峰值及有效值，提高了变换器的转换效率，验证了该三移相优化控制的可行性．

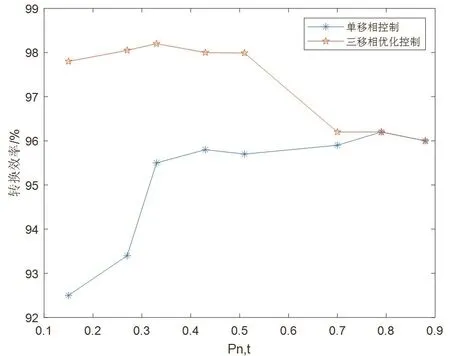
图10 三移相优化控制与单移相控制转换效率对比曲线Fig 10 Comparison curve of conversion efficiency with triple phase shift optimization control and single phase shift control