基于多智能体系统仿真的最短路径规划
唐 勇, 何东林, 朱新平
(1.成都大学 信息科学与工程学院, 四川 成都 610106;2.中国民航局第二研究所 科研开发中心, 四川 成都 610041;3.中国民用航空飞行学院 空中交通管理学院, 四川 广汉 618307)
0 引 言
最短路径规划是图论与网络规划中的经典问题,广泛应用于基于地图信息的交通导航、车辆调度管理、航线航路规划、市政交通规划以及网络通信路由选择等领域[1-4].对此,科研人员对最短路径规划问题进行了大量研究[5-7],并提出了一系列最短路径算法及各种改进算法,比如,A*算法、Dijkstra算法、Floyd算法、Bellman-Ford算法及SPFA算法等[8-12].总体来看,现有的最短路径算法大多利用数学分析方法实现,但也存在解析参数过多或难以确定,甚至解析解不存在的情况.针对此问题,科研人员提出了系统仿真法对复杂系统进行求解,并取得了较好结果[13].基于此,本研究利用多智能体系统设计了最短路径仿真算法,把有向图中的节点与边都建模成智能体,再设计机器人智能体,利用机器人智能体的自我复制和移动能力,让机器人智能体沿着节点出边对与该节点相连接的节点进行并行移动访问,从而快速实现对有向图节点的遍历,采用系统仿真运行的方式直观地获取有向图最短路径.
1 问题描述
在具体应用中,实际的最短路径问题通常转换为权重有向图.设权重有向图,G=(V,E),这里V为G中的顶点集合,E为G中的边集合.设有向图G的权重函数为w:E→R,即权重函数w把G中的每条边映射为实数域中的数值,于是,某条路径,p=〈v0,v1,…,vk〉,的长度可以用构成该路径的全部边的权重值相加得到,
(1)
因此,从节点a到节点b的最短路径可以用最小权重函数进行表示,

(2)
边的权重既可以是实际道路的几何距离,也可以是其他度量单位,如时间、流量和成本等与路径长度线性增加的量.
此外,最短路径问题也可以分为指定结点间的最短路径、单目的地最短路径及所有节点间的最短路径.指定节点间最短路径,即计算给定的2个节点之间的最短距离;单目的地最短路径,即计算所有节点到目的地节点的最短距离;所有节点间最短距离,即计算任意2个节点之间的最短距离.单目的地最短路径和所有节点间最短路径都可以归结为指定节点间最短路径的扩展.
本研究只研究指定节点间最短路径,即:设有如图1所示的有向图,各条路段上的数字标明该条路段的长度(这里设路段权重数值都为正),求从P1到P6的最短路径.
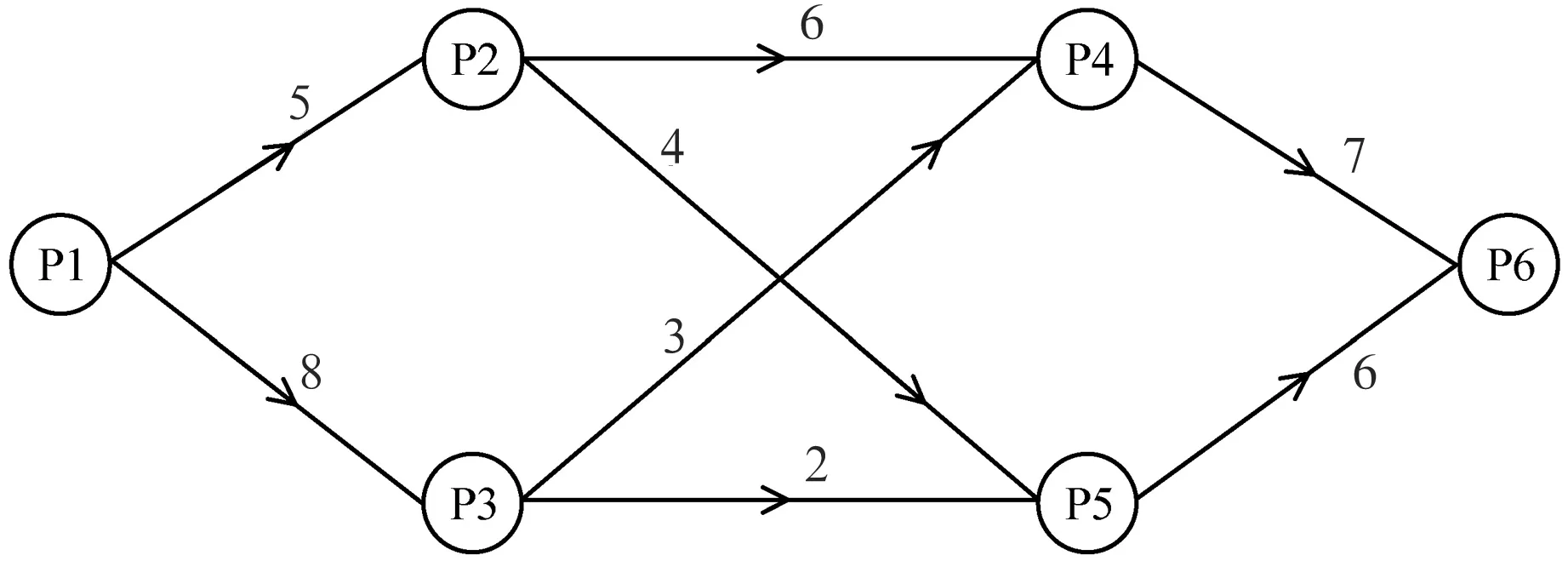
图1最短路径有向图模型
2 系统设计
2.1 系统结构设计
根据定义,多智能体系统中的每个智能体都具备独立自主能力,每个智能体都选择最有利于个体利益的策略.由于多智能体系统存在多个智能体,各个智能体在选择最有利于自己的策略时必然产生冲突.对此,多智能体系统的目的是实现系统的整体利益最大化,此时就需要在各个智能体之间进行沟通和协调,让个体利益服从整体利益.由此可见,智能体个体功能的设计和智能体之间的协调机制的确定是多智能体系统设计的关键.同时,根据不同的规划目标选择合适的系统结构是实现多智能体系统的重要保证.根据计算最短路径的需求,本研究设计的层次型多智能体系统结构如图2所示.
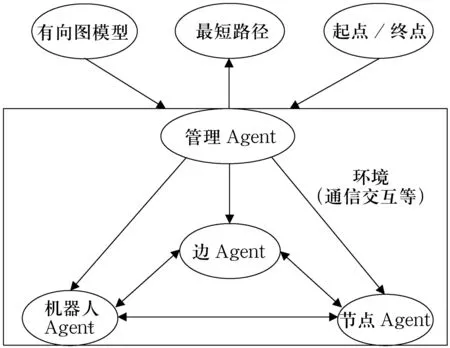
图2层次型多智能体系统结构
图2所示系统中,管理Agent负责多智能体系统的运行控制,是系统的关键智能体;节点Agent对应于有向图中的节点;边Agent对应于有向图中的边;机器人Agent是系统中的移动智能体,负责完成从起点到终点的运动;环境是多智能体系统的运行后台,负责提供和管理系统运行的基础功能,比如消息传递与智能体连接关系等;起点和终点节点对、有向图均是系统的输入信息,最短路径是系统的输出信息.
2.2 Agent设计
2.2.1 管理Agent.
管理Agent担负系统的管理功能,负责整个多智能体系统运行控制,获得路径规划结果.管理Agent在多智能体系统启动时首先完成初始化工作,根据系统输入的有向图设置节点Agent和边Agent,根据起点和终点产生第一个机器人Agent(初始机器人Agent),并放入起点对应的节点Agent(初始节点Agent).同时,对各种Agent的相互协作提供运行管理支持,输出最短路径.
2.2.2 节点Agent.
节点Agent对应于有向图的节点,是供机器人Agent进行自我复制和边断开操作的环境.节点Agent具有名称和出入边属性.其中,名称即是节点Agent的编号,可对节点身份进行标识;出入边属性标识了该节点Agent的出边和入边数量以及与边Agent的关联关系等.
2.2.3 边Agent.
边Agent对应于有向图中的边,边Agent具有时间属性、方向属性及节点关联属性等.时间属性对应于有向图中的权重,指明了机器人Agent通过该条边所花费的时间;方向属性指明了机器人Agent在边Agent上的运动方向;节点关联属性指明了边Agent与节点的关联关系,即有向图中节点间的连接情况.
2.2.4 机器人Agent.
机器人Agent具有节点间移动能力、自我复制能力、边断开能力及历史节点属性.机器人Agent会沿着某个节点Agent出边的方向移动到其下个节点Agent,移动的时间等于边的权重值.
如果节点Agent有不止一条出边,则机器人Agent能自我复制出多个机器人,即让该节点Agent的每条出边都由机器人Agent占据.机器人Agent只有在到达节点Agent且该节点Agent有不止一条出边才立即进行自我复制.若节点Agent有n条出边且n>1,则自我复制的数量为(n-1).如果节点Agent有多条入边,机器人Agent到达该节点后只留下它曾走过的入边,而把其他入边都断开(确保任何节点至多被访问一次).历史节点属性记录该机器人已通过的节点,以便最后输出路径.一旦有机器人Agent到达终点,便完成最短路径计算过程.该机器人Agent走过的路径即是从起点到终点的最短路径,则系统输出最短路径,结束多智能体系统运行.
2.3 多智能体系统运行过程
最短路径多智能体系统运行过程是机器人Agent通过在边Agent上的移动和自我复制实现对节点Agent遍历最终获得最短路径的过程,具体为:系统运行开始后,第一个机器人Agent出现在起始节点Agent处,根据起始节点出边数量决定是否自我复制,并沿着出边Agent移动到相邻节点Agent;当有机器人Agent移动到目的地节点Agent,系统就完成了对有向图中最短路径的计算,停止系统遍历,输出机器人Agent走过的节点即得到最短路径.
在系统运行过程中需注意的是:第一个机器人Agent根据系统提供的有向图、起点及终点/节点选择活动初始点;机器人Agent只在边Agent上移动才耗费时间,耗费的时间等于边的权重,通过节点Agent和自我复制不会耗费时间;由于机器人Agent对节点Agent入边的断开能力,保证了任何节点最多被访问一次而不会出现环路.
3 算法测试
3.1 算法测试
本研究选择Anylogic 8.2作为开发平台,进行最短路径规划多智能体系统开发.Anylogic是目前最专业的多Agent系统(Multi-agent system,MAS)开发工具,也是目前最成功的MAS系统商业开发平台.Anylogic提供了各种Agent控件及多智能体系统需要的通信交互等功能,让开发者把主要精力用于设计算法的实现上,有效降低了多智能体系统的开发难度.
本研究以图1所示的有向图对最短路径多智能体系统进行算法测试:设P1为源节点,P6为目的地节点,求P1到P6间的最短距离.
最短路径规划多智能体系统的运行初始界面如图3所示,图4~图6中缺失的边即是系统运行过程中被机器人Agent到达节点Agent后断开的入边Agent.边Agent被断开后,在其上运动的机器人Agent会一并消失.图4中,由于从P2来的机器人Agent先到达P6,因此(P3,P5)边被断开.图5中,从P2来的机器人Agent先到达P4,于是(P3,P4)边被断开.图6中,从P5来的机器人Agent先到达P6,于是(P4,P6)边被断开.由于P6是终点,系统便停止运行,输出最短路径为P=〈P1,P2,P5,P6〉,最短路径长度为15.本研究通过最短路径规划多智能体系统,让最短路由计算过程完全可视化,通过系统仿真的形式获得了指定节点对之间的最短路径,形象直观展示了整个系统的运行过程.
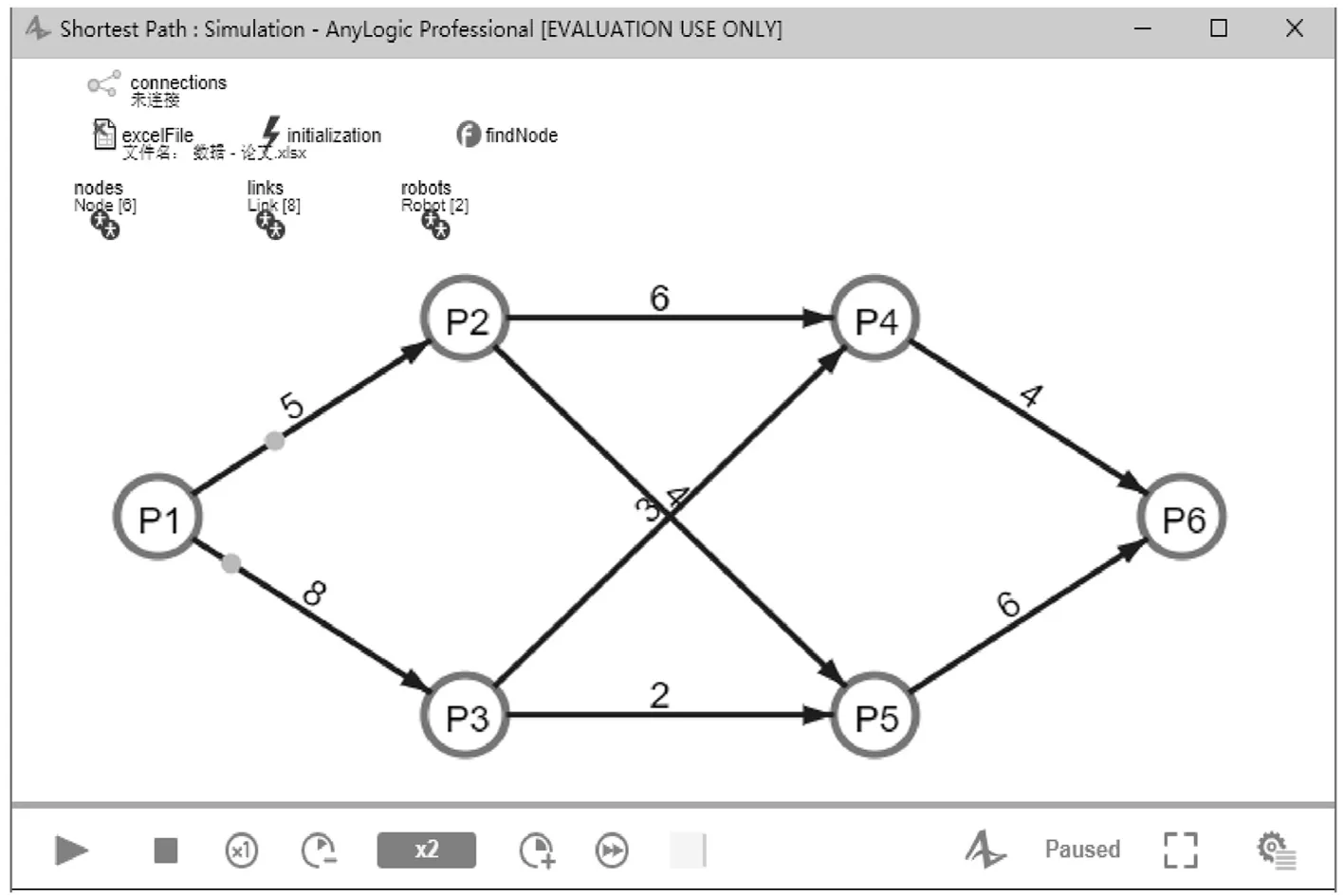
图3 MAS最短路径启动界面
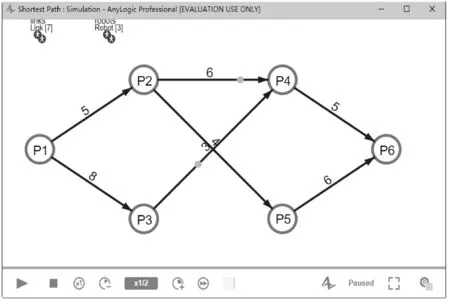
图4边(P3,P5)被断开
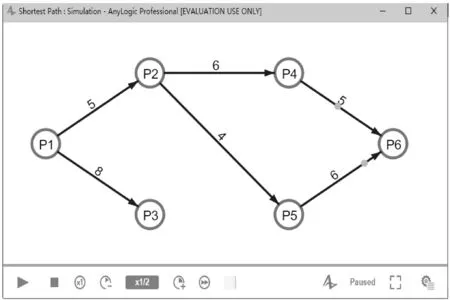
图5边(P3,P4)被断开
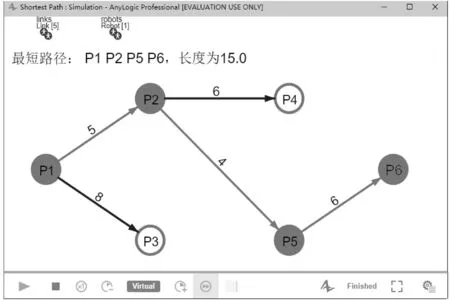
图6机器人Agent到达节点P6,边(P4,P6)被断开,仿真结束
3.2 算法复杂度
假设有向图共有E条边,由于每条边最多有一个机器人Agent通过,所以机器人Agent的最大复制次数为E.每次复制机器人时,算法需要把它走过的节点添加到新复制的机器人历史节点属性中,最大添加次数为V.因此,最短路径多智能体系统的算法复杂度不超过O(VE),此与Bellman-Ford算法复杂度相同[11].
4 结 语
本研究利用多智能体系统实现了单源最短路径计算,不同于传统的最短路径算法,本研究算法通过Agent的移动、复制和相互协同实现对有向图节点的遍历,快速找出了从源点到目的地的最短路径.本研究把边的权重转换为机器人Agent通过该条边所花费的时间,利用Anylogic进行系统开发,通过机器人Agent在有向图中的移动直观展示了系统寻找最短路径的过程,使得整个运行过程直观可视.同时,本研究通过多智能体系统中各种智能体功能、属性和协调等的定义和设置,使得任何边最多被访问一次,有效控制了算法复杂度不超过O(VE).需说明的是,由于机器人Agent的运动时间不能为负数(或者移动速度不能为负),因此本研究算法不能对包含负值权重的有向图求最短路径.

