例谈三角恒等变换的几种技巧
2019-08-26 08:28祁花菊
数理化解题研究 2019年22期
祁花菊
(河北省石家庄市第十七中学 050000)
一、变公式
三角恒等变换是以同角关系,诱导公式,和、差、倍角等公式为工具的,重在变什么、怎么变的问题,所以我们首先要熟悉各个公式在恒等变换中的作用,在此基础上还要学会公式的变式运用,这是实施三角变换最基本的技巧.
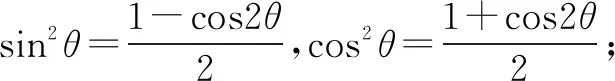
(2)求函数f(x)=4cos22x-3sin22x的最小正周期.
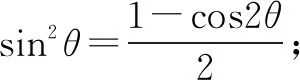

变式训练1若函数f(x)=cos2ωx+3sin2ωx的最小正周期是1,求ω的值.
二、变常数






三、变角度
运用转化“角”的技巧,无疑应该放在转化角、名、次、式等常用技巧的第一位,因为千变万化先看角的变化,一个命题中角与角之间必有联系,如条件与条件、条件与结论、结论与结论之间角的差异,一旦联系起来,便明白向哪个角转化了.






四、变名称
运用转化“名”的技巧也应并驾齐驱,当几种三角函数共存时,我们就应该考虑是切化弦、弦化切,还是弦化弦的问题.
例4 求sin40°(tan10°-tan60°)的值.
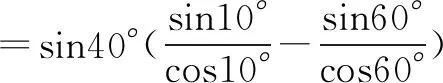
点评注意求值题是一类重要题型,给角求值时常用切化弦、弦化弦的策略,并注意所给角要向特殊角或基本角转化,如本题中的基本角是10°.
变式训练4求sin50°(1+tan60°tan10°)的值.
五、变次数
运用转化“次”的技巧也不能等闲视之,当有了次数太高或要开方等信息时,我们便要考虑是降次、升次,还是平次转化的问题.

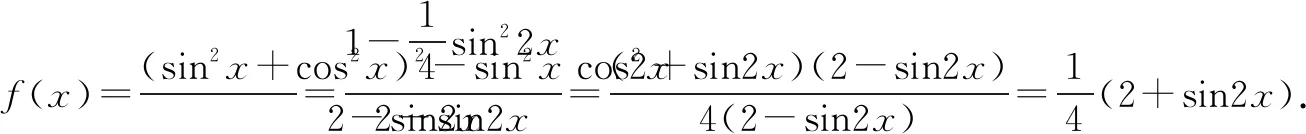

点评注意配方、分子分母同乘、因式分解等是恒等变换的重要策略,如本题用了这些策略后,既降了幂又化了分式为整式,何乐而不为!

六、变结构
运用转化结构“式”的技巧更是至关重要,如条件式与条件式、条件式与结论式、结论式与结论式之间的信息,一旦联通起来,便可融为一体、相互协作了.
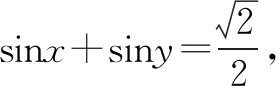
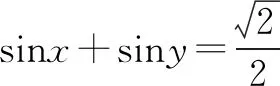

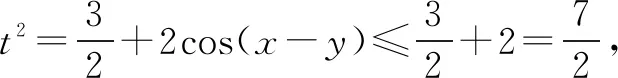

点评注意换元的策略,既把三角问题转化为代数问题来解决,还有平方后再相加等策略,使之依靠整体的力量,以真正起到事半功倍的效果.
猜你喜欢
中等数学(2022年7期)2022-10-24
中学生数理化·高一版(2021年1期)2021-03-19
中学生数理化·七年级数学人教版(2020年12期)2021-01-18
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
新高考·高二数学(2017年9期)2018-03-16
中学生数理化·七年级数学人教版(2017年3期)2018-01-20
求学·理科版(2016年11期)2016-11-29
小猕猴智力画刊(2016年5期)2016-05-14
幼儿智力世界(2016年8期)2016-05-14
幼儿智力世界(2015年5期)2015-08-20

