售电公司最优购电模型研究

李德智, 袁伟伟，2

(1.中国电力科学研究院有限公司， 北京 100192； 2.华北电力大学， 北京 102206)

0 引言

在新电改背景下，售电公司需要实现购电组合优化，来达到收益最大化的目标，以适应新形势下的市场竞争。售电公司能够参与竞价购电的电力市场包含长期合约市场、短期日前市场和实时现货市场。从期望效益最大的角度来看，每一个市场的电价水平不同，并有一定的波动区间，对于售电公司而言分别适用于不同的配售电情景，售电公司需要分配好在这3个市场中的购电组合，以达到购电成本最低，收益最高。从减小风险的角度看，在分配市场购买电量的同时，由于电能商品的不可存储性，会给售电公司购电带来一定的不确定性。如何在3个市场中合理分配电量，同时降低风险损失和风险成本，形成科学的购电组合方案，是售电公司需要面对的重要问题之一。

目前国内对发电侧售电策略、供电侧售电策略的研究相对较多，而供电侧购电策略的研究仍处于起步阶段。文献[1]引入了投资组合理论，修改并完善了其中的 Markowitz模型。文献[2]提出了衡量配电侧最优购电分配的评价指标。文献[3]运用了条件风险价值方法对各个类型的市场进行了组合计算。文献[4]利用Monte-Carlo基因算法模拟并求解了购电策略问题。文献[5]对发电企业的最优竞价策略问题和大用户直购电市场环境下的最优购电策略问题分别进行了研究。

国外对于购电行为的研究主要着眼于用户向供电侧购电，并偏好基于具体的电力市场环境、市场性质，对购电过程进行模拟和分析。文献[6]建立了适合台湾发电企业的煤炭购买证券投资组合模型。文献[7]试图确定供电企业的受保障能源购买价格。文献[8]优化了电能配送过程中的电力以及可再生能源的证书购买过程。文献[9]提出了适用于大用户直购电的多状态电价模型。文献[10]分析了阶梯式购电的可行性。

本文在以往研究的基础上，考虑了售电公司风险偏好相异的不确定性，并提出各个售电公司根据不同市场价格波动进行选择的分级优化模型。首先对售电公司的价格波动响应进行分析，构建以购电成本最小为目标的各公司分市场购电优化模型，并依照模型得出的方案进行比较和排序；其次，基于不同公司对交易市场电能价格波动的不确定性响应，采用了区间法构建了售电公司的风险概率和风险损失评估模型，依据历史数据确定价格波动的区间，并根据供电公司的风险偏好对公司进行分类、确定不同价格下的弹性系数，并利用建立的风险损失评估模型求解最优方案。

1 一级模型：各售电公司分市场购电响应模型

假设第i类售电公司在交易市场电价波动前的电价为Pio，设长期合约市场为市场1，短期提前市场为市场2，实时现货市场为市场3；第i类售电公司的市场1电价为Pi1、市场2电价Pi2、市场3电价Pi3不变；售电公司的购电市场主要分为市场1、市场2、市场3，因此我们假定第i类售电公司的购电响应矩阵为三阶矩阵，如式(1)。

(1)

其中，εi,11,εi,22,εi,33为第i类售电公司在某市场的电价变化率所带来的该市场购买电量的变比率。εi,12,εi,13, … ,εi,23为第i类售电公司在某市场的电价变化所带来的其它市场的购买电量变化率。对式(1)进行转化，可以得到某市场第i类售电公司经历电价波动后在各市场的购电量如式(2)。

(2)

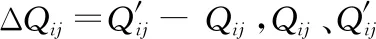
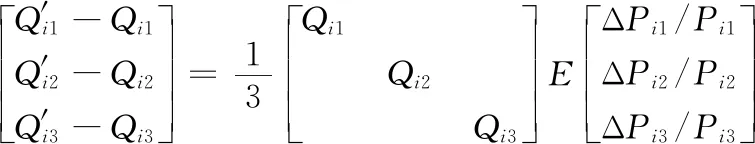
(3)

在实际情况下，各类售电公司的风险偏好不同，面对的选择境地不同，售电公司的购电响应具有不确定性。假设售电公司购电响应矩阵具有一定的随机性，将其视为随机变量，采用区间法解决该问题。

不同的售电公司对于各个市场的依赖程度有所不同，喜好风险的售电公司可能会在市场2、市场3中增加购买量，而厌恶风险的售电公司则会更多地购买市场1的电量。假定存在风险偏好系数ki，事实上，风险偏好系数ki与电价需求弹性系数εi,kj有相关关系，对各个市场的电量购买偏好直接影响电价需求弹性系数εi,kj。可以用εi,kj代表第i类售电公司的风险偏好。

设每类售电公司的响应矩阵中的电价需求弹性系数εi,kj=[εi,kj,εi,kj]={εi,kj|εi,kj<εi,kj<εi,kj},εi,kj和εi,kj是确定的区间数。假设εi,kj服从N(ui,kj，σ2i,kj)正态分布，根据“3σ准则”，得到式(4)、式(5)。

ui,kj=Mid(εi,kj)

(4)

σi,kj=Len(εi,kj)/6

(5)

其中,Mid(εi,kj)表示区间数εi,kj的中间值,Len(εi,kj)表示区间的长度。于是，售电公司在经历市场购电价波动后，在各市场增加的购买电量的期望值为式(6)。

Qi1Ei(εi,12)ΔPi2/Pi2+Qi1Ei(εi,13)ΔPi3/Pi3]

(6)

售电公司在市场价格波动前的购电成本为π1,如式(7)。

π1=Qi1P01+Qi2P02+Qi3P03

(7)

售电公司在一次市场价格波动后、各市场购买电量不变动的购电成本为π2，如式(8)。

π2=Qi1P11+Qi2P12+Qi3P13

(8)

则市场电价变动后，售电公司的总购电成本变化为式(9)。

(9)

则分市场售电公司购电优化模型追求的目标函数应为，总购电成本最小化，如式(10)。

通过上述的成本最小目标，根据历史数据，可对分市场购电方案作进行排序，以得出最佳方案。

2 二级模型：售电公司风险概率计算

弹性系数与价格的绝对值有关。可以对售电公司购买电价的历史数据进行分析，并划定一定的变化范围。

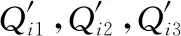
其中，Δπ-=minΔπ，Δπ+=maxΔπ，购电成本变动Δπ为区间数，区间长度代表购电成本波动范围，区间长度的长短，代表了售电公司购电成本变动的不确定性高低。

若Δπ-<Δπ+<0，则说明售电公司重新分配市场购买电量后的成本收益是正的，即购电响应措施可行；

若0<Δπ-<Δπ+，则说明售电公司重新分配市场购买电量后的成本收益是负的，即购电响应措施不可行；

若Δπ-<0<Δπ+，则说明Mid(Δπ)的符号不确定，即购电响应措施的可行度承担一定风险。

根据正态分布的性质,可以得出Δπ也服从N(u1,σ21)的正态分布，根据“3σ准则”，可以得出式(12)、式(13)。

u1=Mid(Δπ)

(12)

σ1=Len(Δπ)/6

(13)

其中,u=Mid(Δπ)表示区间数Δπ的中间值,Len(εi,kj)表示区间的长度。引入风险概率的计算方法，如式(14)。

(14)、

Pr即为售电公司购电响应的风险概率。

令Pr<ɑ，根据一级模型进行方案排序，并按次序代入至风险概率模型，与ɑ对比检验，若不符合要求，则进行下一个方案的代入，直到满足条件为止，如图1所示。

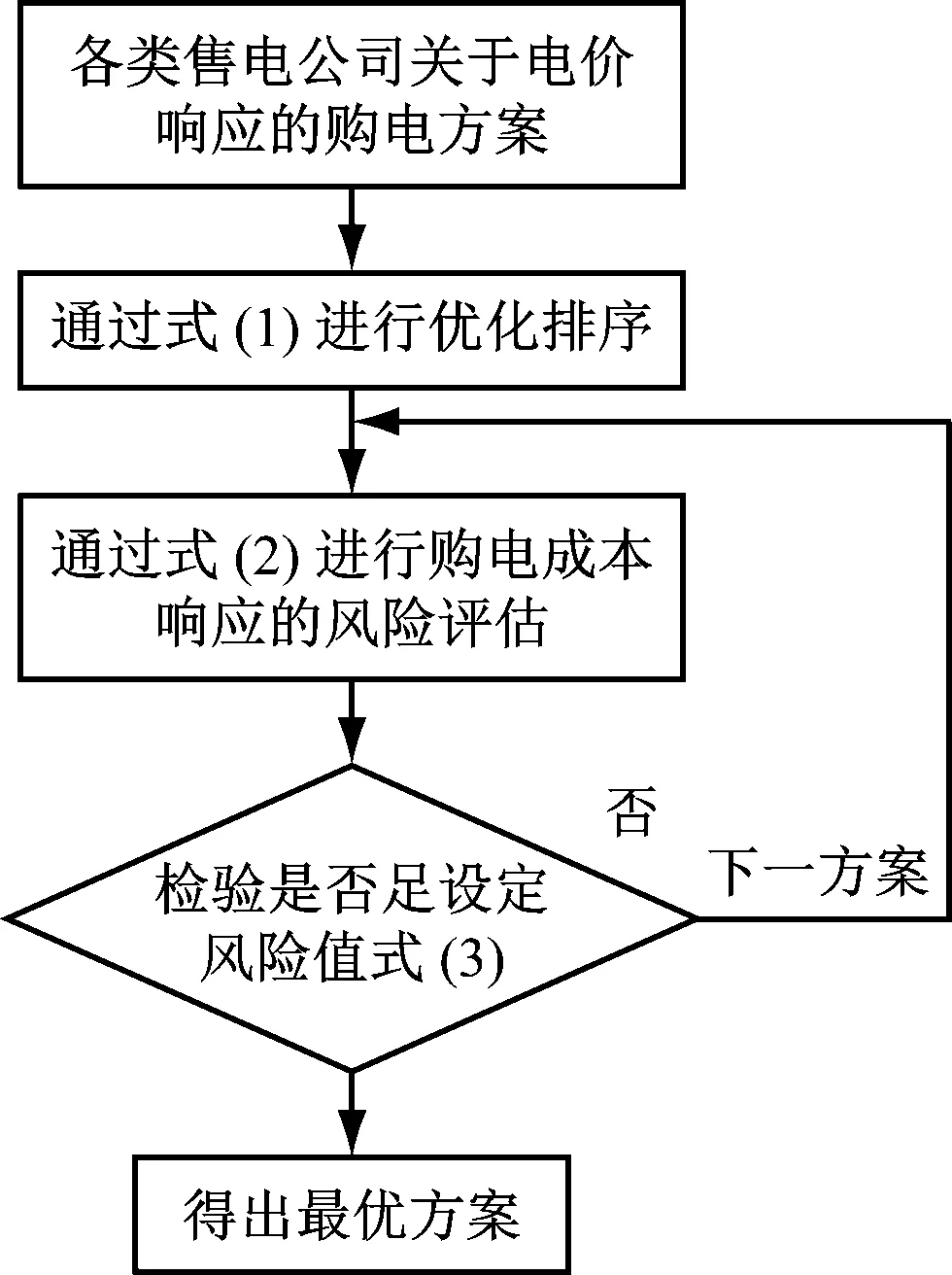
图1 方案筛选流程

3 算例分析

本研究将售电公司分为风险偏好型、风险中性、风险厌恶型三种类型。以往的研究显示，风险偏好型售电公司在实时现货市场的购买量相对风险厌恶型企业则较多；风险厌恶型售电公司在对未来电量进行预测时会保留一部分富余电量，在长期合约市场和短期提前市场的购买电量占比较大。本文采集了某典型地区3家不同风险偏好的售电公司分别在市场1、2、3的日购电量及总购电量，如表1所示。

采用某区域电力市场的电价数据，如表2所示。

根据发电企业在电力市场实行电价的历史数据以及售电公司的历史购电数据，代入弹性矩阵，可以求出每个弹性系数的最大值和最小值。于是每类售电公司响应矩阵的区间数，如表3所示。

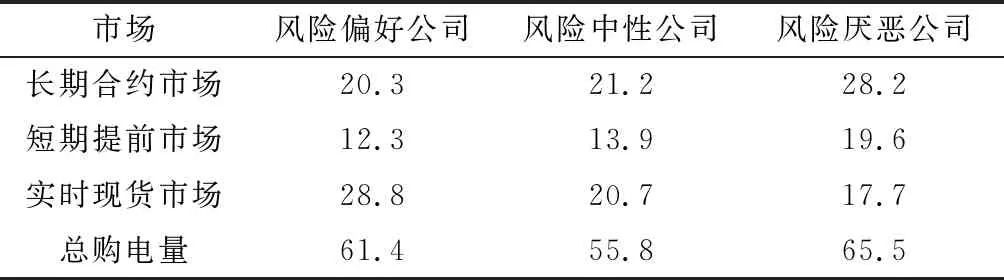
表1 各类售电公司分市场日购电量(MWH)

表2 分市场电价表

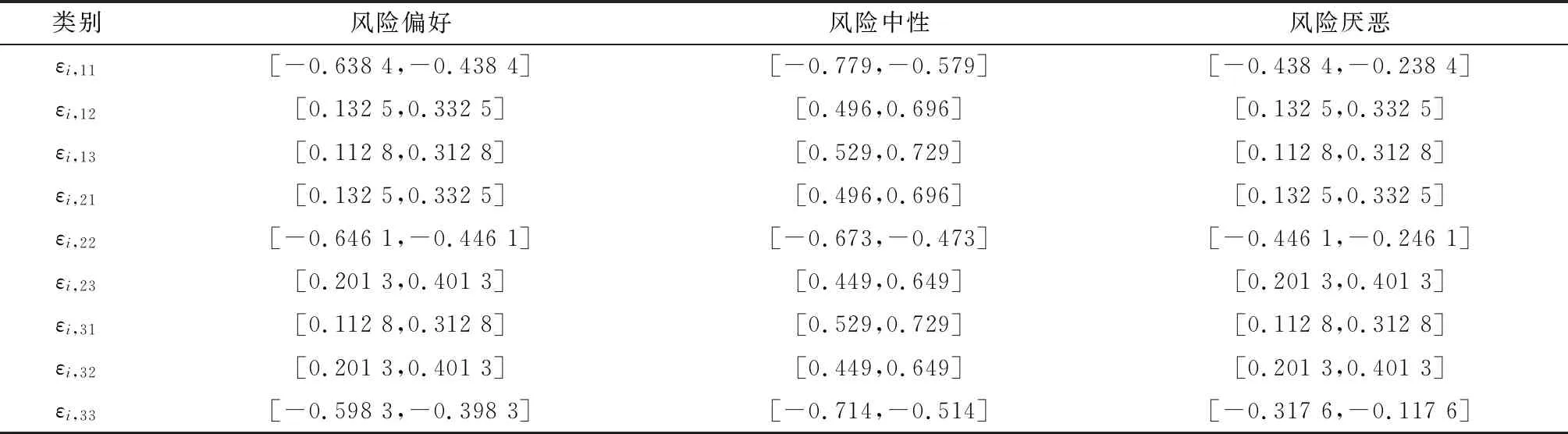
表3 各类售电公司的电价需求弹性系数的区间数

在未来电量科学预测的基础上，各类售电公司对于各电力市场的电价水平波动进行响应的购买量存在一定的变化范围。对3类售电公司的购买量变化幅度进行排列组合即可得到售电公司购买响应方案。风险偏好型公司对于市场1和2的价格响应较为迟缓一些，变化范围相对小一些，对于市场3的价格响应较为敏感一些，变化范围相对大一些；风险厌恶型公司对于市场1和2的价格响应较为敏感一些，变化范围相对大一些，对于市场3的价格响应较为迟缓一些，变化范围相对小一些。具体见方案如表4所示。

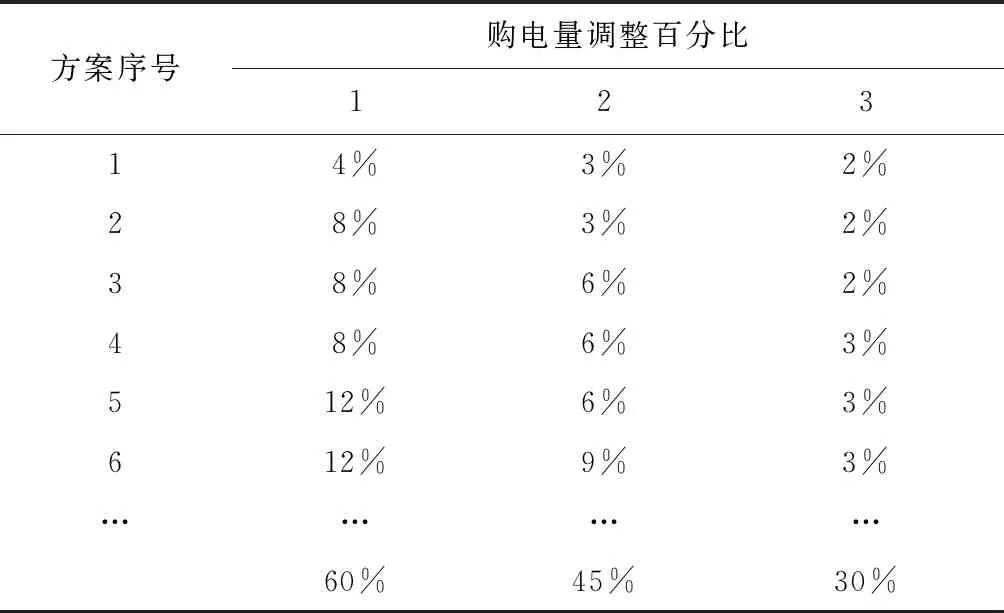
表4 电量购买方案

通过建立的一级模型，可以求出成本最小目标的最优方案，如表5所示。

表5 目标函数下的最优方案

根据目标函数以及概率函数得出结果，如表6所示。

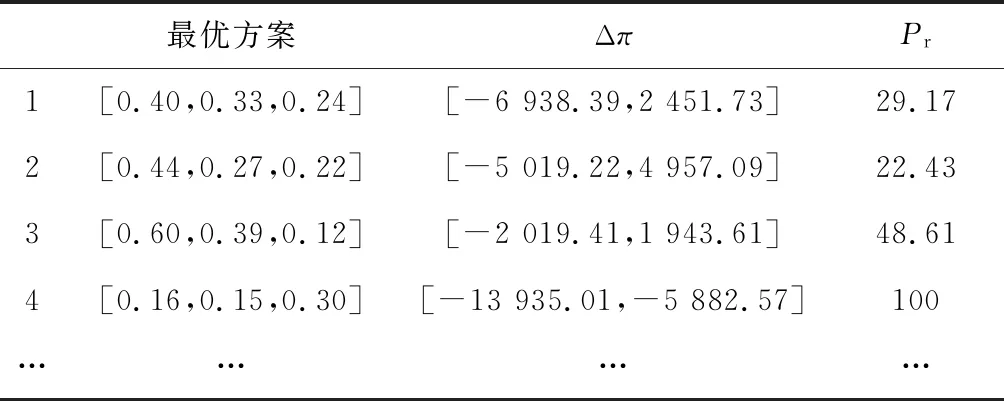
表6 最优结果

从算例结果分析来看，方案1可以实现购电成本最小目标，但是风险概率的高企显示，如果实行方案1的购电方案，购电成本的不确定性会增加，为本就不确定的电量供应和电量需求增加风险。综合来看，方案2既可以使得购电成本尽量降低，售电公司在购电市场承担的风险也相对较小。

4 总结

本文基于售电市场放开的大背景，对售电公司的最优购电方案问题进行了研究和模拟计算，试图优化我国电力市场中售电侧交易主体的购电行为，得出的结论如下。

(1)售电公司作为交易主体在电力市场进行购电时，具备一般消费者的通性，即追求成本最低、风险最小。基于3种主要的购电交易市场、对售电公司的风险偏好进行分类研究具有一定的实际意义。

(2)购电市场的电价波动将影响各个售电公司的购电策略，并受到各售电公司风险偏好不同的影响。使得购电成本最低的购电策略不能保证售电公司承担的购电风险同时处于低水平。需要同时计及购电成本最低和购电风险最小双目标，以得到售电公司购电的优化模型。

(3)区间法的使用适用于购电响应分级优化模型的建立和求解。其中有一些不足之处仍有待进一步研究：第一，未将发电企业在售电市场的动态定价考虑在计算模型中；第二，没有加入因时节变化、时段变化而导致电量供需变化的变量和参数；第三，因缺少实际数据，对售电公司的分类还有待进一步细化。